- Как определить кратность числа в Python: основные способы проверки
- Что такое кратность числа
- Как найти кратность числа
- Метод деления с остатком
- Метод умножения на целое число
- Как проверить кратность числа в Python
- Оператор деления по модулю
- Операторы сравнения
- Как проверить кратность числа в одну строку
- Практические примеры
- Видео по теме:
- Вопрос-ответ:
- На чём основано определение кратности числа в Python?
- Как можно проверить кратность числа 7 в Python?
- Можно ли проверить кратность числа сразу для нескольких чисел?
- Какая функция в Python позволяет проверить кратность числа?
- Могут ли отрицательные числа быть кратными?
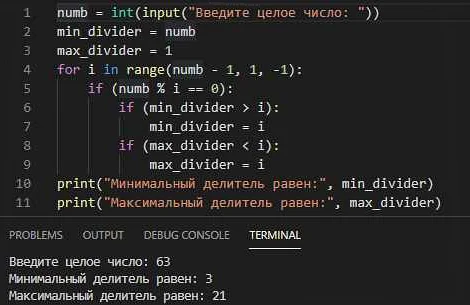
- Как можно определить все делители числа в Python?
- Можно ли использовать оператор деления для проверки кратности числа?
Как определить кратность числа в Python: основные способы проверки
Узнайте, как легко проверить кратность числа в Python с помощью оператора % и условного оператора if. Примеры кода и объяснения шаг за шагом для удобства понимания.
Язык Python пользуется огромной популярностью в сфере программирования благодаря своей простоте и удобству. Один из важных аспектов в работе с числами в Python – это проверка их кратности. В этой статье мы рассмотрим, как это можно сделать быстро и просто, используя Python.
Кратность числа – это возможность деления одного числа на другое без остатка. В Python есть несколько способов определить кратность числа, которые подходят для различных задач. Кроме того, в Python есть специальный оператор, который называется оператором модуля (%) и помогает узнать остаток от деления двух чисел.
Дальше мы рассмотрим несколько примеров использования Python для определения кратности числа. Кроме этого, мы изучим, как использование оператора модуля может помочь в проверке кратности. В результате этой статьи вы узнаете, как просто и быстро проверить кратность числа в Python и сможете применить полученные знания в своих проектах.
Что такое кратность числа
Кратность числа – это условие, при котором одно число делится на другое без остатка, то есть это значит, что число можно получить умножением какого-то числа на другое.
Например, число 6 кратно числу 3, потому что оно делится на 3 без остатка, то есть 6 = 3 × 2.
Часто кратность используется в различных математических вычислениях и алгоритмах, например, в поиске простых чисел или в разложении сложных чисел на множители.
Читать далее«Знак больше и меньше в математике: картинки и уроки для понимания направления» — Научитесь правильно использовать знаки больше и меньше в математике с помощью понятных картинок и подробных уроков. Узнайте, в какую сторону обращается каждый из этих знаков и как это влияет на решение уравнений и неравенств.
Кроме того, кратность может быть полезна в различных практических задачах, например, при расчете циклов оплаты или при выборе наиболее эффективных вариантов упаковки или расстановки предметов.
В программировании кратность может соответствовать требованию некоторых функций, что позволяет данную функцию выполнять только при условии, что аргумент, переданный в нее, является кратным некоторому числу.
Как найти кратность числа
Кратность числа — это количество раз, на которое данное число содержит в себе другое число (делитель) без остатка. Например, число 12 кратно 3, так как 3 может быть разделен на 12 без остатка 4 раза.
Существуют различные способы найти кратность числа:
- Проверка по определению: делаем проверку всех возможных делителей числа и считаем количество делителей, на которые число делится без остатка.
- Проверка с помощью модуля: в Python можно использовать оператор % (модуль), который показывает остаток от деления двух чисел. Если остаток равен 0, то число является кратным данному делителю.
- Проверка на «кратность числа n делителем m»: в этом случае нужно проверить, насколько n делится на целое число m и если имеется остаток при делении, то n не является кратным m.
Выбор метода зависит от задачи и типа чисел, с которыми вы работаете. Если вы хотите проверить множество чисел на кратность конкретному делителю, то использование оператора % будет более эффективным. Если вам нужно найти все делители числа, то проверка по определению будет более эффективным методом.
Метод деления с остатком
Метод деления с остатком является одним из базовых методов математики. Для проверки кратности числа нужно разделить это число на другое число (делитель) и посмотреть, получится ли одинаковый остаток при делении каждого из этих чисел на делитель.
Так, например, для того, чтобы проверить, кратно ли число 12 числу 4, нужно разделить 12 на 4 (12/4=3) и проверить, равен ли остаток от деления какого-либо числа на 4 нулю (например, 8/4=2, остаток 0, значит, число 8 кратно 4).
Метод деления с остатком используется в программировании для проверки кратности чисел. В Python для этого можно использовать оператор % (остаток от деления). Например, чтобы проверить, кратно ли число x числу y, нужно написать:
Читать далее«Как центрировать заголовок на сайте: правила установки в HTML» — в формате Как центрировать заголовок на сайте: правила установки в HTML.
if x % y == 0:
Оператор % возвращает остаток от деления, т.е. если x кратно y, то результат будет равен 0, иначе — ненулевое число.
Таким образом, метод деления с остатком является простым и эффективным способом проверки кратности чисел в Python.
Метод умножения на целое число
Метод умножения на целое число — один из простых способов определить является ли число кратным другому. Он основан на том, что если произведение двух чисел является целым числом, то одно из этих чисел является делителем другого. Таким образом, если мы умножим число на другое целое число, и результат будет целым числом, то мы можем заключить, что оно является кратным этому целому числу.
- Для того чтобы проверить, является ли число 15 кратным 3, мы можем умножить 3 на 5. Результатом будет число 15. Значит, 15 кратно 3.
- Для проверки, является ли число 28 кратным 4, мы можем умножить 4 на 7. Результатом будет число 28. Значит, 28 кратно 4.
Этот метод может использоваться для определения кратности чисел в программировании. В языке Python, чтобы проверить является ли число кратным другому, мы можем использовать оператор деления с остатком % и проверить, равен ли остаток от деления нулю. Например, для проверки, является ли число x кратным y, мы можем написать:
Таким образом, метод умножения на целое число является простым и эффективным способом определения кратности чисел.
Как проверить кратность числа в Python
Кратность числа — это свойство, описывающее, сколько раз одно число содержится в другом без остатка. В Python есть несколько простых способов проверить кратность числа.
Оператор % — используется для нахождения остатка от деления. Если остаток равен 0, значит число кратно. Например, чтобы проверить, что число 10 кратно 5, нужно написать:
Функция divmod — возвращает частное и остаток от деления в виде кортежа (tuple). Если остаток равен 0, то число кратно. Например:
Функция math.fmod — возвращает остаток от деления c плавающей точкой, что позволяет работать с большими числами. Если остаток равен 0, то число кратно. Например:
На практике чаще всего используется оператор %, так как он быстрее и работает со всеми типами данных. Однако в случае больших чисел, где точность имеет значение, лучше использовать math.fmod.
Оператор деления по модулю
Оператор деления по модулю (%), также известный как оператор остатка от деления, возвращает остаток от деления одного числа на другое.
Этот оператор может быть очень удобен при проверке кратности числа. Для этого нужно поделить число на другое число (например, 2 или 5) и проверить, равен ли остаток от деления нулю. Если да, то число кратно этому числу.
Кроме того, оператор деления по модулю может быть полезен при обращении к элементам списка или массива с помощью индексов. Если вы хотите получить элемент с индексом, который равен остатку от деления длины списка на какое-либо число, вы можете использовать этот оператор.
- 12 % 5 = 2 (12 делится на 5 два раза с остатком 2)
- 20 % 4 = 0 (20 делится на 4 пять раз без остатка)
- len(my_list) % 3 — получить элемент с индексом, который равен остатку от деления длины списка на 3
Использование оператора деления по модулю может упростить ваш код и сделать его более читаемым и понятным.
Операторы сравнения
В языке Python операторы сравнения используются для сравнения значений и возвращения истины или лжи в результате сравнения. Операторы сравнения позволяют сравнивать числа, строки, списки и другие типы данных.
Среди операторов сравнения в Python есть:
- == – равно – проверка на равенство двух значений;
- != – не равно – проверка на неравенство двух значений;
- – меньше – проверка на то, что первое значение меньше второго;
- > – больше – проверка на то, что первое значение больше второго;
- – меньше или равно – проверка на то, что первое значение меньше или равно второму;
- >= – больше или равно – проверка на то, что первое значение больше или равно второму.
Вот примеры использования операторов сравнения:
| == | 5 == 5 | Проверка на равенство | True |
| != | 5 != 5 | Проверка на неравенство | False |
| 3 < 5 | Проверка на меньше | True | |
| > | 3 > 5 | Проверка на больше | False |
| 3 | Проверка на меньше или равно | True | |
| >= | 3 >= 5 | Проверка на больше или равно | False |
Операторы сравнения можно использовать вместе с условными операторами, чтобы например проверять значения переменных и выводить различные сообщения, в зависимости от результата сравнения.
Как проверить кратность числа в одну строку
Проверка кратности числа — необходимый инструмент в различных задачах. Нередко процедура проверки может занимать несколько строк кода, что не всегда удобно. В Python есть способ проверки кратности числа в одну строку.
Для этого используется оператор «%» (процент), который возвращает остаток от деления. Если остаток отделения равен нулю, значит, число кратно другому числу.
Например, для того, чтобы проверить число «x» на кратность «y», достаточно написать следующее:
Таким образом, используя оператор «%» и условный оператор «if» можно проверять кратность чисел в одну строку.
Практические примеры
Если вам нужно проверить, является ли число кратным 2, проще всего проверить его остаток от деления на 2. Если остаток равен нулю, то число кратно 2. Пример использования:
Для проверки кратности числа 3 можно использовать то же самое правило. Если остаток от деления на 3 равен нулю, то число кратно 3. Пример использования:
Если вам нужно проверить кратность числа n, можно использовать такой же подход, проверяя остаток от деления на n. Пример использования:
Для проверки кратности нескольких чисел можно использовать цикл и список:
Если вы хотите найти все числа от 1 до n, кратные определенному числу, можно использовать цикл и список:
В таблице ниже приведены некоторые примеры использования описанных выше методов для проверки кратности чисел:
ЧислоКратность 2Кратность 3Кратность 5Числа, кратные 3 до 20
| 2 | Да | Нет | Нет | 3, 6, 9, 12, 15, 18 |
| 7 | Нет | Нет | Нет | 3, 6, 9, 12, 15, 18 |
| 10 | Да | Нет | Да | 3, 6, 9, 12, 15, 18 |
| 15 | Да | Да | Нет | 3, 6, 9, 12, 15, 18 |
Видео по теме:
Вопрос-ответ:
На чём основано определение кратности числа в Python?
Определение кратности числа в Python основано на делении числа на другое число и проверке остатка от этого деления.
Как можно проверить кратность числа 7 в Python?
Чтобы проверить, является ли число кратным 7 в Python, можно воспользоваться операцией деления с остатком и проверить, равен ли остаток от деления на 7 нулю. Например, так: if number % 7 == 0:
Можно ли проверить кратность числа сразу для нескольких чисел?
Да, можно. Для этого нужно использовать цикл, который будет проходить по всем числам и проверять их кратность. Например, так: for number in numbers: и затем в цикле выполнять проверку кратности.
Какая функция в Python позволяет проверить кратность числа?
В Python не существует встроенной функции для проверки кратности числа. Однако, для этой задачи можно написать свою функцию, используя операцию деления с остатком и условный оператор if.
Могут ли отрицательные числа быть кратными?
Да, отрицательные числа тоже могут быть кратными. Например, -14 кратно 7, потому что -14 = 7 * (-2).
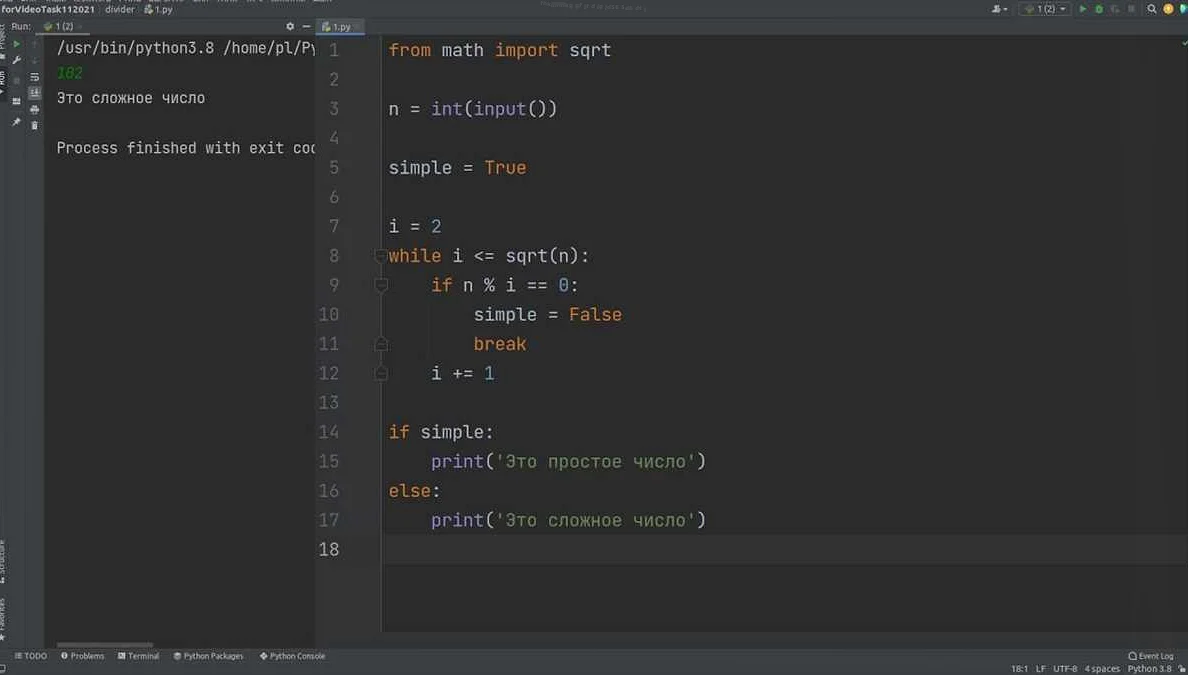
Как можно определить все делители числа в Python?
Чтобы определить все делители числа в Python, можно написать функцию, которая будет проверять кратность всех чисел от 1 до самого числа. Например, так:
def find_divisors(n):
divisors = []
for i in range(1, n + 1):
if n % i == 0:
divisors.append(i)
return divisors
Можно ли использовать оператор деления для проверки кратности числа?
Можно, но оператор деления в Python не всегда работает корректно для этой задачи, особенно если используются числа с плавающей точкой. Поэтому для проверки кратности лучше использовать операцию деления с остатком (оператор %).