Заполнение двумерного массива python numpy

Массив Numpy

Первое знакомство с библиотекой NumPy (Numerical Python) состоялось на двенадцатом занятии вводного курса. Затем мы несколько раз использовали эту библиотеку при построении моделей. Пришло время посвятить ее функционалу отдельный раздел.

Библиотека Numpy является основой для многих других библиотек в Питоне, например, Pandas, Matplotlib, scikit-learn или scikit-image. Главный объект библиотеки — массив Numpy (Numpy array). О нем мы поговорим сегодня.

На следующем занятии мы изучим математические операции над массивами, а через одно — рассмотрим работу со случайными числами.

• Понятие массива Numpy
• Как создать массив Numpy
  • Функция np.array()
  • Функция np.arange()
  • Тип данных элементов массива
  • Массив с нулевой размерностью
  • Одномерный массив (вектор)
  • Двумерный массив (матрица)
  • Трехмерный массив
  • Массив из нулей
  • Массив из единиц
  • Массив, заполненный заданным значением
  • Пустой массив Numpy
  • Функция np.linspace()
  • Функции np.random.rand() и np.random.randint()
  • Создание массива из функции
  • Матрица csr и метод .toarray()
  • Индекс элемента массива
  • Срез массива
  • Массив 2D
  • Массив 3D
  • Функция len()
  • Вхождение элемента в массив
  • Распаковка массива
  • Изменение элементов массива
  • Сортировка массива и обратный порядок его элементов
  • Изменение размерности
  • Объединение массивов
  • Фильтр (маска) массива
  • Вопросы для закрепления

  Понятие массива Numpy

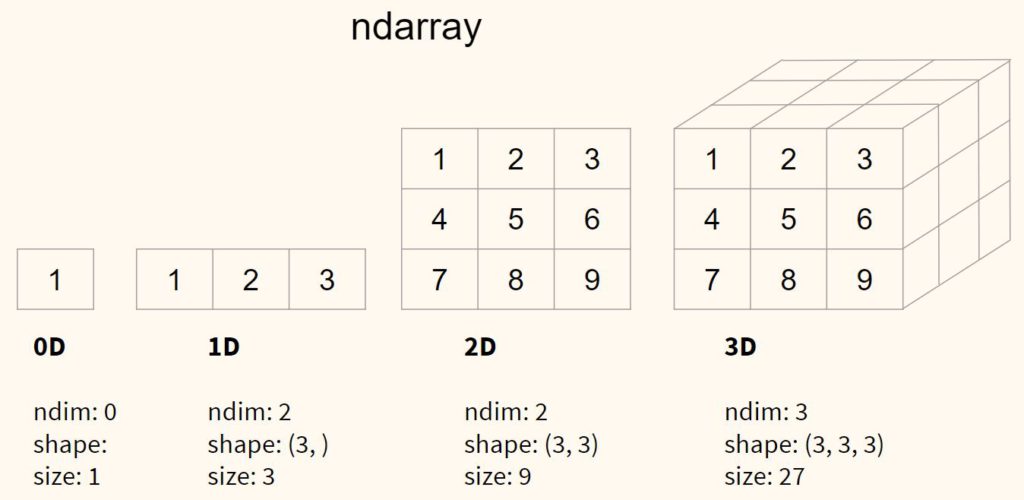
  Массив Numpy — это многомерный массив (ndarray, n-dimensional array) данных, над которыми можно быстро и эффективно выполнять множество математических, статистических, логических и других операций.

  Приведу пример массива с нулевым измерением, а также одно-, двух- и трехмерного массивов.

  

  Теперь посмотрим как работать с этими массивами на практике.

  Вначале нужно импортировать библиотеку Numpy.

  Как создать массив Numpy

  Рассмотрим два варианта создания одномерного массива.

  Функция np.array()

  Во-первых, массив можно создать с помощью функции np.array(), которой мы передаем, например, список или кортеж элементов.

  Функция np.arange()

  Кроме того, можно воспользоваться функцией np.arange(). Эта функция, как и функция range(), с которой мы уже знакомы, создает последовательность элементов. Обязательным параметром является верхняя граница, которая не входит в последовательность.

  Нижняя граница и шаг обязательными не являются.

  Отличие range() от функции np.arange() заключается в том, что первая не допускает использования типа float.

  

  При этом в массиве Numpy тип float вполне может использоваться.

  Тип данных элементов массива

  Как вы уже вероятно обратили внимание, в массивах тип данных определяется автоматически. При этом при создании массива мы можем задать этот параметр принудительно.

  Обратите внимание, в отличие, например, от списков, чаще всего в массивах содержатся элементы только одного типа (в частности, int или float).

  Свойства (атрибуты) массива

  Возьмем массив, который мы создали выше.

  Важным свойством (или как правильнее говорить атрибутом) массива является количество его измерений, ndim. В данном случае это одномерный массив или вектор.

  Теперь, с помощью атрибута shape, посмотрим на количество элементов в каждом измерении.

  Обратите внимание, даже когда массив одномерный, результат атрибута shape выводится в виде кортежа (на это указывают круглые скобки и запятая после цифры четыре).

  Атрибут size показывает общее количество элементов во всех измерениях.

  Как уже было сказано выше, атрибут dtype показывает тип данных отдельного элемента.

  Атрибут itemsize позволяет узнать размер в байтах (один байт состоит из 8 бит) одного элемента. В нашем случае, элемент (число) состоит из 64 бит, что составляет восемь байтов.

  Общий размер массива в байтах (nbytes) позволяет понять, в частности, поместится ли массив в оперативную память компьютера.

  Тот же результат можно получить, умножив общее количество элементов на размер одного элемента в байтах.

  Измерения массива

  Как уже было сказано, ndarray (массив Numpy) — это многомерный массив. Давайте еще раз взглянем на массивы с различными измерениями, добавив только что изученные атрибуты этих массивов.

  

  Теперь подробнее поговорим про размерность. Измерения (dimensions) создаются за счёт вложения одного массива в другой с помощью квадратных скобок []. Начнем с массива с нулевой размерностью.

  Массив с нулевой размерностью

  Массив с нулевой размерностью — это число (скаляр) и квадратных скобок не имеет.

  Посмотрим на свойства этого массива.

  Атрибут shape показывает отсутствие размерности, а size указывает на один элемент в массиве.

  Одномерный массив (вектор)

  Вложив несколько массивов с нулевой размерностью в квадратные скобки, мы получим одномерный массив или вектор.

  Снова воспользуемся атрибутами массива.

  Двумерный массив (матрица)

  Поместив во вторые квадратные скобки, например, два одномерных массива, мы получим двумерный массив или матрицу.

  Атрибут size двумерного массива более интуитивно понятен. В данном случае два элемента одного измерения умножены на три элемента второго.

  Добавлю, что с точки зрения Numpy матрица с одной строкой или одним столбцом — это разные объекты. Начнем с матрицы, которая имеет три вектора по одному элементу.

  Теперь наоборот, создадим матрицу с одной строкой, в которой три элемента.

  Трехмерный массив

  Теперь создадим трехмерный массив, внутри которого будут два двумерных массива 2 х 3. Общее количество элементов будет равно двенадцати (2 х 2 х 3). Визуально это можно представить как стэк (наложение) двух матриц.

  

  При этом, вместо того чтобы вручную прописывать все 12 значений, мы последовательно воспользуемся функцией np.arange() и методом np.reshape().

  Функция np.arange(), как мы уже видели выше, создаст одномерный массив из 12 элементов, а метод np.reshape() распределит их по измерениям. Выведем атрибуты.

  Обратите внимание, атрибут shape сначала выводит размерность внешнего измерения, в нем две матрицы. Далее в каждую матрицу вложены два одномерных вектора. В каждом векторе по три элемента.

  Аналогичным образом создаются четырехмерные массивы, а также массивы с большим количеством измерений.

  Понятие тензора

  Добавлю, что в математике n-мерный массив называется тензором, а числа (скаляры), векторы и матрицы являются его частными случаями для нуля, одного и двух измерений соответственно.

  

  Другие способы создания массива

  Массив из нулей

  Иногда бывает полезно создать массив, все элементы которого равны нулю. Для этого используется функция np.zeros().

  Массив из единиц

  В тех случаях когда нужно создать массив, заполненный единицами, можно воспользоваться функцией np.ones().

  Массив, заполненный заданным значением

  Функция np.full() создает массив, заполненный заданным значением.

  Пустой массив Numpy

  В отличие от предыдущих инструментов, функция np.empty() возвращает массив заданной размерности, но без инициализации его значений. Другими словами, пустой массив.

  Кроме того, любой массив Numpy можно преобразовать в описанные выше массивы с помощью функций np.zeros_like(), np.ones_like(), np.full_like() и np.empty_like(). Приведу пример для np.zeros_like().

  Примеры работы с тремя оставшимися функциями можно посмотреть в ноутбуке⧉.

  Функция np.linspace()

  Функция np.linspace() позволяет указать диапазон начального и конечного значений, а также количество равноудаленных точек внутри этого диапазона (включая начальное и конечное значения).

  Обратите внимание, функция np.linspace() сама определяет, где расставить точки. Нам нужно лишь указать их количество. Этим она отличается от функции np.arange(), в которой мы указываем шаг в пределах заданного диапазона.

  Функцию np.linspace() удобно использовать для построения графиков функций.

  

  В качестве примера выведем первые 10 точек, созданные функцией np.linspace().

  Функции np.random.rand() и np.random.randint()

  Массивы можно также создавать с помощью функций, генерирующих псевдослучайные числа. В частности, функция np.random.rand() создает массив заданной размерности, заполненный числами от 0 до 1 (единица в диапазон не входит).

  Функция np.random.randint() формирует массив целых чисел в заданном диапазоне (верхняя граница не входит в диапазон) и с заданной размерностью.

  Более подробно с этими и другими похожими функциями мы познакомимся на одиннадцатом занятии.

  Создание массива из функции

  Помимо вышеупомянутых способов массив можно создавать с помощью собственных функций. Для того чтобы понять, как это работает, вначале давайте вспомним координаты массива Numpy.

  

  Функция np.fromfunction() берет координаты (i, j) каждой ячейки и передает их в собственную функцию. Посмотрим, как это работает на практике.

  Теперь применим эту функцию к каждой ячейке (координатам) массива с размерностью (3, 3).

  В np.fromfunction() можно передать и lambda-функцию.

  Матрица csr и метод .toarray()

  Кроме этого в случае если данные хранятся в формате csr (сжатое хранения строкой, compressed sparse row), то мы можем преобразовать их обратно в массив Numpy с помощью метода .toarray().

  A = np . array ( [ [ 2 , 0 , 0 , 1 , 0 , 0 , 0 ] , [ 0 , 0 , 3 , 0 , 0 , 2 , 0 ] , [ 0 , 0 , 0 , 1 , 0 , 0 , 0 ] ] )

  Долю нулевых значений несложно посчитать через функцию np.count_nonzero() и атрибут size.

  Преобразуем матрицу в формат csr.

  Вернем матрицу csr обратно в формат массива Numpy.

  Напомню, что с форматом csr мы впервые познакомились, когда изучали рекомендательные системы. Метод .toarray() мы активно применяли на занятии по обработке естественного языка.

  Индексы и срезы

  Индекс элемента массива

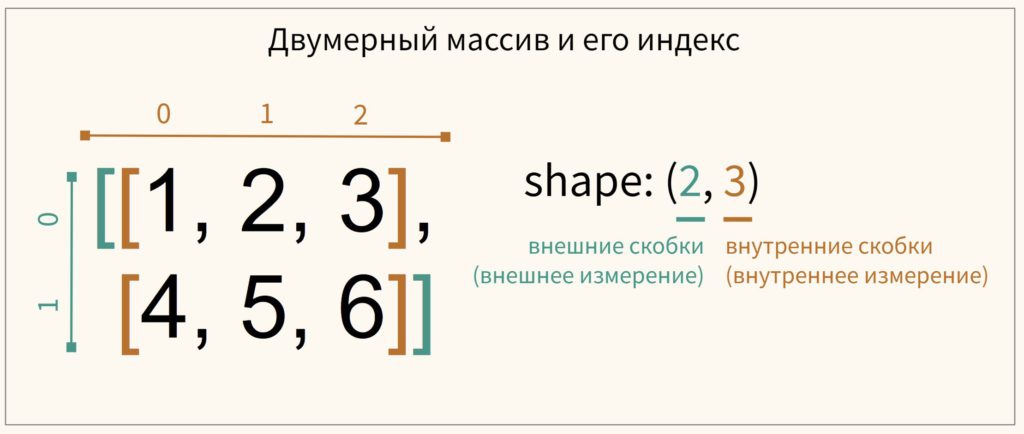
  Подобно спискам, к элементам массива можно получить доступ по их индексу. Главное отличие — необходимо учитывать наличие измерений. Вначале рассмотрим индексы массива на схеме.

  

  Если мы хотим получить доступ к элементу массива, то необходимо вначале указать индекс внешнего измерения (оно будет первым по счету в выводе атрибута shape), а затем индекс внутреннего.

  Другими словами, мы двигаемся как бы снаружи вовнутрь, перемещаясь из одного измерения в другое.

  Посмотрим, как это реализовать на Питоне. Создадим двумерный массив.

  Посмотрим на измерения и количество элементов в каждом из них.

  Выведем первый элемент первого (внешнего) измерения.

  Второй индекс позволяет обратиться, например, к первому элементу первого вектора.

  Теперь выведем значение шесть.

  Срез массива

  В массиве Numpy доступны и срезы (slice). Срез одномерного массива очень похож на срез списка.

  Возьмем каждый второй элемент в интервале с 1-го по 6-й индекс.

  

  Когда измерений больше одного, внутри квадратных скобок измерения отделяются запятой. Создадим двумерный массив.

  Сделаем срез из первой строки (внешнее измерение) и первых двух столбцов (внутреннее измерение).

  Если нужно взять все элементы одного из измерений, достаточно поставить двоеточие без указания индекса.

  С помощью среза можно вывести конкретный элемент массива.

  Другими словами, c [ 0 , 0 ] == c [ 0 ] [ 0 ] .

  Кроме того, обратите внимание, что индекс в формате array[i, j] и координаты элементов массива, которые мы рассмотрели ранее, это одно и то же.

  Допускаются срезы с отрицательным индексом.

  Рассмотрим более сложный пример. Возьмем всю вторую строку [ 1 ] и каждый второй столбец [ :: 2 ] .

  Теперь создадим массив с тремя измерениями.

  Можно сказать, что наш 3D массив состоит из четырех матриц 2 x 2.

  Вначале выведем значение десять. Если идти снаружи вовнутрь, получается, что это третья матрица [2], второй вектор [1] и первый элемент [0].

  Для срезов понадобится две запятых.

  Если указать только один срез, мы будем работать только во внешнем измерении (с четырьмя матрицами).

  Прежде чем завершить разговор про срезы, выведем первые строки каждой матрицы.

  Оси массива

  С концепцией измерения массива тесно связано понятие оси (axis, множественное число — axes). У массива столько же осей, сколько и измерений. Мы уже столкнулись с осями двух и трехмерного массивов, когда работали с изображениями.

  Рассмотрим этот вопрос ещё раз.

  Массив 2D

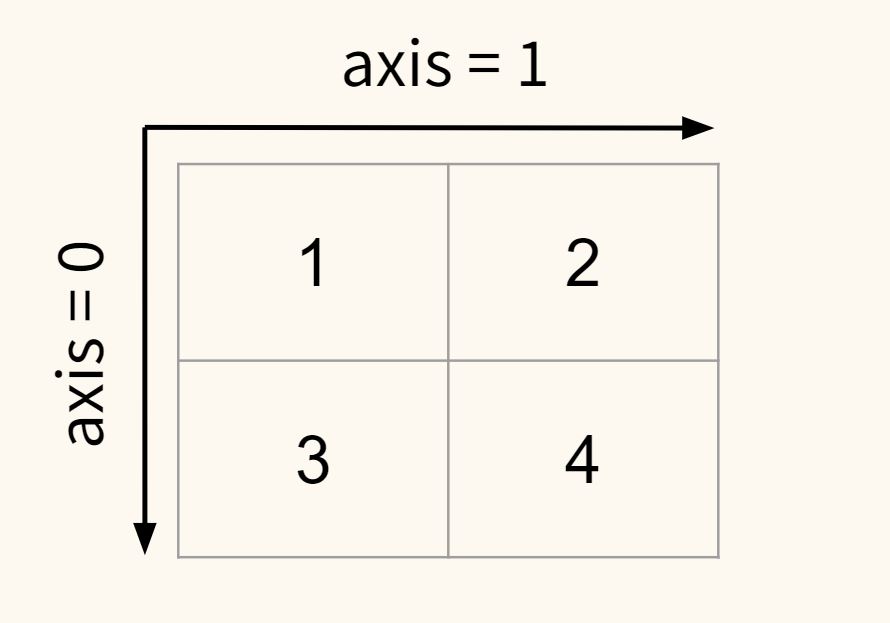
  В двумерном массиве два измерения и соответственно две оси.

  

  В документации Numpy существует такое понятие как первая и последняя ось. Применительно к двумерному массиву, ось 0 — это первая ось, а ось 1 — последняя.

  Многие, в частности, математические и статистические методы в Numpy предполагают указание параметра оси. Продолжим работу с приведенным выше двумерным массивом.

  Сложение вдоль первой оси (axis = 0)

  Найдем сумму по столбцам (вдоль оси 0).

  

  Сложение вдоль второй оси (axis = 1)

  Теперь найдем сумму по строкам (вдоль оси 1).

  

  Обратите внимание, хотя axis = 0 принято ассоциировать со строками двумерного массива, сложение происходит вдоль вертикальной оси или по столбцам. Параметр axis = 1, отвечающий за столбцы, наоборот предполагает сложение вдоль горизонтальной оси по строкам.

  При таких операциях говорят, что мы агрегируем (aggregate) данные и сворачиваем (collapse) или сокращаем (reduce) измерения вдоль определенной оси. И действительно, в каждой из описанных выше операций двумерный массив превратился в одномерный.

  Сложение вдоль обеих осей (axis = (0, 1))

  Если в параметр axis передать кортеж с указанием обеих осей (0, 1), сумма будет рассчитана сначала вдоль оси 0, затем вдоль оси 1.

  Источник

  Читайте также:  Get current line python