ЕГЭ по информатике 2023 — Задание 6 (Задачи с Черепахой)
Привет! Сегодня разберём новый тип 6 задания из ЕГЭ по информатике 2023! Добавим недостающий пазл в видеокурс по подготовке к ЕГЭ по информатике.
Так же Вы можете посмотреть разбор 6 задания из ДЕМОВЕРСИИ 2023.
На мой взгляд, на экзамене скорее всего будет задача, похожая именно на демонстрационный вариант. Т.к. это задание нового образца, то выпускникам необходимо привыкнуть к нему.
Вспомним, когда в прошлом году была введена новая формулировка для 3 задания, то на экзамене дали очень похожую задачу на ту, которая была в демоверсии.
Рассмотрим первую тренировочную задачу из 6 задания ЕГЭ по информатике 2023.
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 15 [Вперёд 15 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
В начале нужно понять, какая фигура получится в результате действий Исполнителя Черепахи.
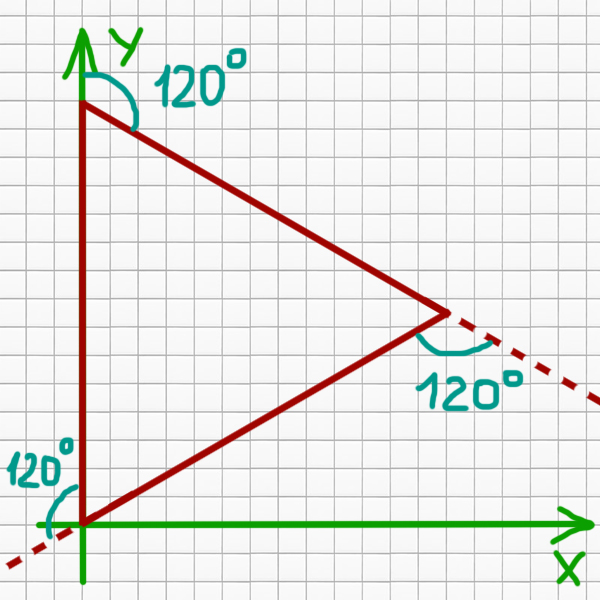
Черепаха идёт вверх на 15 единиц. Потом поворачивает направо на 120 градусов. Потом идёт на 15 единиц по заданному курсу и снова поворачивает на 120 градусов, идёт на 15 единиц ещё и попадает в исходную точку. В итоге получается равносторонний треугольник! Дальнейшие повторения не имеют смысла, т.к. нового больше ничего не нарисуется.
Проведём перпендикуляры от каждой точки с целыми координатами на оси Y внутри треугольника.
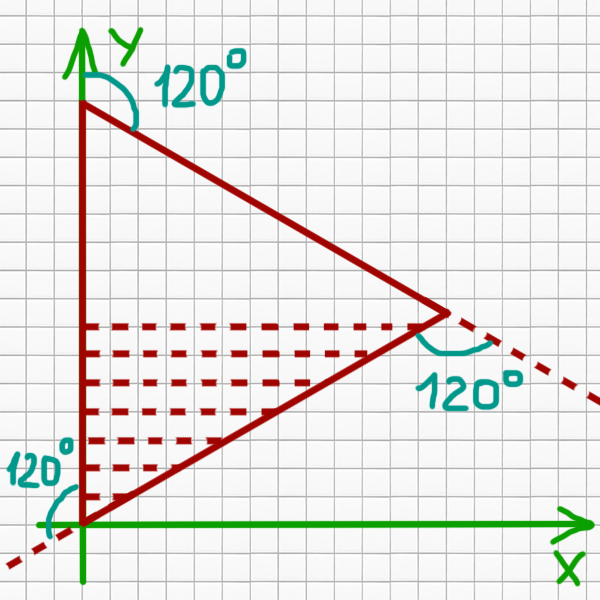
Для каждой точки на оси Y мы можем найти этот перпендикуляр. Это и есть искомое количество точек на каждой такой линии, если округлить это значение в меньшую сторону.
Посмотрим, как найти такой перпендикуляр, если точка на оси Y находится до середины стороны. Пусть есть точка (0, yn), а dn — это перпендикуляр для этой точки. Тогда
Для второй половины длины перпендикуляров будут такие же.
Напишем программу на Питоне, которая подсчитает все точки.
import math s=0 for y in range(0, 8): s = s + int(math.tan(math.pi / 3) * y ) s = 2*s print(s)
Нам необходимо взять первые 7 точек, дальше ситуация симметричная. Пишем в цикле for 8, потому что последнее число не проходится в Питоне.
Вычисляем по формуле длину каждого перпендикуляра. Тангенс вычисляется с помощью функции math.tan. Для неё нужна математическая библиотека math. Функция должна получить градусы в радианах, поэтому ей передаём π /3 = 60 o .
В цикле суммируем все точки для каждой линии. Результат нужно умножить на 2, чтобы учесть вторую половину треугольника.
Задача(Считаем точки вручную)
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Налево m (где m – целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 16 [Налево 36 Вперёд 4 Налево 36]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии следует учитывать.
В это задачке достаточно не просто составить уравнения прямых полученной фигуры. В таких случаях можно попробовать вручную посчитать точки с помощью известной программы Кумир от НИИСИ РАН. Скачать её можно с официального сайта НИИСИ РАН.
Вероятно, это программа окажется на компьютере на экзамене.
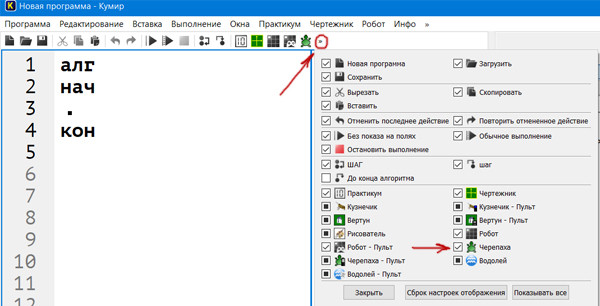
Запустим программу Кумир-Стандарт. В начале нужно подключить модуль Черепаха.
После того, как модуль Черепаха подключён, можно написать программу на языке Кумир.
использовать Черепаха алг нач опустить хвост нц 16 раз влево(36) вперед(4) влево(36) кц кон
В начале нужно подключить модуль Черепаха. Слово алг обозначает начало алгоритма. Слово нач — это начало программы.
Опускаем хвост у Черепахи. Цикл пишем с помощью команды нц — начало цикла. Команда кц — это конец цикла. Команда влево — это аналог команды Налево (видим, что эти команды пишутся по-разному). Аналогично есть команда вправо в программе Кумир. Команда вперед пишется без буквы ё.
После того, как алгоритм перенесли в программу Кумир, запускаем программу, нажав на кнопку F9 (или кнопка плей в виде треугольника).
После этого появится окно в правом нижнем углу. Это окно можно расширить до приемлемых размеров, чтобы нам было удобно анализировать рисунок.
Необходимо настроить масштабирование на 1.
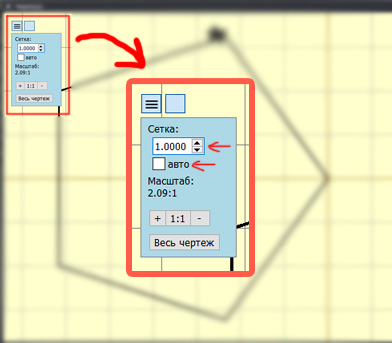
После этого можно сделать скриншот и перенести рисунок в программу Paint, где и посчитать точки вручную.
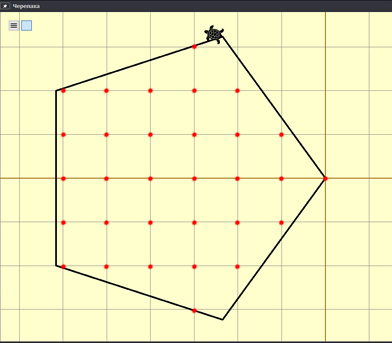
Получается в ответе 31 точка. Обратите внимание, что в этой задачи просили подсчитать точки, которые находятся на линиях в том числе.
Даже если нет программы Кумир, можно подсчитать точки вручную через Python. Напишем программу.
from turtle import * left(90) for i in range(16): left(36) forward(4*40) left(36) penup() for x in range(-10, 10): for y in range(-10, 10): setpos(x*40, y*40) dot(4, 'red')
Программа выведет такую картину.
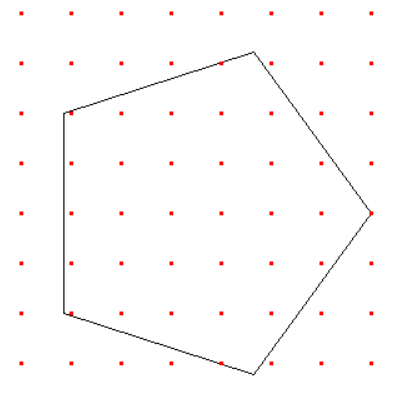
В программе подключаем модуль turtle. В начале повернём Черепаху на 90 градусов налево, с помощью команды left. Это делается из-за того, в Python Черепаха смотрит вдоль положительного направления оси абсцисс.
Далее идёт цикл, который указан в задаче. Он должен повторится 16 раз. Внутри цикла пишем программу для Черепахи. Команда left() — поворот налево (аналогично right() — поворот направо), команда forward() — это движение верёд.
4 единицы внутри команды forward() умножаются на 40. Число 40 — это коэффициент размера нашего рисунка. Попробуйте «поиграть» с этим числом, чтобы посмотреть эффект уменьшения или увеличения рисунка.
Команда penup() позволяет поднять кисть, чтобы проставить точки, которые будут символизировать точки с целыми координатами.
Далее идут вложенные циклы, с помощью них мы проставим точки с целыми координатами. Выбираем диапазон, чтобы наша фигура точно уместилась.
Команда setpos() ставим точки. Умножаем координаты x и y на тот же коэффициент, что использовали ранее.
Команда dot() устанавливает жирность и цвет точки.
Задача (Составляем уравнения)
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост поднят. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует три команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке; Опусти, принуждающая Черепаху опустить хвост.
Запись Повтори k [Команда 1 Команда 2 . Команда S] означает, что последовательность из S команд повторится k раз.
Черепахе был дан для исполнения следующий алгоритм:
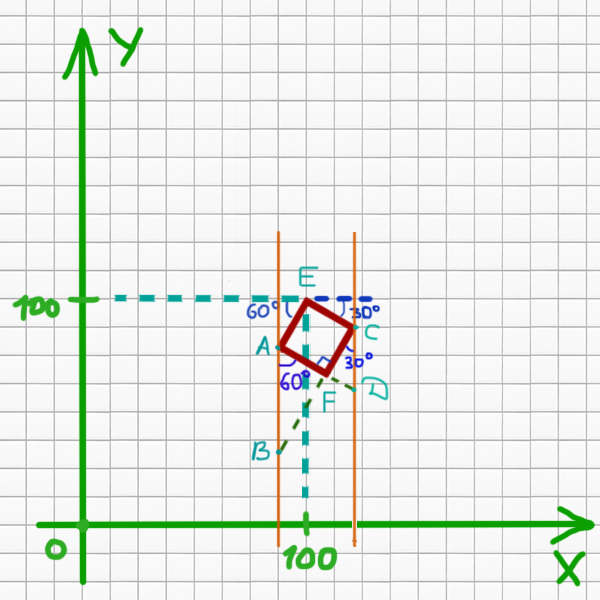
Вперёд 100 Направо 90 Вперёд 100 Направо 30 Опусти Повтори 10 [Вперёд 25 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
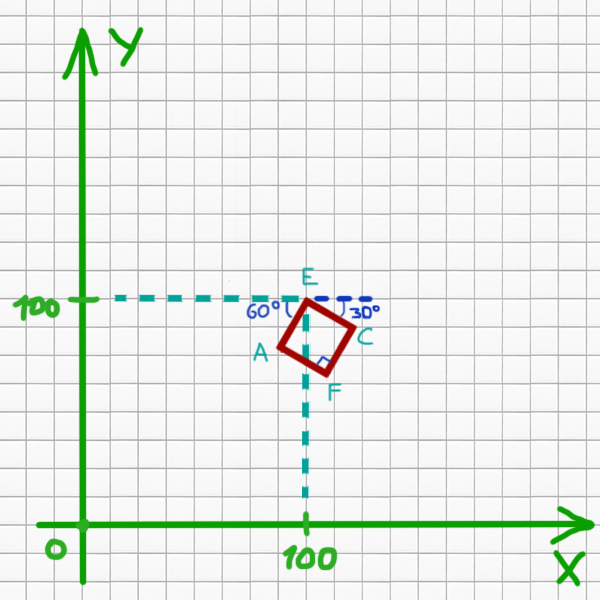
Здесь уже не очень удобно пользоваться элегантным способом. Составим уравнения прямых, которые образуют квадрат. Общий вид уравнения прямой выглядит так:
Коэффициент k — это тангенс угла наклона α к оси X ( 0 ≤ α π , но α ≠ π /2). Число b — это смещение прямой по оси Y относительно нуля.
Для прямой AE k1=tan(60 o )=√3. Так же она проходит через точку (100, 100).
Найдём число b. Подставим в общее уравнение координаты точки (100, 100):
y = k*x+b = √3*100 + b = 100
b=100*(1 — √3)
Получается уравнение прямой AE:
Найдём на сколько смещена FC по оси Y относительно AE.
cos(60 o ) = 25 (сторона квадрата) / AB
AB = 25 / cos(60 o ) = 25 / 0,5 = 50
Получается, что уравнение для прямой FC:
Для прямой EC k2=-tan(30 o ) = — √3/3. Эта прямая тоже проходит через точку (100, 100). Подставим эти координаты в уравнение и найдём b.
y = (-√3/3) * x + b = (-√3/3) * 100 + b = 100
b = 100(1 + √3/3)
Тогда уравнение для прямой EC получается:
Найдём на сколько смещена прямая AF относительно EC по оси Y.
cos(30 o ) = 25 (длина стороны) / CD
CD = 25 / cos(30 o ) = 25 / (√3/2) = 50/√3
Пробежимся с помощью Питона для переменной x от 0 до 150. Для переменной y от 0 до 100. Чтобы получить точку, используем вложенные циклы!
s=0 for x in range(1, 200): for y in range(1, 200): if (y < (3**0.5)*x + 100*(1-3**0.5)) and (y > (3**0.5)*x + 100*(1-3**0.5) - 50) and (y < (- 3**0.5 / 3)*x + 100*(1+ 3**0.5 / 3)) and (y > (-3**0.5/3)*x + 100*(1 + 3**0.5 /3) - 50 / 3**0.5 ): s=s+1 print(s)
Точки, которые лежат в квадрате должны удовлетворять следующим условиям:
Проверить выше или ниже некоторая точка M(xm, ym), чем прямая y=k*x+b, можно следующим образом:
Если ym > k*xm + b, то точка лежит выше прямой.
Если ym
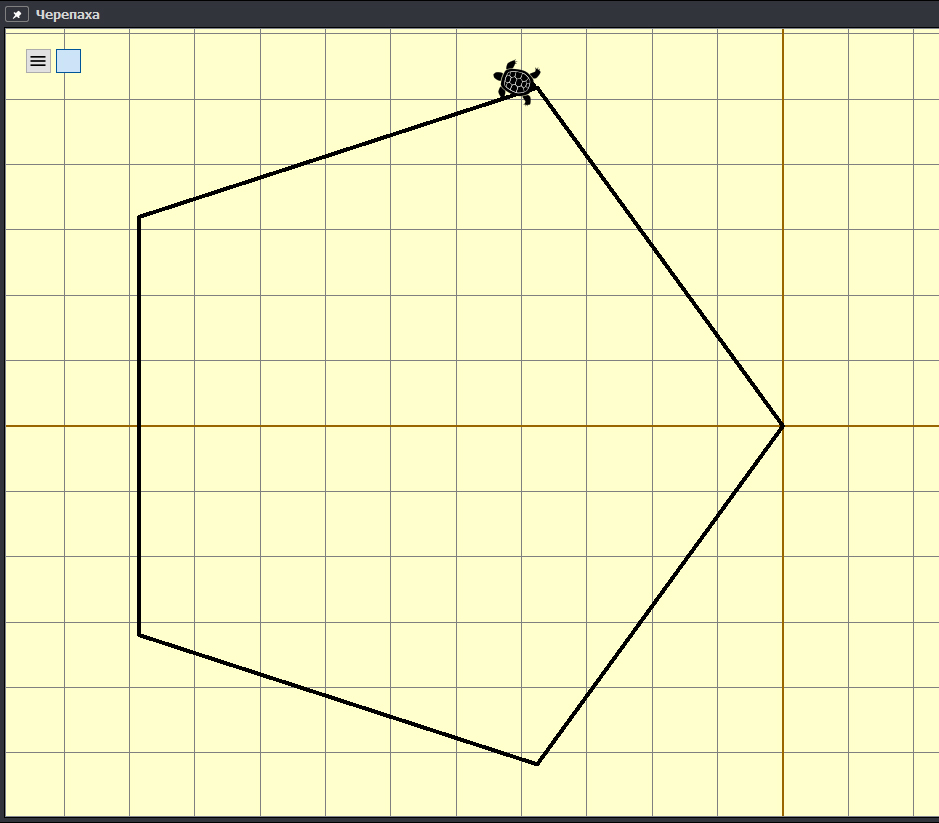
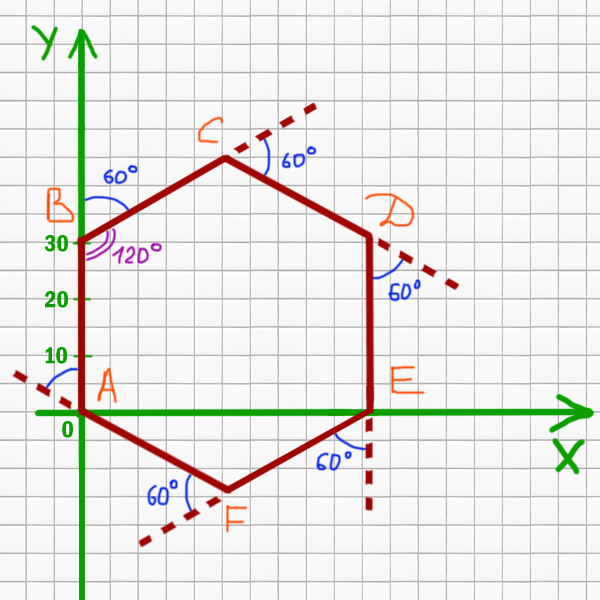
Получается правильный шестиугольник. Угол ∠СВА = 120 o . Как раз угол правильного n-угольника равен (n-2)*180 o /n. Для шестиугольника получается (6-2)*180 o /6 = 120 o .
Будем решать методом составления уравнений.
Рассмотрим прямую BC. Если провести от точки B прямую параллельную оси X, то мы увидим, что угол наклона прямой BC равен 30 o .
Прямая DC имеет угол наклона -30 o к оси X. Она расположена выше, чем BC на МВ. Треугольник BCM равносторонний. Значит, МВ=31. Тогда уравнение для DC будет:
Уравнение для AF будет:
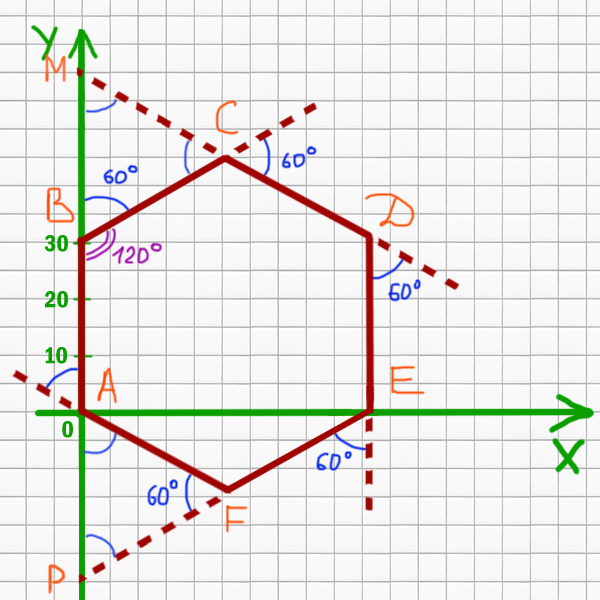
Прямая EF имеет угол наклона 30 o относительно оси X. Смещена она вниз на AP. Треугольник AFP так же является равносторонним. Следовательно, AP = 31. Тогда для EF получается:
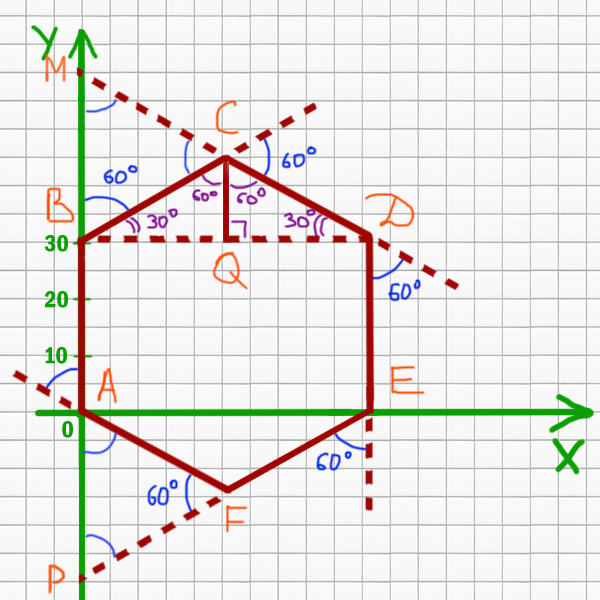
Прямая AB это x=0. Найдём так же ED.
cos(30 o ) = BQ / BC
BQ = BC * cos(30 o )
BQ = 31 * (√3/2)
BD = 2 * BQ = 2 * 31 * (√3/2) = 31 * √3
Значит, уравнение для ED: x = 31 * √3.
Когда уравнения готовы, можно написать программу.
k=0 for x in range(-100, 100): for y in range(-100, 100): if (y < 3**0.5 / 3 * x + 31) and (y < -(3**0.5) / 3 * x + 62) and (y > -(3**0.5) / 3 * x) and (y > 3**0.5 / 3 * x - 31) and (x > 0) and (x < 31 * 3**0.5): k=k+1 print(k)
Точки должны быть ниже прямых BC и CD, но выше прямых AF и EF. Так же координаты x должны быть 0