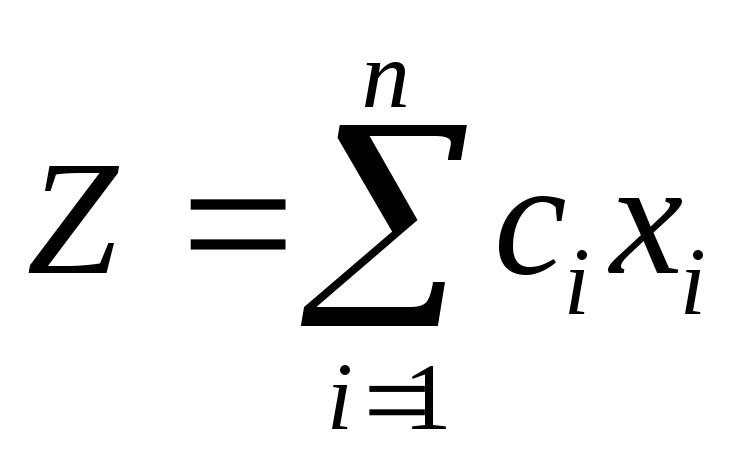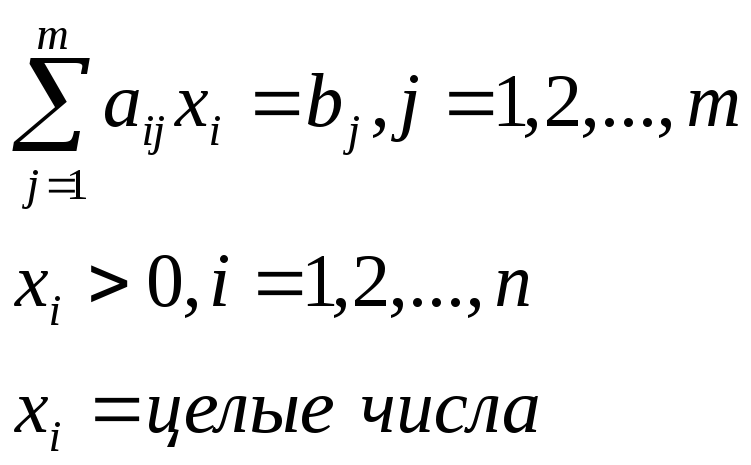Задачи целочисленного программирования графический метод решения задач

Графический метод решения ЗЛП

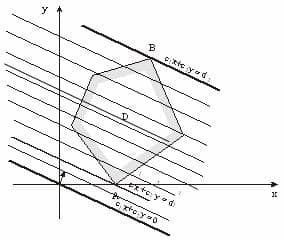
В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений (см. рисунок).

Инструкция . Выберите количество строк (количество ограничений). Если количество переменных больше двух, необходимо систему привести к СЗЛП (см. пример и пример №2). Если ограничение двойное, например, 1 ≤ x₁ ≤ 4 , то оно разбивается на два: x₁ ≥ 1 , x₁ ≤ 4 (т.е. количество строк увеличивается на 1).
Построить область допустимого решения (ОДР) можно также с помощью этого сервиса.

Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.

1. На плоскости X₁0X₂ строят прямые.
2. Определяются полуплоскости.
3. Определяют многоугольник решений;
4. Строят вектор N(c₁,c₂), который указывает направление целевой функции;
5. Передвигают прямую целевую функцию c₁x₂ + c₂x₂ = 0 в направлении вектора N до крайней точки многоугольника решений.
6. Вычисляют координаты точки и значение целевой функции в этой точке.

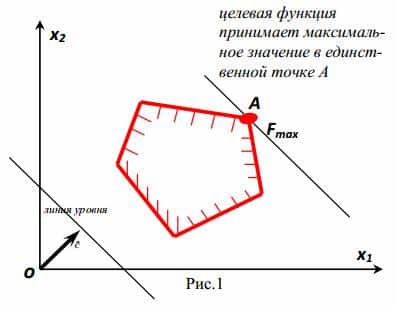
Целевая функция принимает экстремальное (минимальное или максимальное) значение в единственной точке А.

1. Сформулировать математическую модель задачи линейного программирования.
2. Решить задачу линейного программирования графическим способом (для двух переменных).

Если количество переменных в задаче линейного программирования больше двух, то задачу предварительно сводят к стандартной ЗЛП.
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅ → max при ограничениях:
x₁ + x₂ + x₃=12
2x₁ — x₂ + x₄=8
— 2x₁ + 2x₂ + x₅=10
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:

1	1	1	0	0	12
2	-1	0	1	0	8
-2	2	0	0	1	10

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₃.
2. В качестве базовой переменной можно выбрать x₄.
3. В качестве базовой переменной можно выбрать x₅.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x₁ + x₂ + x₃ = 12
2x₁ — x₂ + x₄ = 8
— 2x₁ + 2x₂ + x₅ = 10
Выразим базисные переменные через остальные:
x₃ = — x₁ — x₂+12
x₄ = — 2x₁ + x₂+8
x₅ = 2x₁ — 2x₂+10
Подставим их в целевую функцию:
F(X) = 3x₁ — 2x₂ + 5(- x₁ — x₂+12) — 4(2x₁ — 2x₂+10)
или
F(X) = — 10x₁ + x₂+20 → max
Система неравенств:
— x₁ — x₂+12 ≥ 0
— 2x₁ + x₂+8 ≥ 0
2x₁ — 2x₂+10 ≥ 0
Приводим систему неравенств к следующему виду:
x₁ + x₂ ≤ 12
2x₁ — x₂ ≤ 8
— 2x₁ + 2x₂ ≤ 10
F(X) = — 10x₁ + x₂+20 → max

Особенности решения задач линейного программирования графическим методом

Переменную x₂ принимаем в качестве дополнительной переменной и делаем замену на знак «≥»:
f=x₁ + 6x₃+ 27
x₁ + 3x₃≥6

Далее задача решается графическом способом.

Пример №2
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅ → max при ограничениях:
x₁ + x₂ + x₃=12
2x₁ — x₂ + x₄=8
— 2x₁ + 2x₂ + x₅=10
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:

1	1	1	0	0	12
2	-1	0	1	0	8
-2	2	0	0	1	10

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₃.
2. В качестве базовой переменной можно выбрать x₄.
3. В качестве базовой переменной можно выбрать x₅.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x₁ + x₂ + x₃ = 12
2x₁ — x₂ + x₄ = 8
— 2x₁ + 2x₂ + x₅ = 10
Выразим базисные переменные через остальные:
x₃ = — x₁ — x₂+12
x₄ = — 2x₁ + x₂+8
x₅ = 2x₁ — 2x₂+10
Подставим их в целевую функцию:
F(X) = 3x₁ — 2x₂ + 5(- x₁ — x₂+12) — 4(2x₁ — 2x₂+10)
или
F(X) = — 10x₁ + x₂+20 → max
Система неравенств:
— x₁ — x₂+12 ≥ 0
— 2x₁ + x₂+8 ≥ 0
2x₁ — 2x₂+10 ≥ 0
Приводим систему неравенств к следующему виду:
x₁ + x₂ ≤ 12
2x₁ — x₂ ≤ 8
— 2x₁ + 2x₂ ≤ 10
F(X) = — 10x₁ + x₂+20 → max

• Составить систему математических зависимостей (неравенств) и целевую функцию.
• Изобразить геометрическую интерпретацию задачи.
• Найти оптимальное решение.
• Провести аналитическую проверку.
• Определить существенные и несущественные ресурсы и их избытки.
• Определить значение целевой функции.
• Вычислить объективно обусловленные оценки.
• Составить соотношение устойчивости.

Источник

Глава 4 . Целочисленное программирование

§ 1 Постановка задачи целочисленного программирования.

В ряде экономических задач, относящихся к задачам линейного программирования, элементы решения должны выражаться в целых числах. В этих задачах переменные означают количество единиц неделимой продукции.

Задача целочисленного программирования формулируется следующим образом:

Найти такое решение план Х=(х₁, х₂,…, х_n), при котором линейная функция принимает максимальное или минимальное значение при ограничениях

задача решается методами линейного программирования. В случае если переменные оптимального решения оказываются нецелочисленными, то, применяя методы отсечения или метод перебора целочисленных решений.

Понятия о методе ветвей и границ.

Метод ветвей и границ заключается в упорядоченном переборе вариантов и рассмотрении лишь тех из них, которые оказываются по определенным признакам перспективными, и отбрасывании бесперспективных вариантов.

Метод ветвей и границ состоит в следующем: множество допустимых решений (планов) некоторым способом разбивается на подмножества, каждое из которых этим же способом снова разбивается на подмножества. Процесс продолжается до тех пор. Пока не получено оптимальное целочисленное решение исходной задачи.

Название метода ветвей и границ исходит из того, что в процессе решения задача последовательно «ветвится», заменяясь более простыми. Процесс решения можно продолжать в виде дерева, цифры в узлах (вершинах) которого обозначают план решения задачи (искомые переменные).

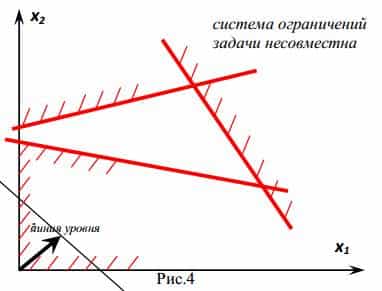
§ 2 Графический метод решения задач целочисленного программирования.

При наличии в задаче линейного программирования двух переменных, а в системе ограничения – неравенств, она может быть решена графическим методом без требований целочисленных переменных.

Если оптимальное решение этой задачи является целочисленным, то оно и является оптимальным для исходной задачи.

Если же полученное оптимальное решение не целочисленное, то строится дополнительное линейное ограничение. Оно обладает следующими свойствами:

1. Оно должно быть линейным;
2. Должно отсекать найденный оптимальный не целочисленный план;
3. Не должно отсекать ни одного целочисленного плана.

Алгоритм графического решения задачи целочисленного программирования.

1. Построить систему координат x₁0х₂ и выбрать масштаб.
2. Найти область допустимых решений (ОДР) системы ограничений задачи.
3. Построить целевую функцию, являющуюся линией уровня и на ней указать направление нормали.
4. Переместить линию целевой функции по направлению нормали через ОДР, чтобы она из секущей стала касательной к ОДР и проходила через наиболее удаленную от начала координат точку. Эта точка будет являться точкой экстремума, т.е. решением задачи.

1. Найти координаты, точки экстремума и значение целевой функции в ней. Если полученные значения не целочисленные, то перейти к следующему шагу.
2. Выделить у этих координат область с целочисленными значениями.
3. Определить новые координаты и построить граф.
4. Найти точки с целыми значениями искомых переменных, подставить в уравнение целевой функции и найти её значение. Максимальное из полученных значений целевой функции и будет решением задачи.

Источник

4.1. Постановка задачи. Графический метод решения

Двойственный симплекс-метод, как и обычный симплекс-метод, используется для решения задач линейного программирования. Но, в отличие от обычного симплекс-метода, его можно применять и в случае, если свободные члены системы нетривиальных ограничений являются отрицательными числами (при решении задачи симплексным методом эти числа предполагаются неотрицательными). Пусть требуется найти максимальное значение функции z = c 1 x 1 + c 2 x 2 + . + c n x n + c 0 при условиях

x 1 + a 1, m + 1 x m + 1 + . + a 1 n x n = b 1 ,
x		+ a	x	+ . + a		x = b ,
2	2, m + 1 m + 1		2 n n		2
.
x		+ a	x	+ . + a	x	= b ,
m	m , m + 1 m + 1			mn n	m
≥ 0,	j = 1. n .
				x j

Присоединим к системе ограничений целевую функцию z , исключив из нее базисные переменные и записав ее в виде уравнения z +∆ m + 1 x m + 1 + . +∆ n x n = ∆ 0 . Напомним, что, коэффициенты ∆ j , j = 1, , n называются оценками соответствующих переменных x j . Заметим, что среди чисел b i могут быть отрицательные. При этом, хотя точка X = ( b 1 , b 2 . b m ,0. 0) является решением системы нетривиальных ограничений, она не является планом исходной задачи, так как среди ее координат имеются отрицательные числа. Определение 4.1. Решение X = ( b 1 , b 2 . b m ,0. 0) системы не- тривиальных ограничений называется псевдопланом (псевдорешением) задачи линейного программирования, если ∆ j ≥ 0, j = 1, , n. Основными предпосылками для решения задачи линейного программирования двойственным симплекс-методом являются следующие две теоремы. Теорема 4.1. Если в псевдоплане X = ( b 1 , b 2 . b m ,0. 0) , есть хотя бы одно отрицательное число b i < 0 такое, что все a ij ≥ 0 при i = 1, , m , то задача не имеет решений. Теорема 4.2. Если в псевдоплане X = ( b 1 , b 2 . b m ,0. 0) , имеются отрицательные числа b i < 0 такие, что для любого из них существуют числа a ij < 0 , то можно перейти к новому псевдоплану, при ко- тором значение целевой функции задачи не уменьшится. Сформулированные теоремы дают основание для построения алгоритма двойственного симплекс-метода. Пусть X = ( b 1 , b 2 . b m ,0. 0) – псевдоплан исходной задачи. На основе условия задачи составляем симплекс-таблицу, в которой элементы свободного столбца могут быть отрицательными числами:

базис	b i	x 1	x 2	x l	x m		x m + 1	x n
x 1	b 1	1	0	0	0		a 1, m + 1	a 1 n
x 2	b 2	0	1	0	0		a 2, m + 1	a 2 n
.
x l	b l	0	0	1	0		a l , m + 1	a l , n
0
x m	b m	0	0	0	1		a m , m + 1	a mn
z	∆ 0	0	0	0 0	0 0		∆ m + 1	∆ n

1. Проверяем псевдоплан на оптимальность. Если b i ≥ 0 ( i = 1, , m ), то, так как, по предположению, все ∆ j ≥ 0 , псевдоплан X = ( b 1 , b 2 . b m ,0. 0) будет оптимальным решением исходной зада- чи. Если же в столбце свободных членов имеются отрицательные числа, то либо устанавливаем неразрешимость задачи (на основании теоремы 1), либо переходим к новому псевдоплану. 2. Выбираем разрешающую строку как содержащую наибольшее по абсолютной величине отрицательное число в столбце свободных членов (пусть это строка со свободным членом b l ). Для выбора раз- решающего столбца находим минимум модуля отношения элементов строки оценок к отрицательным элементам l -ой строки, т.е. находим min( −∆ j / a lj ), где a lj < 0 . Пусть это минимальное значение принима- ется при j = r , тогда в базис вводят переменную x r , а число a lr явля- ется разрешающим элементом. Переход к новой симплекс-таблице производят по обычным правилам симплексного метода. 3. Находим новый псевдоплан и переходим к пункту 1. Пример 4.2. Найти максимальное значение функции z = x 1 + x 2 + 2 x 3 при условиях x 1 + x 2 + x 3 = 8, x 1 − x 2 ≥ 4, x 1 + 2 x 2 ≥ 6, x 1 ≥ 0, x 2 ≥ 0, x 3 ≥ 0. Решение. Запишем исходную задачу линейного программирования в канонической форме, введя балансовые переменные x 4 , x 5 , а затем перепишем ее так, чтобы коэффициенты при базисных переменных были равны 1.

z = x 1 + x 2 + 2 x 3 → max
x	+ x	+ x		= 8,
1	2	3
x 1	− x 2	− x 4		= 4,		, то есть
x	+ 2 x		− x	= 6,
1	2	5
j = 1, ,5.
			x j ≥ 0,

Исключив из целевой функции x 3 , плекс-таблицу

z = x 1 + x 2 + 2 x 3 → max x 1 + x 2 + x 3 = 8, − x 1 + x 2 + x 4 = − 4, − x 1 − 2 x 2 + x 5 = − 6, x j ≥ 0, j = 1, ,5. получаем следующую сим-

Б.П.	с.ч. х 1		х 2 х 3 х 4 х 5
х 3	8	1	1	1	0	0
х 4	-4	-1	1	0	1	0
х 5	-6	-1 -2		0	0	1
z	16	1	1	0	0	0

Так как в столбце свободных членов имеются два отрицательных числа − 4 и − 6, а в последней строке нет отрицательных чисел, то в соответствии с алгоритмом двойственного симплекс-метода переходим к новой симплекс-таблице. Заметим, что в данном случае это можно сделать, так как в строках, содержащих отрицательные свободные члены ( − 4 и − 6) есть отрицательные числа. Так как наибольшее по модулю отрицательное число в столбце свободных членов есть − 6, то исключаем из базиса переменную x 5 . Чтобы определить раз-

решающий столбец, находим	1	1	1	, т.е. минимальное
	min −	, −	=
					− 1		− 2	2

отношение элементов строки оценок к отрицательным числам разре-

шающей строки (с противоположным знаком)						дает столбец x 2 . Ум-
ножаем третью строку		на	− 1/ 2	и переходим к			новой симплекс-
таблице
Б.П.	с.ч. х 1		х 2	х 3	х 4	х 5
х 3	5	1/2	0	1	0	1/2
х 4	-7	-3/2	0	0	1	1/2
х 2	3	1/2	1	0	0	-1/2
z	13	1/2	0	0	0	1/2

Аналогично, так как в свободном столбце последней таблицы есть отрицательное число − 7, то рассмотрим элементы второй строки. Среди этих чисел есть одно отрицательное − 3/ 2 . Если бы такое число отсутствовало, то исходная задача была бы неразрешима. Выбор раз-
решающего элемента здесь однозначен, умножаем вторую строку на − 2/3 и переходим к новой симплекс-таблице Б.П. с.ч. х 1 х 2 х 3 х 4 х 5

х 3	8/3	0	0	1	1/3	2/3
х 1	14/3	1	0	0	-2/3	-1/3
х 2	2/3	0	1	0	1/3	-1/3
z	32/3	0	0	0	1/3	2/3

Таким образом, в последней строке и в столбце свободных чле-

нов нет отрицательных элементов, поэтому план X	*	14	,	2	,	8	явля-
	=	3		3		3

ется оптимальным и z max = z ( X ) = 32 / 3. Задачи для самостоятельного решения Двойственным симплекс-методом найти решения следующих задач линейного программирования:

− 2 x −				2 x			+ x = − 1,
1	2	5
58.	z = − x 1 − 10 x 2	+ 10 → max при x ≥ 0 и − 2 x 1 + 2 x 2 + x 3 = − 2,
− 4 x +				2 x + x = − 1.
1	2	4
− 2 x + x					= − 1,
59.	z = − 2 x 2 − 4 x 4	1	2	= − 2,
		− 3 → max при x ≥ 0 и − x 2				+ x 3 − x 4
2 x		− 4 x		+ x			= − 1.
2		4		5
2 x			− 3 x		+ x			= − 11,
1	2	5
60.	z = − 5 x 2 − 4 x 3	+ 4 → max при x ≥ 0 и − 2 x 2 + 3 x 3 − x 5 = − 9,
− x			+ x	= − 2.
2	4
− 3 x − 4 x							= − 17,
61.	z = − 2 x 1 − 6 x 3	1	2
		+ 44 → max при x ≥ 0 и − 2 x 2 − 3 x 3 + 2 x 5 = − 9,
− x + 3 x						= − 1.
3	4
x	− x −			2 x		= − 7,
1		4	5
62.	z = − 5 x 4 − 7 x 5	− 7 → max при x ≥ 0 и − x 3 + 3 x 4 − 6 x 5 = − 3,
− x			− x	− 4 x				= − 11.
2	4		5

Источник