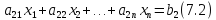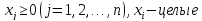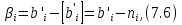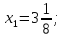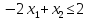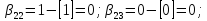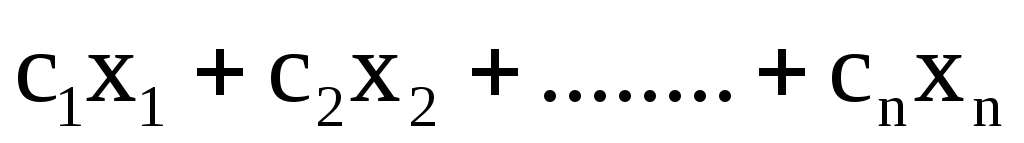Глава 3. Целочисленное линейное программирование.
Важное значение в ЛП имеет случай, когда неизвестные целочисленные.Задача ЛП с дополнительным условием целочисленности неизвестных исследуется в новойобласти математического программирования – целочисленном (дискретном) программировании (ЛЦП).
§1 Метод Гомори
К основной задаче ЛП добавим дополнительное условие – условие целочисленности неизвестных, в результате получим задачу ЛЦП. Можно, конечно, получить дробное оптимальное решение задачи ЛП и его округлить до ближайших целых значений. Но тогда может случиться, что мы будем либо близки к оптимальному плану задачи ЛЦП, либо далеки, либо вообще уйдем за пределы множества планов ЛЦП.Один из возможных методов решения задачи ЛЦП – метод Гомори.Идея метода базируется на представлении вещественного числа в виде суммы его целой и дробной частей.Как известно, целой частью вещественного числа «а» называется наибольшее целое число, не превосходящее
Обозначение целой части[a].Разность
есть дробная часть числа
Очевидно, например, что
и
Например:
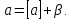
Рассмотрим метод Гомори на примере (общая задача ЛП):
План задачи линейного программирования называют целочисленным, если все его составляющие целые числа.
Для определения целочисленного решения задачи:
можно использовать алгоритм Гомори, состоящий из следующих этапов.
Первый этап. Задача (7.1) — (7.3) решается симплекс-методом до получения оптимального плана.
Второй этап.В последнюю симплекс-таблицу, содержащую оптимальный план, добавляют ограничение
составленное для i- ой строки следующим образом:
(Символом [a] обозначают целую часть числаa, то есть наибольшее целое число, не превосходящееa).
Третий этап.В последней симплекс-таблицевыбирают введенную строку разрешающей.Разрешающий столбец выбирают по правилу двойственного симплекс-метода. С выбранным таким образом разрешающим элементом осуществляют переход по известному алгоритму к следующей симплекс-таблице. Если при этом полученное решение окажется еще не целочисленным, то общий шаг повторяют.
1. Признаком отсутствия целочисленного решения в задаче (7.1)-(7.4) служит появление хотя бы одной строки с дробным свободным членом и целыми остальными коэффициентами. То есть в этом случае соответствующее уравнение не имеет решения в целых числах.
2. Дополнительное ограничение целесообразно составлять для строки, содержащей в столбце свободных членов наибольшую дробную часть.
3. Дополнительное ограничение можно составлять несколько иначе, то есть в качестве коэффициентов при неизвестных выбрать единицы. Тем самым получим ограничение в виде
.
Схема решения задачи (7.1) – (7.4)
- Исходную задачу решают симплекс-методом до получения оптимального решения без учета требования целочисленности его.
- Составляют дополнительное ограничение для строки, содержащую наибольшую дробную часть в столбце свободных членов.
- Коэффициенты нового ограничения вносят в последнюю симплекс-таблицу.
- Введенную строку выбирают разрешающей.
- Разрешающий элемент выбирают по принципу двойственного симплекс-метода.
- С выбранным таким образом разрешающим элементом осуществляют переход (по известным правилам) к следующей симплекс-таблице.
- В случае необходимости составляют еще одно дополнительное ограничение и процесс повторяют до получения целочисленного решения.
Пример.
(1) Отбросим пока условие целочисленности (*) и решим задачу ЛП
(2) Задача ЛП – каноническая. Исходная таблица
| B | Свободный член | Коэффициенты при неизвестных | |||
 |  |  |  | ||
 | 15 |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
Итерация 1
| B | Свободный член | Коэффициенты при неизвестных | |||
 |  |  |  | ||
 |  |  |  |  | |
 |  |  |  |  | |
 |  |  |  | ||
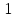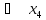Итерация 2
| B | Свободный член | Коэффициенты при неизвестных | |||
 |  |  |  | ||
 |  |  |  |  | |
 |  |  |  |  | |
 |  |  |  | ||
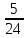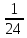План: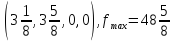 
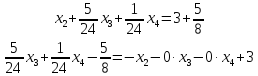
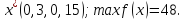
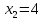
оказался нецелочисленным.Для отыскания целочисленного плана применим метод Гомори (метод отсечений). С этой целью из завершающей симплексной таблицы выпишем каноническую систему (3) (эквивалентная системе (2)): 
(3) Свободные члены обоих уравнений дробные. Выбираем первое уравнение (с наибольшим дробным свободным членом):
Рассмотрим неравенство (т. н. неравенство Гомори) 
(3)* Запишем (с положительным свободным членом) 
. (3)** В [4, с. 173] показано, что любой целочисленный план задачи (2) удовлетворяет и неравенству (3)*. Оптимальный же (нецелочисленный) план задачи (2) не удовлетворяет неравенству (3)*. Добавим неравенство (3)** к условиям задачи (2), то есть: 
, а т.к. системы были эквивалентны, то задача ЛЦП запишется ((3) +(3)** ):
(4) Задача (4) почти каноническая (
=1,2,3….). Решая задачу, получим оптимальный план 
Замечание 1. Ясно, что всякое дополнительное ограничение сужает область допустимых значений и максимум может быть только меньше или равен, но никак не больше. Оптимальный нецелочисленный план при этом отсекается. Если бы при решении задачи (4) план получился бы нецелочисленным, то необходимо вновь выписать неравенство Гомори к канонической системе из последней симплексной таблицы (новой) и далее вновь решать задачу ЛП и т.д., пока план оптимальной не окажется целочисленным. Замечание 2. Если левая часть уравнения системы имеет дробные часть равные 0, а правая часть дробная, то задача ЛЦП планов не имеет, например
. Здесь при целых значениях неизвестных никак не получится дробь 
, т.е. неизвестные нецелочисленны, поэтому для составления неравенства Гомори берем уравнения с дробной левой частью.Замечание 3. Ранее, когда решали задачу ЛП оптимальный план был: 
. Сейчас получили 
. Если бы не применили для решения задачи ЛЦП метод Гомори, а просто округлили бы, глядя на решение задачи ЛП, например, 
,
; или
или
,
то эти планы вообще выходят за пределы множества планов, т.к. не удовлетворяют системе задачи (1), в частности, системе 
Ну, а если округлить 
,
, то хотя это и план, ноf(x) = 39, а у нас
, т.е. значенияf(x) значительно отличаются. Пример.Найти 
при условиях: 
Снимем условие целочисленности. MaxZ=x1 + 2×2 при условиях: x1— 2x2+x3 = 2 — 2x1+x2+x4=2 x1+x2+x5=3 
. Исходная симплексная таблица
Базисные переменные  | Свободные члены ( ) | Коэффициенты при неизвестных | ||||
 |  |  |  |  | ||
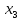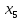 | 2 | 1 | -2 | 1 | ||
 | 2 | -2 | 1 | 1 | ||
 | 3 | 1 | 1 | 1 | ||
| Z | 0 | -1 | -2 | |||
Итерация 1
Базисные переменные  | Свободные члены ( ) | Коэффициенты при неизвестных | ||||
 |  |  |  |  | ||
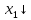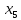 | 6 | -3 | 1 | 2 | ||
 | 2 | -2 | 1 | 1 | ||
 | 1 | 3 | -1 | 1 | ||
| Z | 4 | -5 | 2 | |||
Итерация 2
Базисные переменные 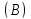 | Свободные члены (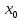 ) | Коэффициенты при неизвестных | ||||
 |  |  |  |  | ||
 | 7 | 1 | 1 | 1 | ||
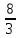 |  | 1 |  |  | ||
 |  | 1 |  |  | ||
| Z |  = 5  |  |  | |||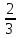
Задача ЛП решена. Решение нецелочиcленное. В таблице (7.3) получен оптимальный план. В столбце 
не все элементы целые. Так как во второй строке в
содержится наибольшая дробная часть, то для нее составляют дополнительное ограничение, коэффициенты которого следующие: 
или 
Добавляем неравенство Гомори к итерации 2. Получим задачу ЦЛП: MaxZ=x1 + 2x2 при условиях: x3 +x4+x5 = 7 x2+
x4+
x5 = 
x1—
x4+
x5= 
— 
x4—
x5 ≤
. 
. Исходная симплексная таблица
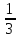
Базисные переменные  | Свободные члены ( ) | Коэффициенты при неизвестных | |||||
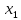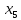 |  |  |  |  | S2 | ||
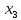 | 7 | 1 | 1 | 1 | |||
 |  | 1 |  |  | |||
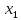 |  | 1 |  |  | |||
 S2 |  |  |  | 1 | |||
| Z |  = 5  |  |  | ||||
Итерация 1
Базисные переменные  | Свободные члены ( ) | Коэффициенты при неизвестных | S2 | |||||
 |  |  |  |  | ||||
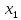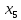 | 5 | 1 | -1 | 3 | ||||
 | 2 | 1 | 1 | |||||
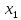 | 1 | 1 |  | -1 | ||||
| S2 | 2 | 1 | 2 | -3 | ||||
| Z | 5 | 1 | 1 | |||||
Получили оптимальное и целочисленное решение 
L(max) = 5. Дадим геометрическую интерпретацию решения данной задачи. Из рис. 1 видно, что максимально значение целевая функция принимает в точке 
, то есть решение
является оптимальным, но без учета требования целочисленности. 
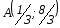
| II |
Рис. 1 С учетом требования целочисленности решение 
не является оптимальным, поэтому используем дополнительное ограничение 
или 
. Значения переменных x4 и x5 подставим из второго и третьего уравнений системы ограничений
,
. В результате получим
. Этому неравенству на рис. 1 соответствует полуплоскость, ограниченная прямой
, отсекающей от многоугольника допустимых решений треугольник АДА*. В новом многоугольнике допустимых решений ОДА*ВС найдем точку А*(1,2), в которой целевая функция принимает максимальное значение. Так как координаты точки А* – целые числа, то решение
является оптимальным планом исходной задачи.
6. Целочисленное линейное программирование
Целочисленное программирование – раздел математического программирования, рассматривающий оптимизационные задачи, в которых все или некоторые переменные могут принимать только целые значения. Как правило, требование целочисленности переменных значительно усложняет задачу. Целочисленное программирование систематически изучается с 1956 года, но и сейчас этот раздел находится в стадии развития.
6.1. Общая постановка задачи целочисленного линейного программирования (зцлп).
Мы будем рассматривать только полностью целочисленные задачи, в которых требование целочисленности наложено на все переменные. Общий вид такой ЗЦЛП отличается от ЗЛП только тем, что ко всем переменным предъявляется требование целочисленности. В частности, в каноническом виде ЗЦЛП ставится так:
(6.1)
Для ЗЦЛП используется та же терминология, что и для ЗЛП: целевая функция, допустимое решение, оптимальное решение и т.д. Если в ЗЦЛП отбросить требование целочисленности, то получится так называемая ослабленная задача. Ослабленная задача является ЗЛП, в то время как ЗЦЛП таковой не является. Дело в том, что требование целочисленности переменных нельзя записать в виде линейного ограничения. Аналитически его записать можно. Действительно, обозначим через [a] целую часть числа а, т.е. наибольшее целое, которое не больше а. Например, [3.4] =3; [-7.2]= -8. Требование целочисленности переменной xj можно записать так: xj -[xj ] =0. Однако это соотношение не является линейным. Таким образом, нельзя сказать, что ЗЦЛП – частный случай ЗЛП – она вообще не является ЗЛП.
Для ЗЦЛП не существует такого универсального эффективного метода решения, каким является симплекс-метод для ЗЛП. Из точных методов решения отметим метод отсечения Гомори и комбинированный метод ветвей и границ. Суть этого комбинированного метода мы изложим.
На практике большинство ЗЦЛП решается приближенно. При этом часто приходится разрабатывать приближенный метод, учитывающий специфические особенности задачи.
6.2. Целочисленная задача об использовании сырья.
Предприятие выпускает n видов штучной продукции стоимостью 
за штуку. Для изготовления продукции используетсяm видов сырья, запасы которого на предприятии равны соответственно
. Известна (m X n) – матрица (aij), в которой 
— расходi – го сырья на производство единицы продукции j –го вида. Требуется составить такой план производства, при котором выручка от реализации продукции была бы наибольшей.
Математическая модель задачи имеет вид:
f =→ max
Здесь — количество продукцииj –го вида.
Это задача целочисленного линейного программирования.
Целочисленность переменных существенна в тех случаях, когда речь идет о производстве дорогостоящей продукции.
6.3. Задача о рюкзаке.
Целочисленная задача об использовании сырья не является ярко выраженной ЗЦЛП. К типичным ЗЦЛП относятся т.н. комбинаторные оптимизационные задачи. В комбинаторных задачах имеется конечное множество вариантов, из которых нужно выбрать оптимальный. Примером такой задачи является задача о рюкзаке.
Имеется рюкзак вместимостью V и n предметов объемами v1, v2 , . vn и стоимостями с1, c2 . c n . Требуется упаковать рюкзак так, чтобы стоимость упакованных предметов была максимальной.
Составим математическую модель этой задачи.
Пусть xj – переменная, принимающая только два значения: 0 или 1, причем xj =0, если j-й предмет не упаковывается в рюкзак; xj = 1, если j-й предмет упаковывается в рюкзак. Тогда задача записывается так:
Это ЗЦЛП, называемая задачей булева программирования. Ограничения задачи можно записать иначе: