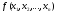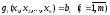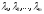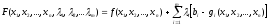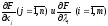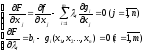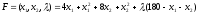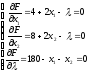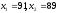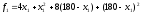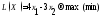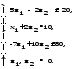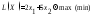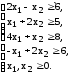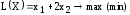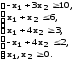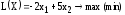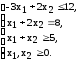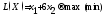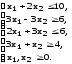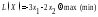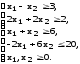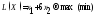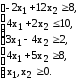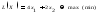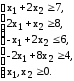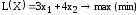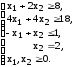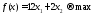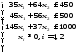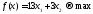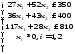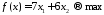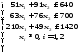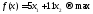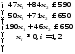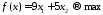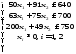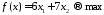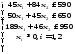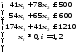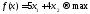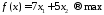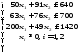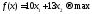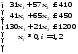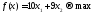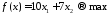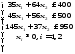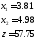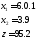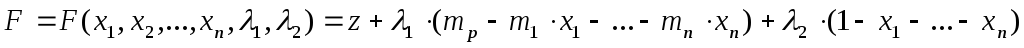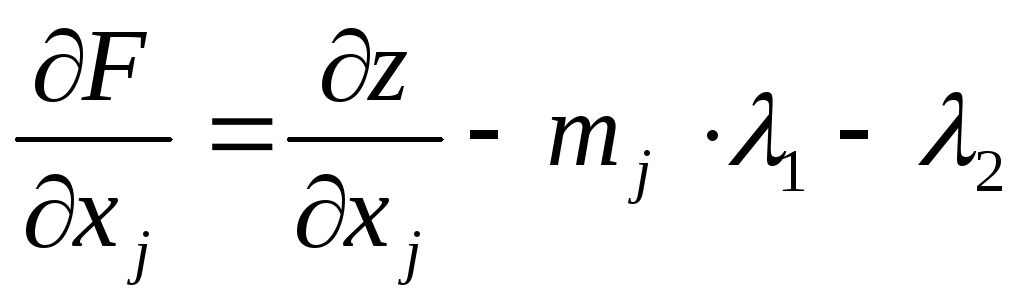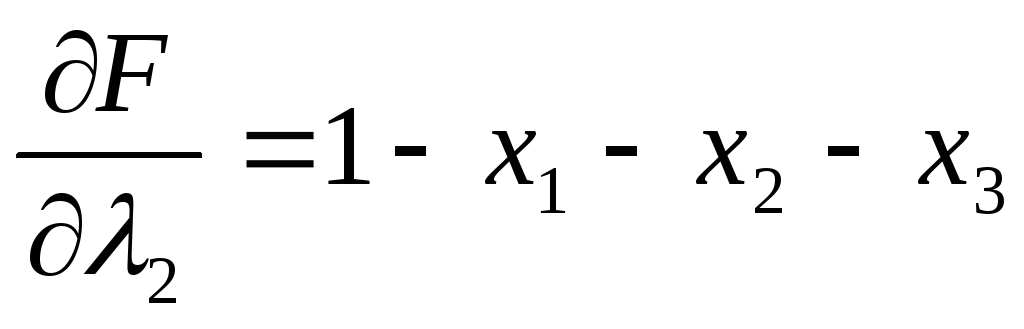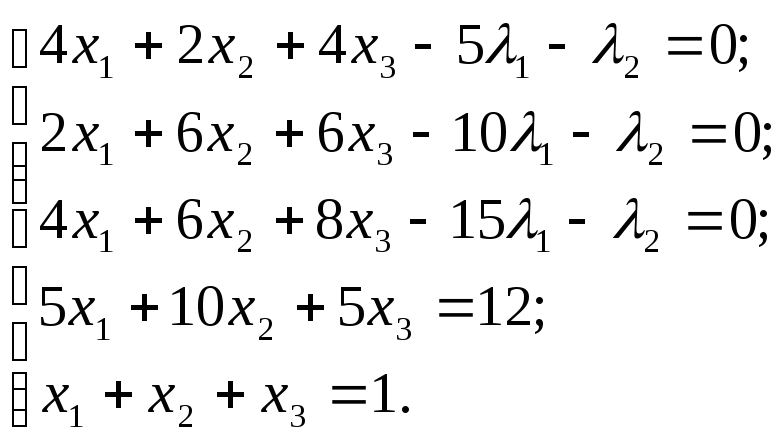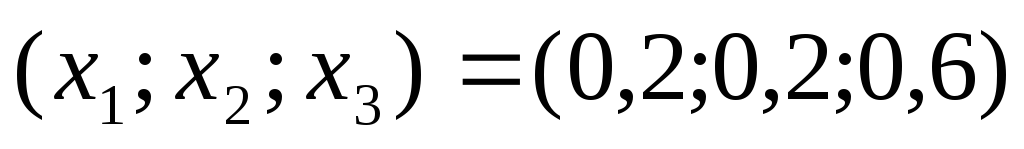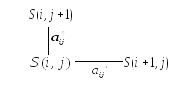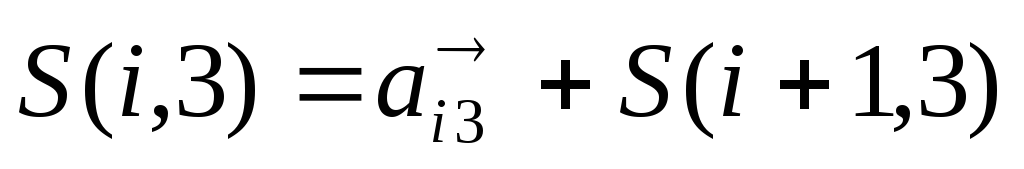Задачи программирования функция лагранжа составить

4.2 Решение задач нелинейного программирования с ограничениями-равенствами

Основными среди точных методов решения задач нелинейного программирования данного типа является метод множителей Лагранжа.

Теорема. Если — точка локального минимума дифференцируемой функции , то при ограничениях , удовлетворяющих некоторому условию регулярности, для функции Лагранжа

существует вектор множителей Лагранжа такой, что

Замечания. 1.Множители Лагранжа имеют произвольные знаки.

2. Если f и выпуклы, то необходимые условия (4.4.), (4.5.) являются и достаточными для существования решения задачи (4.1.), (4.2.).

3. Требование регулярности связано с существованием решения системы (4.4.), (4.5.).

Метод множителей Лагранжа позволяет отыскивать максимум или минимум функции при ограничениях–равенствах, т.е. в (4.1) все ограничения являются равенствами. Основная идея метода заключается в переходе от задачи на условный экстремум к задаче отыскания безусловного экстремума некоторой специально построенной функции Лагранжа.

Составим функцию Лагранжа следующего вида:

Для того чтобы вектор являлся решением задачи (4.6.), (4.7.) , необходимо существование такого вектора , чтобы пара векторов удовлетворяла системе уравнений:

Пример 11. В двух цехах предприятия нужно изготовить 20 изделий некоторой продукции. Затраты, связанные с изготовлением х₁ изделий в 1-м цехе, равны руб., а затраты при изготовлении х₂ изделий во 2-м цехе равны руб. Составить план производства изделий в двух цехах с минимальными затратами.

Решение. Математическая модель задачи:

Для данной точки получим в точке экстремума:

Исследуем характер функции f в окрестности точки , для этого находим

Так как и , то функция выпукла, и точка — точка минимума.

Ответ: Оптимальный план изделий.

4.3. Решение задач нелинейного программирования с ограничениями-неравенствами

Имеется задача нелинейного программирования с ограничениями-неравенствами:

Допустим, что функции и все , выпуклы по Х. Такая задача носит название выпуклого программирования и множество решений , определяемое условиями (4.9), является выпуклым. Для задачи (4.8), (4.9) справедлива теорема Куна-Таккера.

Теорема. Пусть , , обладают непрерывными частными производными на некотором открытом множестве пространства , содержащем . Если является точкой минимума при ограничениях , удовлетворяющих некоторому дополнительному условию регулярности, то существуют такие неотрицательные множители Лагранжа для которых выполняются следующие условия:

Последнее условие называется условием дополняющей нежесткости.

Если функции и — выпуклы по Х, то условия оптимальности (4.10), (4.11) будут не только необходимыми, но и достаточными. В этом случае условие существования решения Х и , удовлетворяющего (4.10), (4.11), которое называют условием регулярности, примет вид

Пользуясь теоремой Куна-Таккера, задачу нелинейного программирования решают следующим образом.

Шаг 1. Составляют функцию Лагранжа

Шаг 2. Составляют систему уравнений вида (4.10), (4.11).

Шаг 3. Находят ее решение . В отличие от задачи с ограничениями-равенствами вектор должен в этом случае удовлетворять условию неотрицательности.

Часто в задачах исследования операций приходится решать задачи, в которых переменные , должны удовлетворять условию .

Основные положения теории могут быть легко распространены на этот случай. Тогда к ограничению (4.9) следует добавить следующее ограничение:

Это ограничение в общем виде можно записать как

Задача представлена в каноническом виде. Применим к ней теорему Куна-Таккера, для чего составим функцию Лагранжа

где — множители, связанные с ограничениями (4.12). Условия теоремы Куна-Таккера выглядят так:

Последнее соотношение представляет собой условия дополняющей нежесткости для ограничений неотрицательности.

Теорема. Пусть задача нелинейного программирования имеет вид

а функции и дифференцируемы и выпуклы по Х. Вектор является оптимальным решением задачи тогда и только тогда, когда существует такой вектор , что пара является седловой точкой функции Лагранжа , т.е. выполняются следующие условия:

Пример 12. Предприятие выпускает два вида изделий А и Б. Норма расхода на производство каждого вида изделий приведены в таблице. При этом известно, что сырья имеется 12 т, а оборудования — 30 станко-часов.

Источник

Метод множителей Лагранжа

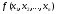
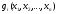
Рассмотрим частный случай общей задачи нелинейного программирования (11), (12), предполагая, что система ограничений (12) содержит только уравнения, отсутствуют условия неотрицательности переменных и и— функции непрерывные вместе со своими частными производными

max(min) (14)

(15)

Данную задачу называют задачей на условный экстремум или классической задачей оптимизации.

Чтобы найти решение этой задачи, вводят набор переменных называемых множителями Лагранжа, составляютфункцию Лагранжа

(16)

находят частные производные и рассматривают системуn+mуравнений

(17)

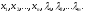
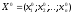
с n+mнеизвестнымиВсякое решение системы уравнений (17) определяет точкув которой может иметь место экстремум функции. Следовательно решив систему уравнений (17), получают все точки, в которых функция (14) может иметь экстремальные значения.

Алгоритм метода множителей Лагранжа

Этап 1.Составляем функцию Лагранжа.

Этап 2.Находим частные производные от функции Лагранжа по переменными приравниваем их нулю.

Этап 3.Решаем систему уравнений (17), находим точки, в которых целевая функция задачи может иметь экстремум.

Этап 4. Среди точек, подозрительных на экстремум, находим такие, в которых достигается экстремум, и вычисляем значения функции (17) в этих точках.

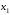
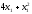
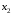
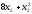
Задача 2. По плану производства продукции предприятию необходимо изготовить 180 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. При производствеизделий 1 способом затраты равныруб., а при изготовленииизделий 2 способом они составляютруб.. Определить сколько изделий каждым из способов следует изготовить, чтобы затраты на производство продукции были минимальными.

Целевая функция для поставленной задачи имеет вид

min при условиях.

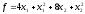
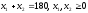
Этап 1. Составляем функцию Лагранжа

.

Этап 2.Вычисляем частные производные пои приравниваем их нулю:

Этап 3.Решая полученную систему уравнений, находим

Этап 4.Сделав замену в целевой функции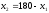, получим функцию от одной переменной, а именно

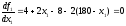
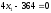
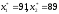
Вычисляем или, откуда имеем. Значение целевой функции равно 17278 руб

Задания для самостоятельной работы

1. Решить задачи линейного программирования графическим методом, симплексным методом с искусственным базисом, методом Гомори

Задача №.2

2. Решить симплексным методом с естественным базисом

Вариант 1 ,

Вариант 2 ,

Вариант 3 ,

Вариант 4 ,

Вариант 5 ,

Вариант 6 ,

Вариант 7 ,

Вариант 8 ,

Вариант 9 ,

Вариант 10 ,

Вариант 11 ,

Вариант 12 ,

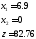
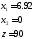
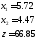
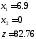
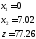
Ответы: 1) 2)3)4)5)6)

7) 8)9)10)11)

Источник

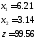
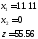
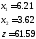
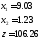
5.2. Решение задачи нелинейного программирования методом множителей Лагранжа

К нелинейным задачам вида (5.1) применим метод множителей Лагранжа.

1. Составим функцию Лагранжа:

.

2. Найдем первые частные производные функции Лагранжа:

, j=1,2,…,n,

, .

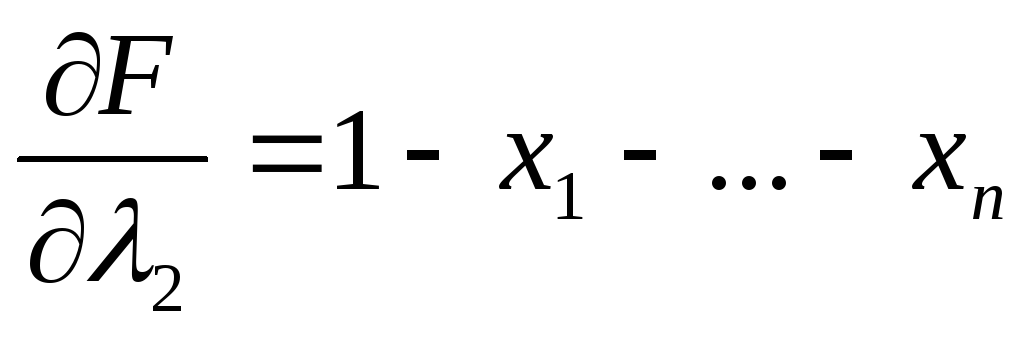
3. Приравняем частные производные к 0; в результате получится система из n+2 уравнений от n+2 переменных:

.

4. Найдем решение системы .

5. Отбросив две последние переменные, получим условный экстремум функции z.

6. На конкретном примере убедимся в том, что найденные значения доставляют исходной функции минимальное значение. Пример 5.2. решить задачу из примера 5.1 методом множителей Лагранжа.

Составляем функцию Лагранжа:

.

Находим частные производные по каждой из переменных:

;;

;

;

.

Приравниваем их к нулю и получаем систему:

.

Отсюда, условным экстремумом исходной функции является вектор

, (5,2)

.

также удовлетворяет системе ограничений исходной задачи. Но . Следовательно, (5,2) – точка минимума.

6. Динамическое программирование

6.1. Принцип оптимальности Беллмана

Этот метод применяется для решения широкого класса задач, в том числе и экономического характера, когда планирование осуществляется в несколько этапов (шагов). Характерной особенностью таких задач является возможность управления рассматриваемым процессом на каждом его этапе. При этом значение целевой функции, которую надо оптимизировать, зависит от последовательности выбираемых на каждом этапе управлений. Динамическое программирование основано на принципе оптимальности Беллмана, согласно которому на любом этапе нужно из нескольких возможных управлений выбирать такое, при котором выигрыш на этом этапе плюс оптимальный суммарный выигрыш на всех последующих этапах был бы максимальным. Этот принцип оптимальности в математической форме можно выразить в виде некоего функционального уравнения, которое необходимо решать на всех этапах, начиная с последнего, причем конкретный вид функционального уравнения Беллмана существенно зависит от специфики рассматриваемой задачи.

6.2. Задача построения оптимального маршрута

Рассмотрим метод динамического программирования на примере задачи построения оптимального маршрута.

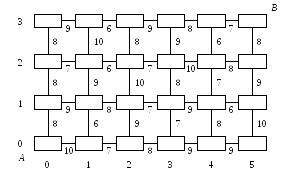
Пример. 6.1. Имеется план строительства дороги между пунктами А и В, на котором для любого промежуточного участка дороги известна предполагаемая стоимость его строительства (рисунок 9):

Требуется построить такой маршрут, соединяющий начальный и конечный пункты, для которого его суммарная стоимость строительства была бы минимальной (маршрут должен проходить только по горизонтальным и вертикальным линиям).

Нарисуем еще раз план строительства, на котором промежуточные пункты изобразим в виде квадратиков (или кружков), куда в процессе решения будут заноситься некоторые числа (рисунок 10):

Пронумеруем вертикальные линии (i = 0,1,2,3,4,5) и горизонтальные (j = 0,1,2,3). Тогда любой промежуточный пункт будет задаваться парой чисел (i, j), что соответствует координатам точки на плоскости (начальный пункт имеет координаты А(0,0), конечный В(5,3)). Обозначим через 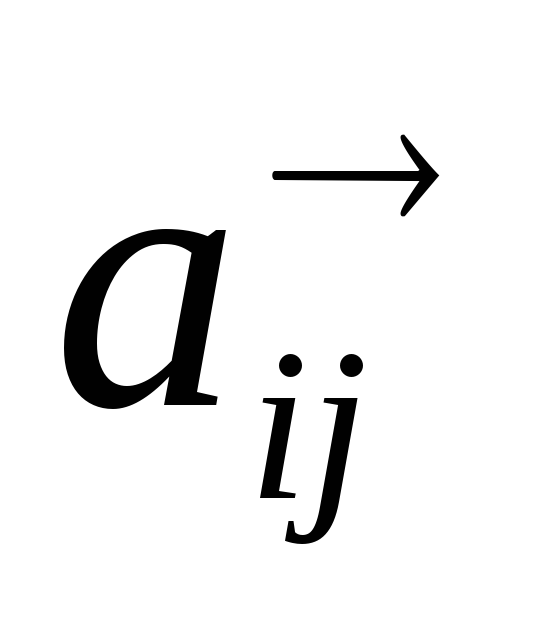, который идет из пункта (i, j) вправо, то есть в пункт (i+1, j), а через — из пункта (i, j) в пункт (i, j+1) (рисунок 11).

Пусть S(i, j) – это минимальная суммарная стоимость строительства маршрута, который идет из пункта (i, j) в конечный пункт В(5,3).

Очевидно, что в любом пункте (i, j) выбор одного из двух возможных направлений, вверх или вправо (это есть управления), должен осуществляться исходя из следующего функционального уравнения Беллмана:

.

2. Определим значения , то есть для верхней строки по формуле

,

двигаясь по верхней строке справа налево:

, ,,,. (в процессе вычислений эти значения сразу заносим в соответствующие квадратики).

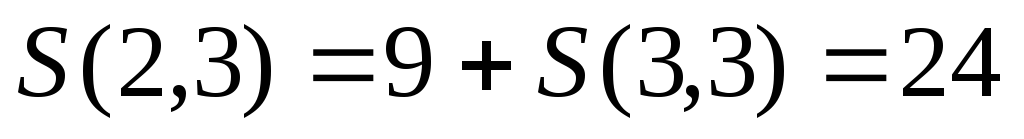
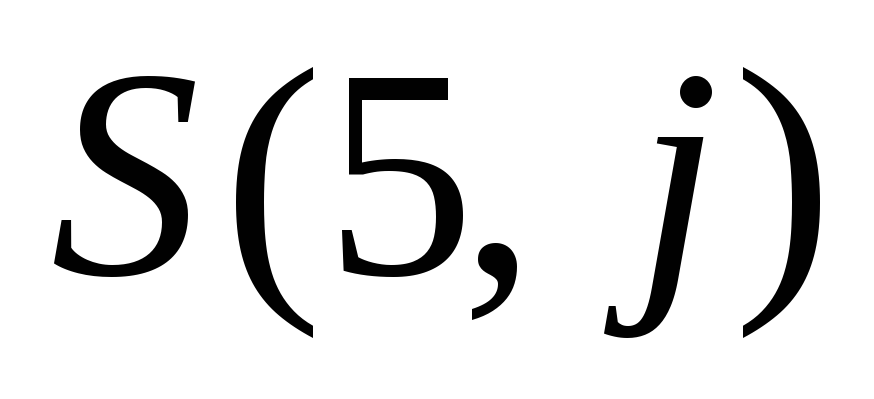
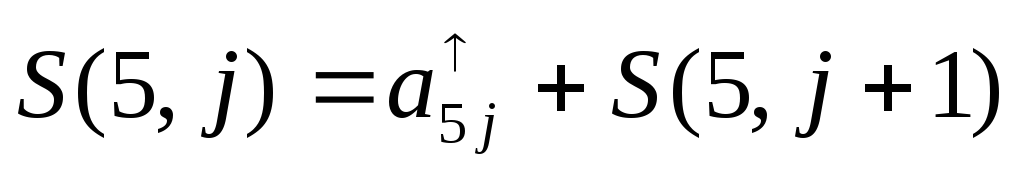
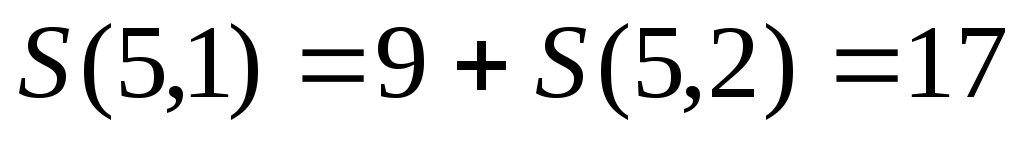
3. Аналогично определим значения , то есть для крайнего правого столбца двигаясь сверху вниз, по формуле:,,,.

4. Далее, определим все остальные значения S(i, j) пользуясь функциональным уравнением Беллмана, двигаясь справа налево и сверху вниз: ,,,, …, и т.д..

5. Заносим все вычисления в соответствующие квадратики (рисунок 12);

таким образом, самый дешевый маршрут имеет стоимость ;

Теперь построим этот оптимальный маршрут, двигаясь уже в направлении от А к В и выбирая в каждом промежуточном пункте то направление (вправо или вверх), которое соответствует минимуму в функциональном уравнении Беллмана (на рисунке этот оптимальный маршрут выделяется пунктирной линией).

Может случится так, что в некоторых промежуточных пунктах придется выбирать минимальное из двух одинаковых чисел. Это означает, что в этом пункте можно выбирать любое из двух направлений, т.е. оптимальных маршрутов может быть несколько.

Источник