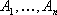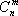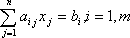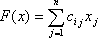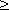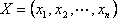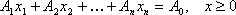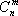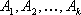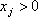Задачи положительного линейного программирования

2. Задача об оптимальном использовании ресурсов при производственном планировании.

Общий смысл задач этого класса сводится к следующему.

Предприятие выпускает n различных изделий. Для их производства требуется m различных видов ресурсов (сырья, материалов, рабочего времени и т.п.). Ресурсы ограничены, их запасы в планируемый период составляют, соответственно, b₁, b₂. b_m условных единиц.

Известны также технологические коэффициенты a_ij, которые показывают, сколько единиц i-го ресурса требуется для производства единицы изделия j-го вида ( ).

Прибыль, получаемая предприятием при реализации изделия j-го вида, равна c_j.

В планируемом периоде значения величин a_ij, b_i и c_j остаются постоянными.

Требуется составить такой план выпуска продукции, при реализации которого прибыль преприятия была бы наибольшей.

Далее приведем простой пример задачи такого класса.

Компания специализируется на выпуске хоккейных клюшек и наборов шахмат. Каждая клюшка приносит компании прибыль в размере $2, а каждый шахматный набор — в размере $4. На изготовление одной клюшки требуется четыре часа работы на участке A и два часа работы на участке B. Шахматный набор изготавливается с затратами шести часов на участке A, шести часов на участке B и одного часа на участке C. Доступная производственная мощность участка A составляет 120 н-часов в день, участка В — 72 н-часа и участка С — 10 н-часов.

Сколько клюшек и шахматных наборов должна выпускать компания ежедневно, чтобы получать максимальную прибыль?

Условия задач указанного класса часто представляют в табличной форме (см. таблицу 2.1).

Таблица 2.1 — Исходные данные задачи об использовании производственных ресурсов

производственные участки

затраты времени на единицу продукции, н-час

доступный фонд времени, н-час

Источник

Общая задача линейного программирования.

3) цель задачи ()

(max F(x))

(min F(x))

Определение: Планом или допустимым решением задачи линейного программирования называется вектор , удовлетворяющий условиям 1) и 2)

(*)

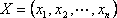
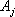
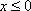
Определение: План называетсяопорным, если векторы , входящие в разложение (*) с положительными коэффициентами, являются линейно независимыми.

Определение: Опорный план называется невырожденным, если он содержит m – положительных компонентов, в противном случае опорный план называется вырожденным.

Определение: Оптимальным планом (решением) задачи линейного программирования называется план, доставляющий линейной форме наибольшее или наименьшее значение.

В большинстве задач ограничения задаются не в виде системы уравнений, а в виде системы линейных неравенств, либо система ограничений смешанная, однако любую систему ограничений можно привести к системе уравнений. Для этого достаточно к левой части каждого неравенства прибавить (для ) или отнять (для) какое-то неотрицательное число (добавочную переменную) с тем, чтобы каждое неравенство обратилось в уравнение, в результате получим эквивалентные системы уравнений и неравенств.

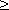
Основные теоремы линейного программирования

Теорема 1: Множество всех допустимых решений системы ограничений задачи линейного программирования, является выпуклым.

Теорема 2: Если существует, и при том единственное, оптимальное решение задачи линейного программирования, то оно совпадает с одной из угловых точек множества допустимых решений. Если линейная форма принимает минимальное (максимальное) значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.

Из теоремы 2 следует, что поиски оптимального решения можно ограничить перебором конечного числа угловых точек (их число меньше , гдеn — число неизвестных , а m – число ограничений), однако построение возможно только для двух и трёхмерных пространств, поэтому нужны аналитические методы, позволяющие находить координаты угловых точек.

Теорема 3: Если известно, что система векторов в разложении линейно независима и такова, что, где, то точкаявляется угловой точкой многогранника решений.

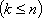
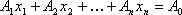
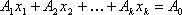
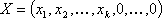
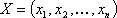
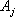
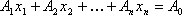
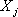
Теорема 4: Если — угловая точка многогранника решений, то векторыв разложении, соответствующие положительным, являются линейно независимыми.

Следствие 1: Так как векторы 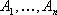имеют размерностьm, то угловая точка многогранника решений имеет не более m положительных компонент .

Следствие 2: Каждой угловой точке многогранника решений соответствует линейно независимых векторов системы векторов.

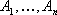
Симплексный метод решения задачи линейного программирования.

Доказано, что оптимальное решение задачи линейного программирования связано с угловыми точками многоугольника решений, то есть с опорными планами. Они определяются системой m — линейно независимых векторов, содержащихся в системе из n — векторов. Количество опорных планов меньше, гдеn — число неизвестных, а m – число ограничений. При больших n и m найти все их перебором очень трудно, поэтому необходимо упорядоченный перебор, такой схемой является симплексный метод, который позволяет исходя из известного опорного плана задачи, за конечное число шагов получить её оптимальный план. Каждый из шагов (итераций) состоит в нахождении нового плана, которому соответствует меньшее для задачи на минимум (большее для задачи на максимум) значение линейной формы, чем её значение в предыдущем плане. Процесс продолжается до получения оптимального плана. Если задача не обладает планами или её линейная форма неограниченна на многограннике решений, то симплексный метод позволяет установить это в процессе решения.

Источник