Организация решения задач динамического программирования
Имомов, А. И. Организация решения задач динамического программирования / А. И. Имомов, Э. Р. Бокиев. — Текст : непосредственный // Молодой ученый. — 2015. — № 12 (92). — С. 1-6. — URL: https://moluch.ru/archive/92/20036/ (дата обращения: 20.07.2023).
Основная цель работы — показать, как решаются три задачи динамического программирования: оптимальная замена оборудования, оптимальное распределение ресурсов, минимизация затрат на строительство и эксплуатацию предприятий.
Ключевые слова: динамическое программирование, задачи оптимальной стратегии замены оборудования, оптимального распределения ресурсов, минимизации затрат на строительство и эксплуатацию предприятий.
Математическая наука, занимающаяся изучением экстремальных задач управления, планирования и разработкой методов их решения, называется исследованием операций.
Динамическое программирование — один из разделов исследования операций, в котором процесс принятия решения и управления может быть разбит на отдельные этапы.
Одним из основных методов динамического программирования является метод функциональных уравнений Р.Беллмана [1–4], который основывается на использовании его же принципа оптимальности. Принцип состоит в том, что, каковы бы ни были начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придет система в конце данного шага. Использование данного принципа гарантирует, что управление, выбранное на любом шаге, не локально лучше, а лучше с точки зрения процесса в целом.
В задачах, решаемых методом динамического программирования, процесс управления разбивается на шаги. При распределении на несколько лет ресурсов деятельности предприятия шагом целесообразно считать временной период; при распределении средств между предприятиями — номер очередного предприятия. В других задачах разбиение на шаги вводится искусственно. Например, непрерывный управляемый процесс можно рассматривать как дискретный, условно разбив его на временные отрезки.
В данной статье решаются три задачи динамического программирования из книги [1].
2.1. Оптимальная стратегия замены оборудования.
Одной из важных экономических задач является определение оптимальной стратегии в замене старых станков, агрегатов, машин на новые. Старение оборудования включает его физический и моральный износ, в результате чего увеличиваются производственные затраты по выпуску продукции на старом оборудовании, увеличиваются затраты на его ремонт и обслуживание, снижаются производительность и ликвидная стоимость.
Наступает время, когда старое оборудование выгоднее продать, заменить новым, чем эксплуатировать ценой больших затрат; причем его можно заменить более совершенным новым оборудованием. Оптимальная стратегия замены оборудования состоит в определении оптимальных сроков замены. Критерием оптимальности при этом может служить прибыль от эксплуатации оборудования, которую следует оптимизировать, или суммарные затраты на эксплуатацию в течение рассматриваемого промежутка времени, подлежащие минимизации.
Введем обозначения: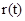 
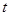
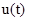
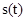
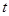
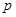
— стоимость продукции, производимой за один год на единице оборудования возраста 
лет; аналогично, 
и 
— ежегодные затраты на обслуживание и остаточная стоимость оборудования возраста 
лет; 
— покупная цена оборудования.
Рассмотрим период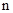 
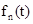
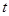
лет, в пределах которого требуется определить оптимальный цикл замены оборудования. Обозначим через 
максимальный доход, получаемый от оборудования возраста лет за оставшиеся n лет цикла использования оборудования при условии оптимальной стратегии.
Возраст оборудования отсчитывается в направлении течения процесса. Так,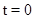 
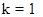
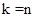
соответствует случаю использования нового оборудования. Временные этапы процесса нумеруются в обратном направлении по отношению к ходу процесса. Так, 
относится к одному временному этапу, остающейся до завершения процесса, а 
— к началу процесса:
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
В ряде реальных экономических и производственных задач необходимо учитывать изменение моделируемого процесса во времени и влияние времени на критерий оптимальности. Для решения указанных задач используется метод динамического планирования (динамическое программирование). Этот метод более сложен по сравнению с методами расчета статических оптимизационных задач, изложенных выше. Также не простым делом является процесс построения для реальной задачи математической модели динамического программирования.
§ 3. Задачи динамического программирования.
3.1. Основные условия и область применения задач динамического программирования Пусть рассматривается задача, распадающаяся на т шагов или этапов, например планирование деятельности предприятия на несколько лет, поэтапное планирование инвестиций, управление производственными мощностями в течение длительного срока. Показатель эффективности задачи в целом обозначим через B , а
| показатели эффективности на отдельных шагах — через | f i , i = | 1, m | . |
| Если B обладает свойством аддитивности, т.е. | |||
| m | |||
| B = ∑ f i ( x i ) , | (3.1) | ||
| i = 1 | |||
то можно найти оптимальное решение задачи методом динамического программирования. Таким образом, динамическое программирование — это метод оптимизации многошаговых или многоэтапных процессов, критерий эффективности которых обладает свойством (3.1). В задачах динамического программирования критерий эффективности называется выигрышем. Данные процессы управляемые, и от правильного выбора управления зависит величина выигрыша. Переменная x i , от которой зависят выигрыш на i -м шаге и, следовательно, выигрыш в целом, называется шаговым управлением , i = 1, m . Управлением процесса в целом ( x ) называется последовательность шаговых управлений x = ( x 1 , x 2 . x m ) . Оптимальное управление x — это значение управления x , при котором значение B ( x ) является максимальным (или минимальным,
| если требуется уменьшить проигрыш) | |
| B = B ( x ) = max < B ( x ) >, x X , | (3.2) |
где X ─ область допустимых управлений. Оптимальное управление x определяется последовательностью оптимальных шаговых управлений x = ( x 1 , x 2 . x m ) . В основе метода динамического программирования лежит принцип оптимальности Беллмана, формулирующийся следующим образом: управление на каждом шаге надо выбирать так, чтобы оптимальной была сумма выигрышей на всех оставшихся до конца процесса шагах, включая выигрыш на данном шаге. Поясним это правило. При решении задачи динамического программирования на каждом шаге выбирается управление, которое должно привести к оптимальному выигрышу. Если считать все шаги независимыми друг от друга, то оптимальным шаговым управлением будет то управление, которое приносит максимальный выигрыш именно на данном шаге. Но, например, при покупке новой техники взамен устаревшей на ее приобретение затрачиваются определенные
средства. Поэтому прибыль от ее эксплуатации вначале может быть небольшой. Однако в следующие годы новая техника будет приносить большую прибыль. И наоборот, если руководитель примет решение оставить старую технику для получения прибыли в текущем году, то в дальнейшем это приведет к значительным убыткам. Данный пример демонстрирует следующий факт: в многошаговых процессах все шаги зависят друг от друга, и, следовательно, управление на каждом конкретном шаге надо выбирать с учетом его будущих воздействий на весь процесс. Другой момент, который следует учитывать при выборе управления на данном шаге, — это возможные варианты окончания предыдущего шага. Эти варианты определяют состояние процесса. Например, при определении количества средств, вкладываемых в предприятие в i -м году, необходимо знать, сколько средств осталось в наличии к этому году и какая прибыль получена в предыдущем ( i − 1)- м году. Таким образом, при выборе шагового управления необходимо учитывать: 1) возможные исходы предыдущего шага и 2) влияние управления на все оставшиеся до конца процесса шаги. В задачах динамического программирования первый пункт учитывают, делая на каждом шаге условные предположения о возможных вариантах окончания предыдущего шага и проводя для каждого из вариантов условную оптимизацию. Выполнение второго пункта обеспечивается тем, что в задачах динамического программирования условная оптимизация проводится от конца процесса к началу. Сперва оптимизируется последний m -й шаг, на котором не надо учитывать возможные воздействия выбранного управления x m на все последующие шаги, так как эти шаги просто отсутствуют. Делая предположения об условиях окончания ( m − 1)-го шага, для каждого из них проводят условную оптимизацию m -го шага и определяют условное оптимальное управление x m . Аналогично поступают для ( m − 1)-гo шага, делая предположения об исходах окончания ( m − 2 )-го шага и определяя условное оптимальное управление на ( m − 1)-м шаге, приносящее оптимальный выигрыш на двух последних шагах — ( m − 1)-м и m — м . Так же действуют на всех остальных шагах до первого. На первом шаге, как правило, не надо делать условных предположений, так как состояние системы перед первым шагом обычно известно. Для этого состояния выбирают оптимальное шаговое управление, обеспечивающее оптимальный выигрыш на первом и всех последующих шагах. Это управление является безусловным
оптимальным управлением на первом шаге и, зная его, определяются оптимальное значение выигрыша и безусловные оптимальные управления на всех шагах. Ниже это будет пояснено на примерах. 3.2. Составление математической модели динамического программирования Дополнительно введем следующие условные обозначения: s — состояние процесса; S i — множество возможных состояний процесса перед i -м шагом; B i — выигрыш с 1-го шага до конца процесса, i = 1, m . Можно определить следующие основные этапы составления математической модели задачи динамического программирования. 1. Разбиение задачи на шаги (этапы). Шаг не должен быть слишком мелким, чтобы не проводить лишних расчетов и не должен быть слишком большим, усложняющим процесс шаговой оптимизации. 2. Выбор переменных, характеризующих состояние s моделируемого процесса перед каждым шагом, и выявление налагаемых на них ограничений. В качестве таких переменных следует брать факторы, представляющие интерес для исследователя, например годовую прибыль при планировании деятельности предприятия. 3. Определение множества шаговых управлений x i , i = 1, m , и налагаемых на них ограничений, т.е. области допустимых управлений X . 4. Определение выигрыша
| f i ( s , x i ) , | (3.3) |
который принесет на i -м шаге управление x i , если система перед этим находилась в состоянии s .
| 5. Определение состояния s ‘ , в которое переходит | система из |
| состояния s под влиянием управления x i : | |
| s ‘ = ϕ i ( s , x i ) , | (3.4) |
где ϕ i , — функция перехода на i -м шаге из состояния s в состояние s ‘ .