Задачи оптимизации задача математического программирования

Введение

Необходимость принятия наилучших и обоснованных решений в задачах управления персоналом, распределения материальных и технических ресурсов является неотъемлемой составляющей профессиональной деятельности любого руководящего сотрудника.

Необходимость принятия наилучших решений так же стара, как само человечество. Испокон веку люди, приступая к осуществлению своих мероприятий, раздумывали над их возможными последствиями и принимали решения, выбирая тем или другим образом зависящие от них параметры – способы организации мероприятий. В современной ситуации, в большинстве управленческих задач, решения уже не могут приниматься без специального математического анализа, просто на основе опыта и здравого смысла.

Например, предприятию необходимо организовать бесперебойные поставки товаров со складов производителей в супермаркеты торговой сети автомобильным грузовым транспортом. Для этого требуется ответить на ряд вопросов, например: какое количество автомобилей и какой грузоподъёмности необходимо и достаточно? По каким маршрутам и в какое время суток должны двигаться автомобили? Какие виды товаров, в какие супермаркеты должны поставляться с каждого из складов, с учётом потребностей супермаркетов и объёмов запасов на складах? И так далее. В силу сложности явления, последствия решения каждого из подобных вопросов не столь ясны; для того, чтобы представить себе эти последствия, нужно провести расчеты. Эффективность решения этих и других вопросов напрямую отражается на деловой репутации, финансовом состоянии предприятия и его сотрудников.

В настоящее время менеджер может использовать при принятии решения различные компьютерные и математические средства. В памяти компьютеров могут содержаться большие массивы информации, организованные с помощью систем управления базами данных и других программных продуктов, позволяющих оперативно ею пользоваться. Экономико-математические и эконометрические модели позволяют просчитывать последствия тех или иных решений, прогнозировать развитие событий. Методы экспертных оценок, также весьма математизированы и используют средства вычислительной техники. Наиболее часто используются оптимизационные модели принятия решений.

Реальные прикладные задачи оптимизации очень сложны. Современные методы оптимизации далеко не всегда справляются с решением реальных задач без помощи человека. Нет, пока такой теории, которая учла бы любые особенности функций, описывающих постановку задачи. Следует отдавать предпочтение таким методам, которыми проще управлять в процессе решения задачи.

Математический аппарат для решения задач оптимизации Понятие математического программирования

Математическое программирование – это математическая дисциплина, в которой разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями.

Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах математического программирования оказываются непригодными.

Для решения задач математического программирования разработаны и разрабатываются специальные методы и теории. Так как при решении этих задач приходится выполнять значительный объем вычислений, то при сравнительной оценке методов большое значение придается эффективности и удобству их реализации на ЭВМ.

Математическое программирование можно рассматривать как совокупность самостоятельных разделов, занимающихся изучением и разработкой методов решения определенных классов задач.

В зависимости от свойств целевой функции и функции ограничений все задачи математического программирования делятся на два основных класса:

Если целевая функция и функции ограничений – линейные функции, то соответствующая задача поиска экстремума является задачей линейного программирования. Если хотя бы одна из указанных функций нелинейна, то соответствующая задача поиска экстремума является задачей нелинейного программирования.

Источник

Тема2. Математическое программирование

2.1. Постановка задачи математического программирования. Виды экстремума функций многих переменных

К задачам математического программирования относятся задачи оптимизации, в которых отыскивается экстремум заданной скалярной функции многих переменных при ограничениях в форме системы равенств и неравенств. Все они с формальной точки зрения могут быть сведены к следующей постановке: найти значения переменных 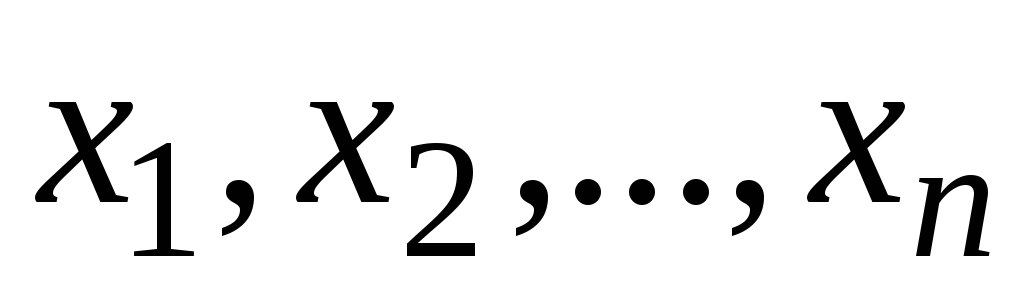,доставляющие экстремальное значения некоторой функции и удовлетворяющие уравнениям и неравенствам

. (2.1)

Предполагается что функции и известны, а – заданные постоянные величины. Условия (2.1) называются ограничениями. Как правило, отдельно оговариваются ограничения на знак переменных , так как методы их учета могут быть иными, чем сложных ограничений типа (2.1). Могут налагаться условия целочисленности переменных. Кратко условия задачи математического программирования можно записывать следующим образом

.

Если при определении экстремума ограничиться рассмотрением минимизации, задача не теряет общности, так как максимизация функции эквивалентна минимизации функции .

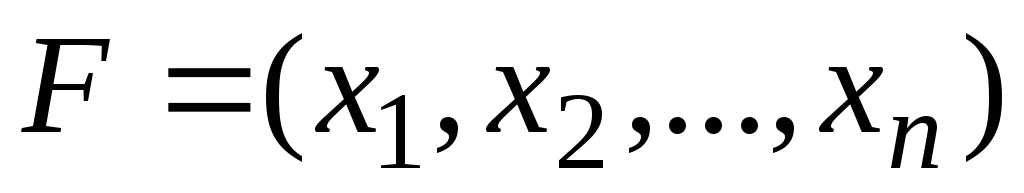
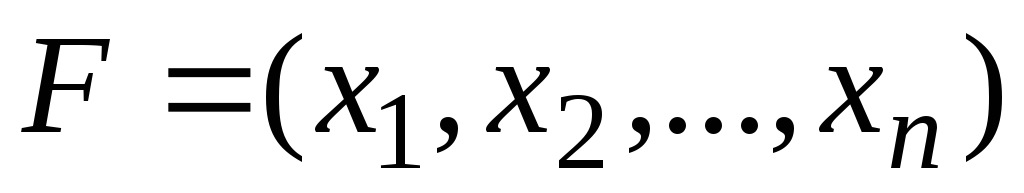
Функция называетсяцелевой функциейилифункциейцели. Переменные , удовлетворяющие совокупности заданных ограничений, представляют собой допустимое решение задачи, и называются планом задачи. Допустимое решение, доставляющие экстремум функции цели , называется оптимальным решением или оптимальным планом. Не каждая задача математического программирования имеет планы, так как не каждая система ограничений имеет решение.

Рассмотрим основные виды экстремума функций конечного числа переменных. Пусть определена в некоторой области переменных . Если на переменные не накладывается никаких ограничений, т.е. область не ограничена, то экстремум функции называется безусловным, а в противном случаеусловным.

Простейшая задача оптимизации связана с нахождением значений переменных, обеспечивающих экстремум функции цели при отсутствии ограничений, т.е. с нахождением безусловного экстремума функции.

Безусловным глобальным минимумом (максимумом)функции называется наименьшее (наибольшее) в пределах всей рассматриваемой областиRзначение этой функции. Если в некоторой точке функция имеет меньшее (большее) значение, чем во всех точках , принадлежащих некоторой малой окрестности точки , то говорят, что в этой точке имеет местолокальный минимум(максимум) функции .

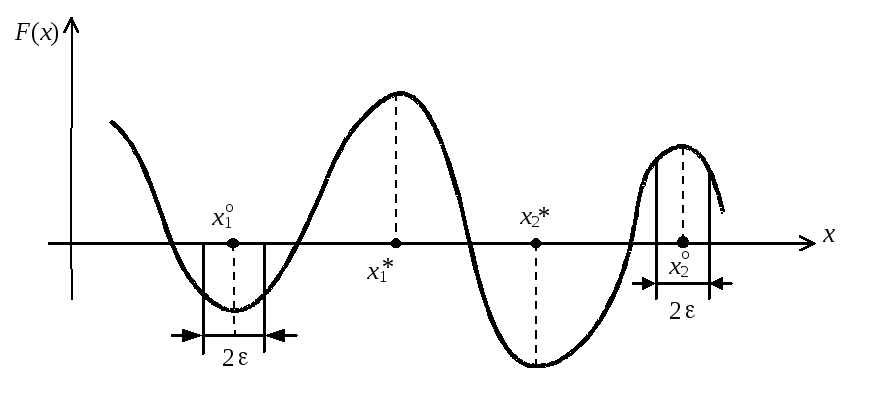
На рис. 2.1, а изображена функция , заданная на неограниченной областиR, здесь в точках и достигается соответственно глобальный безусловный максимум и минимум функции , так как

и для .

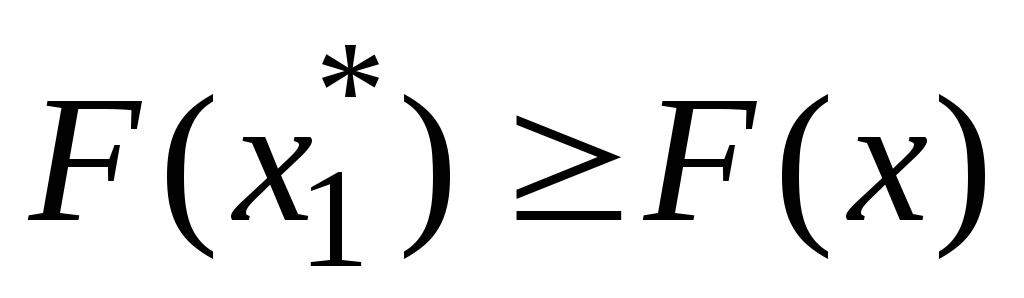
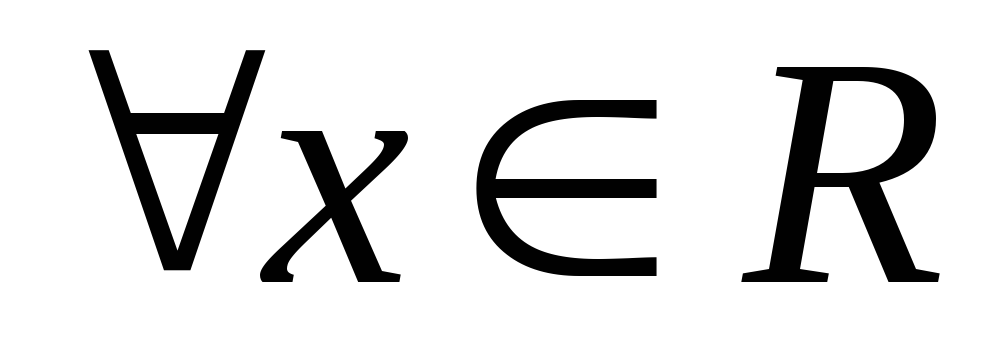
В точках и достигается безусловный локальный минимум и максимум функции , так как в окрестностях этих точек удовлетворяются условия

, ,

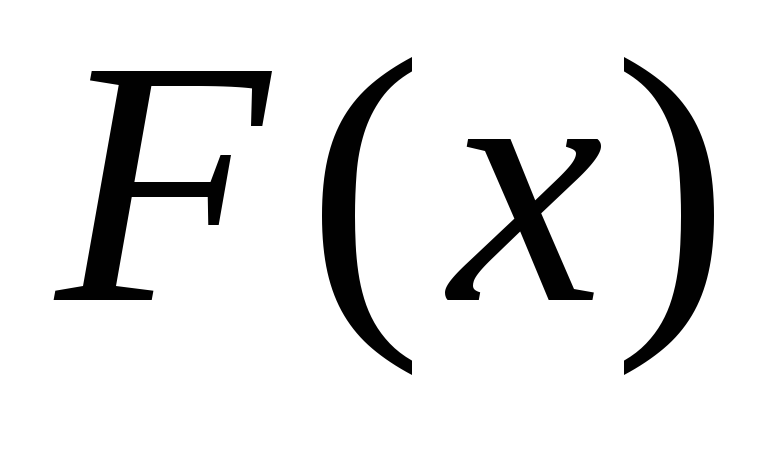
Очевидно, что если в пределах область Rимеется всего один минимум (максимум), то он является глобальным.

При наличии ограничений область Rограничивается областью допустимых значений переменныхX. В этом случае точки экстремума должны обязательно принадлежать областиXи сам экстремум называется условным. При этом экстремумы называютсяграничными, если они имеют место в граничных точках области ивнутренними, если соответствует внутренним точкам областиX.

На рис. 2.1, б область ограничена значениями . Точке здесь будет соответствовать условный глобальный минимум функции , а точкам и условный локальный и глобальный максимум соответственно. Причём экстремумы в точках и являются граничными. В практических задачах наибольший интерес представляет нахождение глобального условного экстремума.

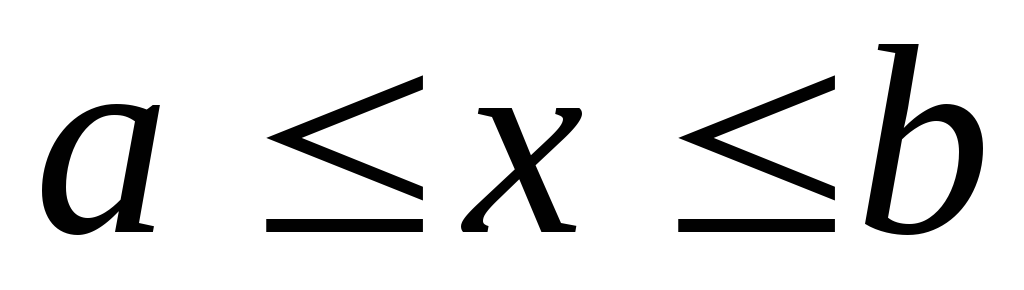
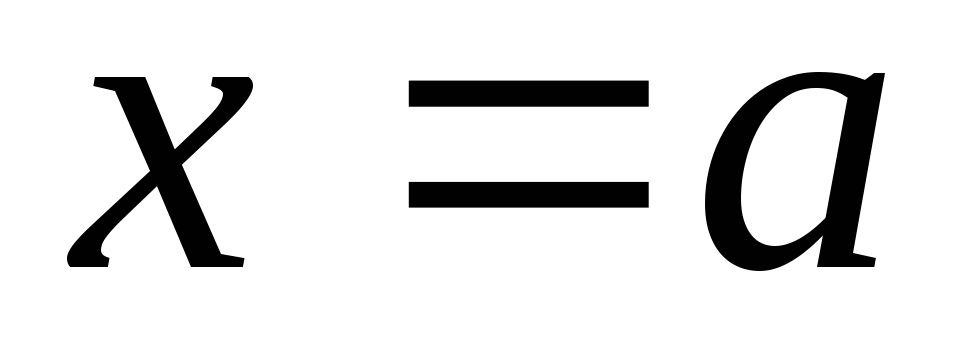
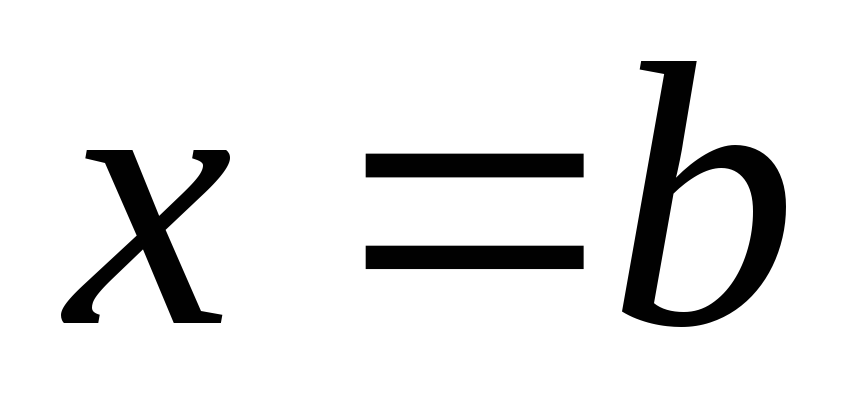
а

б

.

рис. 2.1. Примеры экстремума функции одной переменной:

а – безусловные; б – условные

Источник

Задачи оптимизации и методы их решения

Найти , где – векторный аргумент, по которому ведется оптимизация,– область допустимых значений,– целевая функция. Введем обозначения: , где — оптимальное значение целевой функции,— значение аргумента, при котором определяется. Постановка задачи минимизации или максимизации не нарушает общности: – определяется функциями ограничения: , где — ограничения неравенства, а— ограничения равенства.

Классификация разделов математического программирования

1. Линейное программирование (ЛП) – раздел математического программирования, изучающий задачу поиска минимальной (максимальной) линейной функции при линейных ограничениях в виде равенств или неравенств.
2. Нелинейное программирование – раздел математического программирования, изучающий методы решения и характер экстремума в задачах оптимизации с нелинейной целевой функцией и (или) нелинейными ограничениями.
3. Стохастическое программирование — раздел математического программирования, изучающий модели выбора оптимальных решений в ситуациях, характеризуемых случайными величинами.

Разделы математического программирования

1. Целочисленное программирование — решает задачи оптимизации, в которых на значения переменных наложено требование целочисленности.
2. Квадратичное программирование — решает задачи оптимизации с квадратичной целевой функцией и линейными ограничениями.
3. Геометрическое программирование – решает задачи оптимизации, в которых целевая функция и ограничения представляют собой обобщенные многочлены с положительными коэффициентами.
4. Сепарабельное программирование — решает задачи оптимизации с сепарабельной целевой функцией и сепарабельными ограничениями.
5. Дробно-линейное программирование — решает задачи оптимизации с дробно-линейной целевой функцией и линейными ограничениями.

Источник