Как решать простые задачи оптимизации на питоне с помощью cvxpy
Всем доброго времени суток! Простым поиском я не сумел обнаружить упоминание модуля cvxpy и потому решил написать обучающий материал по нему – просто примеры кода, по которым в дальнейшем новичку будет проще использовать этот модуль для своих задач. cvxpy предназначен для решения задач оптимизации – нахождения минимумов/максимумов функций при определённых ограничениях. Если вам интересна эта тема – прошу под кат.
Общая постановка задачи
Здесь x – независимая переменная (в общем случае вектор), f(x)
целевая функция, которую нужно оптимизировать. Ограничения на область определения f(x) могут быть заданы при помощи равенств и неравенств.
Пример задачи
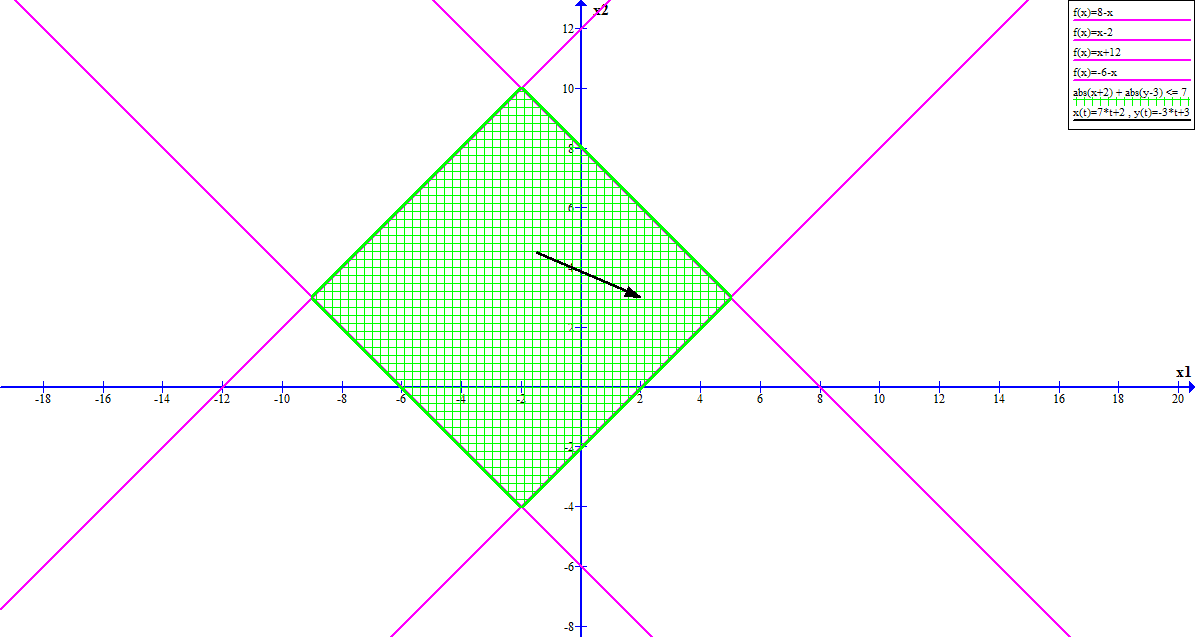
Давайте рассмотрим следующую задачу линейного программирования:
Если посмотреть на область, заданную неравенством с модулем, то можно увидеть что эта область легко может быть задана при помощи линейных неравенств:
В нашем случае ограничения будут следующими:
Решение задачи посредством cvxpy
О установке модуля подробно рассказано на сайте модуля. Давайте напишем простой код, который позволит нам решить нашу тестовую задачу оптимизации:
import numpy as np import cvxpy as cvx # наши независимые переменные x = cvx.Variable(2) A = np.array([[1, 1], [1, -1], [-1, 1], [-1, -1]]) b = np.array([8, 2, 12, 6]) c = np.array([7, -3]) # ограничения constraints = [A * x Наше текущее решение нецелое и выходит за ограничения, однако видно что оно лежит рядом с оптимальным решением (-9, 3). В cvxpy можно использовать разные решатели для решения задачи, подбирая лучший. Давайте попробуем GLPK:
prob.solve(solver = "GLPK") print(prob.status) # optimal print(prob.value) # -72.0 print(x.value) # [[-9.] [ 3.]]Список доступных решателей возвращает функция installed_solvers() .
Другие примеры
Можно решать не только задачи линейного программирования. Давайте рассмотрим исходную формулировку задачи:
# ограничения constraints = [cvx.abs(x[0] + 2) + cvx.abs(x[1] - 3) Также можно искать решение для метода наименьших квадратов:
# целевая функция и что с ней делать obj = cvx.Minimize(cvx.norm(A * x - b)) # по умолчанию используется вторая норма # формулируем задачу и решаем prob = cvx.Problem(obj) prob.solve() print(prob.status) # optimal print(prob.value) # 13.9999999869 print(x.value) # [[-2.] [ 3.]]Конечно, некоторые задачи могут иметь тривиальное решение:
A = np.array([[1, 1], [1, -1], [-1, 1]]) b = np.array([8, 2, 12]) c = np.array([7, -3]) # ограничения constraints = [A * x А некоторые могут не иметь решения вовсе:
A = np.array([[1, 1], [1, -1], [-1, 1], [-1, -1]]) b = np.array([-6, -12, -2, -8]) # ограничения constraints = [A * x Решаем задачу сетевого планирования с помощью Python
Приветствую, меня зовут Алёна. Недавно на математический основах информатики в университете мы проходили задачу сетевого планирования, с помощью которой можно смоделировать процесс производства изделий. Мне была интересна данная тема и я решила поделиться с вами, как решить задачу сетевого планирования с использованием языка Python.
Определения
Сетевая модель — сетевой график, элементами которого (вершинами / дугами / и тем и другим) поставлены в соответствие некоторые величины, называемые весами.
С помощью сетевой модели будем моделировать процесс производства некоторого нового изделия. Вершины будут соответствовать моментам начала или окончания выполнения работ, дуги будут соответствовать условиям взаимозависимости выполняемых работ, а веса на дугах будут соответствовать ожидаемым длительностям выполнения работ.
Суть задачи: требуется определить минимально возможное время, за которое можно выполнить все работы.
Терминология
- i - номер работы
- t(i) - длительность выполнения работы i
- K(i) — множество работ, предшествующих работе с номером i
Для решения задачи пользуются специальной схемой расчета временных характеристик, позволяющей не только дать ответ на поставленный вопрос, но и найти дополнительные характеристики, позволяющие более эффективно управлять процессом изготовления нового изделия.
К таким характеристикам относятся:
- t(rn, i) - время самого раннего начала выполнения работы с номером i
- t(rk, i) - время самого раннего окончания выполнения работы с номером i
- t(pn, i) - время самого позднего начала выполнения работы с номером i
- t(pk, i) - время самого позднего окончания выполнения работы с номером i
- r(i) - резерв времени работы с номером i , т.е. время, на которое не в ущерб времени общего окончания выполнения всех работ, можно задерживать выполнение работы с номером i
- T(k) - время выполнения всех работ изделия. T(k) - длина критического пути, а критическим путём называют путь, соединяющий некоторую начальную работу - не имеющую предшествующих работ, и некоторую конечную работу - не имеющую последующих, т.е. от неё зависящих работ, суммарное время выполнения всех работ которого максимально.
Формулы
Для расчета временных характеристик будем пользоваться следующими формулами:
- t(rn,i) = 0, если K(i) - пустое множество.
- t(rk,i) = t(rn,i) + t(i)t(rn,i)= max t(rk,j), где максимум берется по всем работам j из множества K(i).
- t(pk,i) = t(rk,i), если работа i не имеет последующих.
- t(pn,i) = t(pk,i) - t(i)t(pk,i) = min t(pn,j), где минимум берется по тем работам j, которые принадлежат множеству K(i), т.е. по тем работам, от которых зависит работа с номером i.
- r(i) = t(pn,i) - t(rn,i) = t(pk,i) - t(rk,i). Работы критического пути — это те работы, резервы времени которых нулевые (r(i) = 0).
Условия
- Граф должен быть без петель и контуров, т.е. антирефлексивным бинарным отношением.
- Вы должны знать конечную работу. Значение времени критического пути смотрится у конечной работы в столбце t(pk, i).
Пример задачи
Итоговая таблица с вычисленными значениями примет вид:
Конечная работа с номером 12. Смотрим у неё значение столбца t(pk, i). Время, за которое гарантированно можно выполнить все работы = 22.
Пишем алгоритм на Python
Начнём с создания модели, которая будет поступать на вход и второй модели, которая будет заполнять нашу таблицу для планирования. Для удобства использую namedtuple (почитать про него можно тут: https://habr.com/ru/articles/438162/):
from collections import namedtuple input_model = namedtuple("input_model", ["time", "set_k"]) row = namedtuple("row", ["i", "time", "set_k", "rn", "rk", "pn", "pk", "r"])Считаем количество работ, которое нужно будет обработать:
По введённым данным начинаем решать задачу сетевого планирования:
- Если у работы нет предшествующих работ (длина множества K(i) = 0), значит это первая работа, с которой начнёт работать наш завод.
- Иначе - определяем максимальное значение раннего окончания зависимых работ.
- Обновляем таблицу.
for number, model in models.items(): time = model.time set_k = model.set_k if len(set_k) == 0: rn = 1 else: rn = max([table[s].rk for s in set_k]) + 1 rk = rn + model.time - 1 table[number] = row(i=number, time=time, set_k=set_k, rn=rn, rk=rk, pn=None, pk=None, r=None) При подсчётах можно увидеть прибавление или убавление единицы. Это дополнительный такт времени, в принципе решать задачу можно без него.
Продолжаем решать задачу сетевого планирования. Проходимся с конца таблицы (последней работы) для подсчётов:
- Ищем все посещённые работы с помощью функции search_next_numbers .
- t(pk, i) - времени самого позднего окончания выполнения работы, считается как минимальное значение выполненных работ.
- t(pn, i) - времени самого позднего начала выполнения работы, считается как t(pk, i) минус время выполнения работы.
- r - резерв времени, считается как t(pn, i) минус t(rn, i).
- В конце можно увидеть assert: проверка на корректность решения задачи (резерв времени должен быть всегда равен времени позднего окончания - времени раннего окончания). Эта строка необязательна, так как использование assert’ов в коде можно отключить и лучше использовать вызовы ошибок с помощью raise Error :).
- Обновляем данные в таблице.
for number, model in list(models.items())[::-1]: visited = search_next_numbers(number) current_row = table[number] if visited: k = min(visited, key=lambda num: table[num].pn if table[num].pn is not None else 10000000000) pk = table[k].pn - 1 else: pk = current_row.rk pn = pk - current_row.time + 1 r = pn - current_row.rn assert r == pk - current_row.rk and r >= 0, print(f", r=, ") table[number] = table[number]._replace(pk=pk, pn=pn, r=r) Для вывода таблицы я использовала библиотеку prettytable. Написала функцию, которая по созданному словарику с табличными данными, будет выводить таблицу:
from prettytable import PrettyTable def print_table(data: dict[int, row]): pretty_table = PrettyTable() pretty_table.field_names = ["i", "t(i)", "K(i)", "t(rn, i)", "t(rk, i)", "t(pn, i)", "t(pk, i)", "r(i)"] for line in data.values(): pretty_set = line.set_k if len(line.set_k) > 0 else "<>" pretty_table.add_row([line.i, line.time, pretty_set, line.rn, line.rk, line.pn, line.pk, line.r]) print(pretty_table) print_table(table) Заключение
Задачи сетевого планирования могут быть использованы в различных сферах деятельности, подразумевающих организацию процессов и контроль за временем выполнения работ. Например, в строительстве они применяются для планирования и управления проектами, определения зависимостей между работами и трудозатрат, а также для контроля за выполнением сроков. В промышленности задачи сетевого планирования используются для оптимизации производственных процессов и расчета затрат времени и ресурсов на производство изделий. В общем, задачи сетевого планирования могут быть полезны для управления любыми проектами, где время является критическим фактором успеха.
Спасибо за просмотр! Делитесь в комментарии своими мыслями по поводу алгоритма и самой задачи сетевого планирования. До встречи в новых статьях.