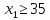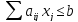- 1. Определение задачи математического программирования
- 2. Допустимое решение задачи, одр, оптимальное решение задачи.
- 3. Экономико–математические модели задач лп: задача о банке
- Задача о банке
- 4. Экономико – математические модели задач лп: задача определения оптимального ассортимента продукции.
- 5. Задача лп, стандартная форма, каноническая форма.
- 2.3. Типы задач математического программирования
- 2.3. Типы задач математического программирования
1. Определение задачи математического программирования
Математическое программирование — это область математики, разрабатывающая теорию, решения многомерных задач с ограничениями. В отличие от классической математики, мы находим наилучший вариант из всех возможных.
Итак, математическое программирование — это раздел высшей математики, занимающийся решением задач, связанных с нахождением экстремумов функций нескольких переменных при наличии ограничений на переменные.
Общая задача М. п. состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений.
Классическая задача математического программирования – задача выбора таких значений некоторых переменных, подчиненных системе ограничений в форме равенств, при которых достигается max или min функции.
2. Допустимое решение задачи, одр, оптимальное решение задачи.
Допустимым решением задачи называется любой n-мерный вектор
x (x = (


Множество допустимых решений образует ОДР.
Оптимальным решением задачи называется такое допустимое решение, при котором целевая функция достигает экстремума.
3. Экономико–математические модели задач лп: задача о банке
К экономико-математическим моделям задач ЛП относятся:Задача планирования производства, определения оптимального ассортимента продукции, о диете, о банке, составления жидких смесей, Транспортная задача
Построение экономико – математической модели.
Задача о банке
Собственные средства банка в сумме с депозитами составляют 100 млн. $. Не менее 35 млн. $ из этой суммы размещена в кредитах (не ликвид). Ликвидное ограничение ценных бумаг должны составлять не менее 30 %, размещенных в кредитах и ликвидных активах.
Пусть 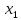

Банк. Огран. (1)
Кред. Огран.
Ликвид. Огран.
Условие неопределенности 



F = при услов. (1) – (4).
4. Экономико – математические модели задач лп: задача определения оптимального ассортимента продукции.


F = 3
2
3
5. Задача лп, стандартная форма, каноническая форма.
К математическим задачам линейного программирования относят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.
Задачей линейного программирования является выбор из множества допустимых планов наиболее выгодного (оптимального).
Экономико-математическая модель любой задачи линейного программирования включает: целевую функцию, оптимальное значение которой (максимум или минимум) требуется отыскать; ограничения в виде системы линейных уравнений или неравенств; требование неотрицательности переменных.
В общем виде модель записывается следующим образом:
Целевая функция: F (x)= c1x1 + c2x2 + . + cnxn → max(min)
ограничения: a11x1 + a12x2 + . + a1nxn b1,
требование неотрицательности: xj ≥ 0,
Задача имеет каноническую форму, если является задачей на максимум (минимум) линейной функции F и ее система ограничений состоит только из равенств (уравнений). При этом переменные задачи х1, х2, . хn являются неотрицательными:
F (x) =
, i= 1,2…m
, j = 1,2…n
В стандартной форме задача линейного программирования является задачей на максимум (минимум) линейной функции f и система ограничений ее состоит из одних линейных неравенств типа «
F (x) =
, i= 1,2…m
, j = 1,2…n
Допустимое множество решений задачи ЛП либо пусто, либо является выпуклым многогранником (как пересечение полупространств, описываемых ограничениями-неравенствами). Оно может быть как ограниченным, так и неограниченным; в любом случае это замкнутый многогранник.
Если допустимое множество не пусто, а целевая функция ограничена сверху (для задачи максимизации, а для задачи минимизации — ограничена снизу) на этом множестве, то задача ЛП имеет оптимальное решение.
Оптимальные решения задачи ЛП (если они существуют) всегда находятся на границе допустимого множества. Точнее, если существует единственное оптимальное решение, то им является какая-либо вершина многогранника допустимых решений; если две или несколько вершин являются оптимальными решениями, то любая их выпуклая комбинация также является оптимальным решением (т.е. существует бесконечно много точек максимума или минимума)
2.3. Типы задач математического программирования
В зависимости от вида функций цели и типа ограничений задачи МП подразделяются на ряд более частных задач: – линейное программирование: функция цели и ограничения являются ли- нейными функциями переменных x i , i = 1, n ; – нелинейное программирование: функция цели и(или) ограничения являются нелинейными; 10
– квадратичное программирование: функция цели квадратичная, а ограничения являются линейными функциями переменных x i , i = 1, n ; – сепарабельное программирование: функция цели и ограничения являются сепарабельными функциями, т.е. представлены в виде сумм n функций, каждая из которых зависит только от одной переменной;
| – геометрическое программирование: функция цели | и ограничения пред- |
| m | n |
| ставлены с помощью положительных полиномов вида å c i Õ x j a ij , где c i – по- | |
| i = 1 | j = 1 |
стоянные положительные коэффициенты, i = 1, m ; a ij – произвольные действи- тельные числа, j = 1, n ; – целочисленное программирование – это задачи, в которых переменные x i могут принимать только целые значения; – стохастическое программирование: коэффициенты в целевой функции или в ограничениях являются случайными величинами. 2.4. Связь между задачей математического программирования и задачей оптимального управления Как уже отмечалось, задача оптимального управления заключается в отыскании такого алгоритма управления u * ( t ) Î U , который переводит ОУ из заданного начального состояния x 0 в конечное x T и обеспечивает экстремум выбранному критерию качества при соблюдении заданных ограничений. Рассмотрим задачу, в которой критерий оптимальности задан функционалом
| T | |
| J = ò F [ x ( t ), u ( t ), t ] dt + G [ x ( T ), T ] , | (2.3) |
| t 0 |
представляющему собой сумму интегральной и терминальной составляющей. Здесь G [ x ( T ), T ] – терминальная функция, она не зависит от управляющего воздействия, а определяется только состоянием объекта в конечный момент времени. При этом должны удовлетворяться уравнения состояния системы
| x & i ( t ) = f i [ x ( t ), u ( t ), t ], i = 1, n | (2.4) |
| и ограничения | |
| g [ x ( t ), t ] £ 0, g [ u ( t ), t ] £ 0 . | (2.5) |
11
Задача оптимального управления фактически является задачей МП [8]. Чтобы
| пояснить это, надо представить | интеграл(2.3) в виде суммы, | разбив | интервал |
| [ t 0 , T ] на N временных подинтервалов: | |||
| T | N | ||
| ò F [ x ( t ), u ( t ), t ] dt = | lim å F [ x ( t k ), u ( t k ), t k ] × ( t k | — t k — 1 ) . | (2.6) |
| t 0 | N ®¥ k = 1 | ||
Уравнения состояния (2.4) при таком разбиении можно представить следующим образом:
| lim | x ( t k ) — x ( t k — 1 ) | = f [ x ( t k ), u ( t k ), t k ] , | (2.7) | |
| ( t k — t k — 1 ) ® 0 | t k — t k — 1 | |||
| а ограничения (2.5) – в виде | ||||
| g [ x ( t k ), t k ] £ 0, g [ u ( t k ), t k ] £ 0 . | (2.8) | |||
| Другими словами, интегрирование заменяется конечным суммированием, а | ||||
| дифференциальные уравнения – | разностными уравнениями. Объединим | (2.6) – | ||
| (2.8), вводя обозначения t k — t k — 1 | = D , x ( t k ) — x ( t k — 1 ) = D x . При этом получим за- | |||
дачу МП:
| ì | N | D x | |
| min(max) m in (m a x ) í lim å F [ x ( t k ), u ( t k ), t k ] × D + G [ x ( t N )] | lim | = | |
| D | |||
| î N ® ¥ k = 1 | D ® 0 | ||
| = f [ x ( t k ), u ( t k ), t k ], | g [ x ( t k ), t k ] £ 0 , g [ u ( t k ), t k ] £ 0 > , | (2.9) | |
в которой неизвестными являются x ( t k ) , u ( t k ) . Число переменных в (2.9) бесконечно, т. е. задача оптимального управления для непрерывной системы образует бесконечномерную задачу МП. При решении практических задач число переменных может быть уменьшено до приемлемой величины. Большая часть работ, посвященных решению задач оптимального управления методами МП, относится к линейным системам. При этом задача оптимального управления сводится к решению задачи линейного программирования (ЛП). 12
2.3. Типы задач математического программирования
В зависимости от вида функций цели и типа ограничений задачи МП подразделяются на ряд более частных задач: – линейное программирование: функция цели и ограничения являются ли- нейными функциями переменных x i , i = 1, n ; – нелинейное программирование: функция цели и(или) ограничения являются нелинейными; 10
– квадратичное программирование: функция цели квадратичная, а ограничения являются линейными функциями переменных x i , i = 1, n ; – сепарабельное программирование: функция цели и ограничения являются сепарабельными функциями, т.е. представлены в виде сумм n функций, каждая из которых зависит только от одной переменной;
| – геометрическое программирование: функция цели | и ограничения пред- |
| m | n |
| ставлены с помощью положительных полиномов вида å c i Õ x j a ij , где c i – по- | |
| i = 1 | j = 1 |
стоянные положительные коэффициенты, i = 1, m ; a ij – произвольные действи- тельные числа, j = 1, n ; – целочисленное программирование – это задачи, в которых переменные x i могут принимать только целые значения; – стохастическое программирование: коэффициенты в целевой функции или в ограничениях являются случайными величинами. 2.4. Связь между задачей математического программирования и задачей оптимального управления Как уже отмечалось, задача оптимального управления заключается в отыскании такого алгоритма управления u * ( t ) Î U , который переводит ОУ из заданного начального состояния x 0 в конечное x T и обеспечивает экстремум выбранному критерию качества при соблюдении заданных ограничений. Рассмотрим задачу, в которой критерий оптимальности задан функционалом
| T | |
| J = ò F [ x ( t ), u ( t ), t ] dt + G [ x ( T ), T ] , | (2.3) |
| t 0 |
представляющему собой сумму интегральной и терминальной составляющей. Здесь G [ x ( T ), T ] – терминальная функция, она не зависит от управляющего воздействия, а определяется только состоянием объекта в конечный момент времени. При этом должны удовлетворяться уравнения состояния системы
| x & i ( t ) = f i [ x ( t ), u ( t ), t ], i = 1, n | (2.4) |
| и ограничения | |
| g [ x ( t ), t ] £ 0, g [ u ( t ), t ] £ 0 . | (2.5) |
11
Задача оптимального управления фактически является задачей МП [8]. Чтобы
| пояснить это, надо представить | интеграл(2.3) в виде суммы, | разбив | интервал |
| [ t 0 , T ] на N временных подинтервалов: | |||
| T | N | ||
| ò F [ x ( t ), u ( t ), t ] dt = | lim å F [ x ( t k ), u ( t k ), t k ] × ( t k | — t k — 1 ) . | (2.6) |
| t 0 | N ®¥ k = 1 | ||
Уравнения состояния (2.4) при таком разбиении можно представить следующим образом:
| lim | x ( t k ) — x ( t k — 1 ) | = f [ x ( t k ), u ( t k ), t k ] , | (2.7) | |
| ( t k — t k — 1 ) ® 0 | t k — t k — 1 | |||
| а ограничения (2.5) – в виде | ||||
| g [ x ( t k ), t k ] £ 0, g [ u ( t k ), t k ] £ 0 . | (2.8) | |||
| Другими словами, интегрирование заменяется конечным суммированием, а | ||||
| дифференциальные уравнения – | разностными уравнениями. Объединим | (2.6) – | ||
| (2.8), вводя обозначения t k — t k — 1 | = D , x ( t k ) — x ( t k — 1 ) = D x . При этом получим за- | |||
дачу МП:
| ì | N | D x | |
| min(max) m in (m a x ) í lim å F [ x ( t k ), u ( t k ), t k ] × D + G [ x ( t N )] | lim | = | |
| D | |||
| î N ® ¥ k = 1 | D ® 0 | ||
| = f [ x ( t k ), u ( t k ), t k ], | g [ x ( t k ), t k ] £ 0 , g [ u ( t k ), t k ] £ 0 > , | (2.9) | |
в которой неизвестными являются x ( t k ) , u ( t k ) . Число переменных в (2.9) бесконечно, т. е. задача оптимального управления для непрерывной системы образует бесконечномерную задачу МП. При решении практических задач число переменных может быть уменьшено до приемлемой величины. Большая часть работ, посвященных решению задач оптимального управления методами МП, относится к линейным системам. При этом задача оптимального управления сводится к решению задачи линейного программирования (ЛП). 12