- 1.3 Примеры постановки задач линейного программирования
- 1.3.1 Пример задачи о диете (о составлении рациона, о смеси)
- 1.6. Примеры экономических задач линейного программирования. Задача о выборе оптимальных технологий
- 1.7. Примеры экономических задач линейного программирования. Задача о смесях
- 1.8. Примеры экономических задач линейного программирования. Транспортная задача
- 1.6. Примеры экономических задач линейного программирования. Задача о выборе оптимальных технологий
- 1.7. Примеры экономических задач линейного программирования. Задача о смесях
- 1.8. Примеры экономических задач линейного программирования. Транспортная задача
1.3 Примеры постановки задач линейного программирования
Задачи линейного программирования, как экономико-математические модели, находят очень широкое применение. Рассмотренная выше задача производственного планирования представляет собой лишь одну из возможных экономических интерпретаций задачи линейного программирования, наиболее традиционную. Множество других экономических ситуаций может быть описано в тех же математических терминах, что делает возможным применение к их решению одного и того же математического аппарата.
Для того чтобы построить математическую модель экономической ситуации в виде задачи линейного программирования, прежде всего необходимо ввести переменные задачи. Они должны быть введены таким образом, чтобы их значения определяли принимаемое решение (получив значения переменных, мы получаем ответ на поставленный вопрос).
Затем определяют цель, критерий эффективности операции, ту величину, которую необходимо экстремизировать в задаче. Ее выражают через введенные переменные — получают линейное выражение для целевой функции.
После этого необходимо установить, чем ограничивается рост или уменьшение целевой функции, т.е. определить ограничения задачи. Их нужно также выразить через переменные и записать в виде системы уравнений и неравенств.
Кроме того, при построении модели полезно воспользоваться следующими рекомендациями. При определении переменных следует заранее обдумать, позволят ли они отразить в модели все условия задачи (если известно, что нет избыточных условий). В конкретной задаче указывают единицы измерения для переменных. Если в исходных данных задачи одна и та же величина измеряется в различных единицах (например, масса в граммах, килограммах, тоннах), то необходимо перевести эти данные в одни и те же единицы измерения. Выражая целевую функцию и ограничения через переменные, следует проверить, какими единицами будут измеряться полученные величины и не являются ли они бессмысленными с экономической точки зрения (например, не измеряются ли левая и правая части ограничений в разных единицах). Отдельно следует обдумать ограничения на знак переменных.
В некоторых задачах переменные могут принимать только целые значения. Этот факт также необходимо записать в виде ограничения: ХZ. Такое ограничение выводит поставленную задачу из класса задач линейного программирования в класс задачцелочисленного линейного программирования. Однако, рассмотренных здесь понятий достаточно для того, чтобы построить математическую модель и для целочисленной задачи.
Приведем некоторые примеры экономических задач, математические модели которых можно построить в виде задач линейного программирования. Следует отметить, что здесь будут рассмотрены далеко не все такие задачи; а кроме того, даже те, что рассмотрены, существуют в разнообразных модификациях, и классификация этих задач в большой мере условна, различается у разных авторов.
1.3.1 Пример задачи о диете (о составлении рациона, о смеси)
Питательная смесь для цыпленка-бройлера состоит из известняка, зерна и соевых бобов, цены на которые соответственно равны 4, 15 и 40 руб. за 1 кг. При этом недельный рацион цыпленка должен содержать не менее 4, но не более 6 г кальция; не менее 110 г белка; не более 25 г клетчатки; каждый цыпленок должен получать ровно 500 г этой смеси. Кальций содержится в известняке в количестве 380 г/кг, в зерне – 1 г/кг и в бобах – 2 г/кг. Белок (и клетчатка) содержатся только в зерне и бобах в количествах соответственно 90 и 50 г/кг (20 и 80 г/кг). Составить смесь минимальной стоимости * .
Построим математическую модель этой ситуации.
В задаче необходимо определить, как составить смесь, т.е. сколько взять каждого ингредиента. Введем переменные: х1– масса известняка, кг; х2– масса зерна, кг; х3– масса бобов, кг.
Цель операции – сделать недельный рацион цыпленка как можно более дешевым. Его стоимость составит 4х1+ 15х2 + 40х3(руб.)
Количество кальция в известняке составит 380х1 г, в зерне х2г, в бобах 2х3г, во всем рационе 380х1 + х2+ 2х3(г), и эта сумма должна быть не менее 4 и не более 6 г: 4380х1 + х2+ 2х36. Белок содержится только в зерне (90х2г) и бобах (50х3г), поэтому 90х2+ 50х3110. Аналогично для клетчатки 20х2+ 80х325.
Кроме того, общая масса этой смеси должна составлять не менее 500 г. Ее масса в килограммах составляет х1+ х2 + х3. Чтобы можно было построить ограничение, необходимо перевести 500 г в килограммы: 500 г = 0,5 кг. Тогда х1+ х2 + х3 = 0,5.
Тогда математическая модель запишется следующим образом:
4380х1 + х2+ 2х36
1.6. Примеры экономических задач линейного программирования. Задача о выборе оптимальных технологий
В задаче о наилучшем использовании ресурсов определяется оптимальный план выпуска продукции. Пусть при производстве какого-то общественно необходимого продукта используется n технологий. При этом требуется m видов ресурсов, заданных объемами 






,
при ограничениях на лимитируемые ресурсы
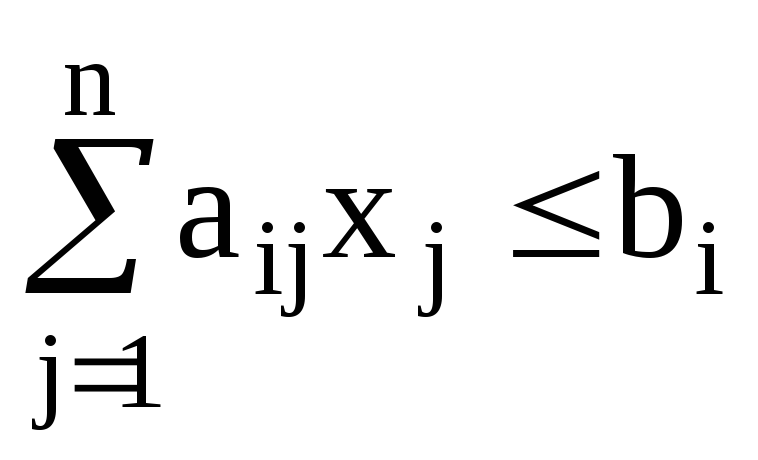

и условия неотрицательности


1.7. Примеры экономических задач линейного программирования. Задача о смесях
В различных отраслях народного хозяйства возникает проблема составления таких рабочих смесей на основе исходным материалов, которые обеспечивали бы получение конечного продукта, обладающего определенными свойствами. К этой группе относят задачи о выборе диеты, составления кормового рациона в животноводстве, шихт в металлургии, горючих и смазочных смесей в нефтеперерабатывающей промышленности и т.д. Высокий уровень затрат на исходные сырьевые материалы и необходимость повышения эффективности производства выдвигает на первый план следующую задачу: получить продукцию с заданными свойствами при наименьших затратах на исходные сырьевые материалы.
Модель задачи о наилучшем составе смеси рассмотрим на примере задачи о диете. Имеются пищевые продукты, известные под номерами 1, 2, 3, . j, . n. Они содержат различные питательные вещества, обозначаемые номерами 1, 2, 3, . i, . m (углеводы, белки, жиры, витамины, микроэлементы и др.). Единица j-го продукта содержит 



Математическая модель задачи:
,




1.8. Примеры экономических задач линейного программирования. Транспортная задача
Рассмотрим простейший вариант модели транспортной задачи, когда речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителям, при этом имеется баланс между суммарным спросом потребителей и возможностями поставщиков по их удовлетворению. Причем, потребителям безразлично, из каких пунктов производства будет поступать продукция, лишь бы их заявки были полностью удовлетворены. От схемы прикрепления потребителей к поставщикам существенно зависит объем транспортной работы, возникает задача о наиболее рациональном прикреплении, правильном направлении перевозок грузов, при котором потребности полностью удовлетворяются, вся продукция от поставщиков вывозится, а затраты на транспортировку минимальны.
Задача формулируется так: имеется m пунктов производства, в каждом из которых сосредоточено 



.
Известны величины 
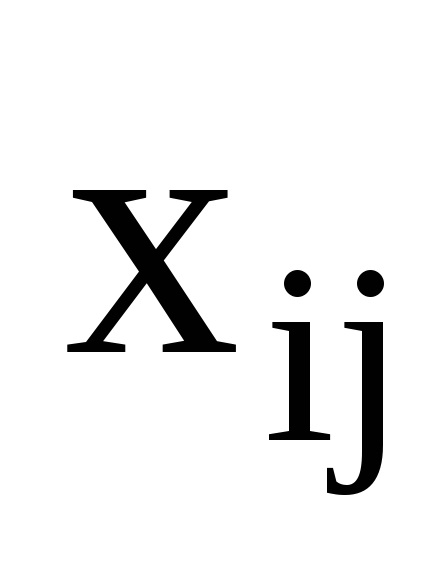

Матрица Х=|||| — матрицей перевозок:
С целью удобства построения математической модели матрицы тарифов и перевозок совмещают в одну, именуемую макетом транспортной задачи:
1.6. Примеры экономических задач линейного программирования. Задача о выборе оптимальных технологий
В задаче о наилучшем использовании ресурсов определяется оптимальный план выпуска продукции. Пусть при производстве какого-то общественно необходимого продукта используется n технологий. При этом требуется m видов ресурсов, заданных объемами 
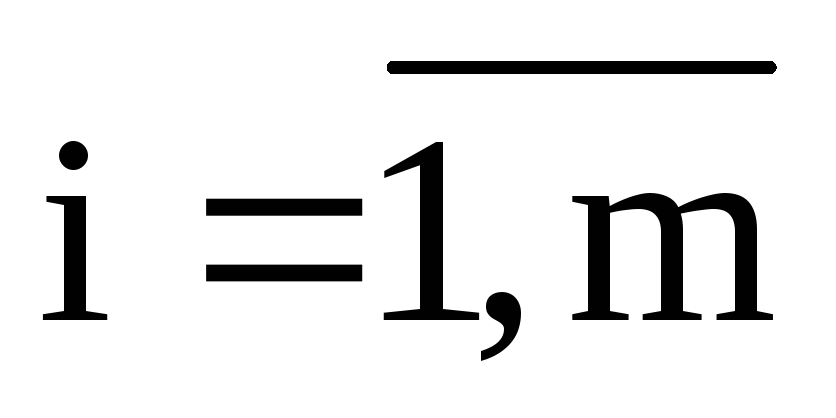




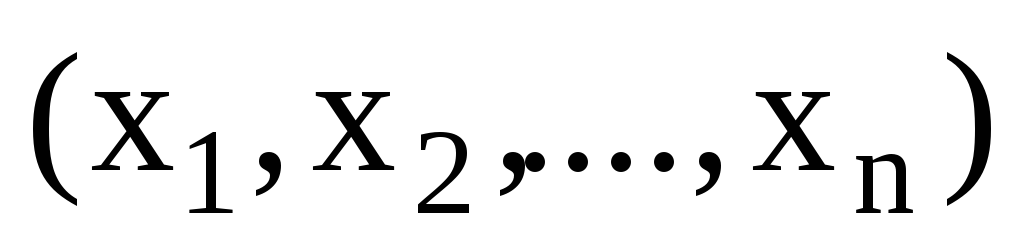
,
при ограничениях на лимитируемые ресурсы
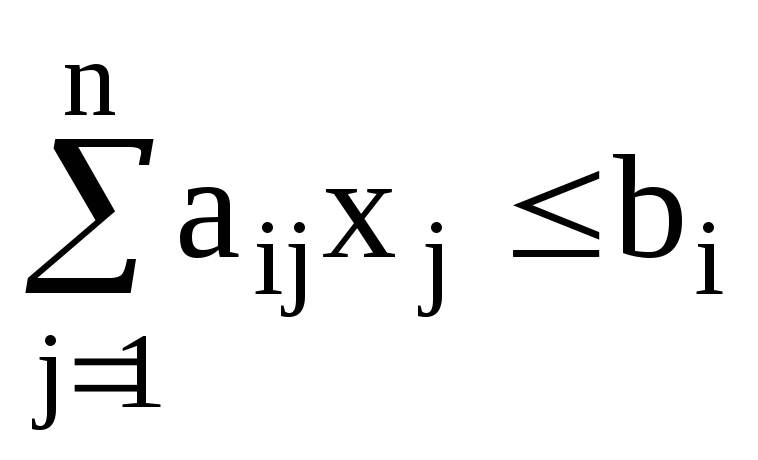
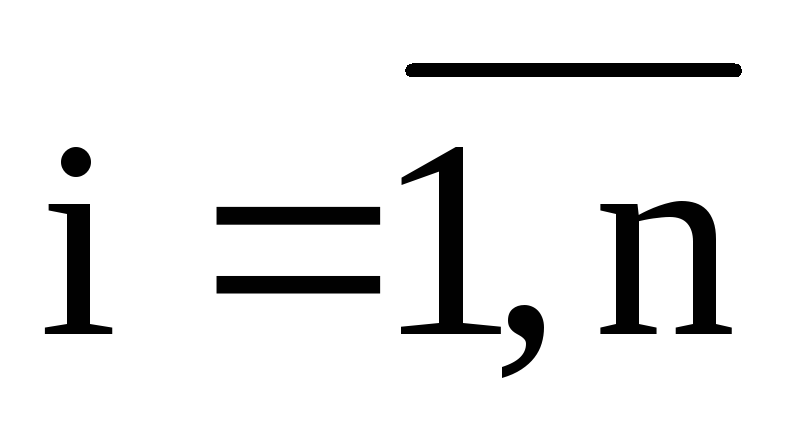
и условия неотрицательности


1.7. Примеры экономических задач линейного программирования. Задача о смесях
В различных отраслях народного хозяйства возникает проблема составления таких рабочих смесей на основе исходным материалов, которые обеспечивали бы получение конечного продукта, обладающего определенными свойствами. К этой группе относят задачи о выборе диеты, составления кормового рациона в животноводстве, шихт в металлургии, горючих и смазочных смесей в нефтеперерабатывающей промышленности и т.д. Высокий уровень затрат на исходные сырьевые материалы и необходимость повышения эффективности производства выдвигает на первый план следующую задачу: получить продукцию с заданными свойствами при наименьших затратах на исходные сырьевые материалы.
Модель задачи о наилучшем составе смеси рассмотрим на примере задачи о диете. Имеются пищевые продукты, известные под номерами 1, 2, 3, . j, . n. Они содержат различные питательные вещества, обозначаемые номерами 1, 2, 3, . i, . m (углеводы, белки, жиры, витамины, микроэлементы и др.). Единица j-го продукта содержит 



Математическая модель задачи:
,




1.8. Примеры экономических задач линейного программирования. Транспортная задача
Рассмотрим простейший вариант модели транспортной задачи, когда речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителям, при этом имеется баланс между суммарным спросом потребителей и возможностями поставщиков по их удовлетворению. Причем, потребителям безразлично, из каких пунктов производства будет поступать продукция, лишь бы их заявки были полностью удовлетворены. От схемы прикрепления потребителей к поставщикам существенно зависит объем транспортной работы, возникает задача о наиболее рациональном прикреплении, правильном направлении перевозок грузов, при котором потребности полностью удовлетворяются, вся продукция от поставщиков вывозится, а затраты на транспортировку минимальны.
Задача формулируется так: имеется m пунктов производства, в каждом из которых сосредоточено 



.
Известны величины 


Матрица Х=|||| — матрицей перевозок:
С целью удобства построения математической модели матрицы тарифов и перевозок совмещают в одну, именуемую макетом транспортной задачи:












