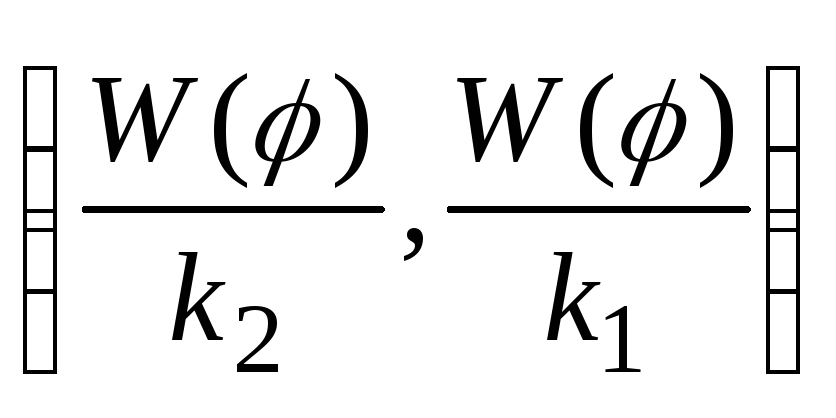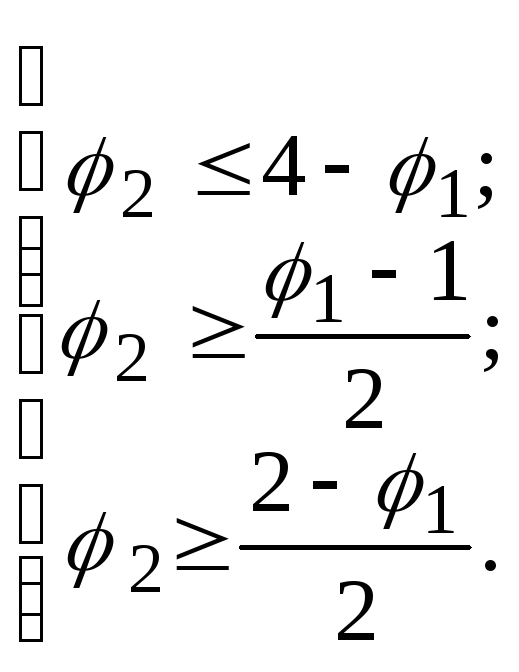Глава 4. Задачи линейного программирования
4.1. Основные понятия о задачах линейного программирования
Линейное программирование относится к числу наиболее часто используемых методов оптимизации. Это наиболее эффективный способ решения задачи оптимизации в тех случаях, когда целевая функция может быть представлена линейной формой, а балансовые уравнения – системой линейных алгебраических уравнений. Решение систем линейных уравнений намного проще, чем решение систем нелинейных уравнений. Методы решения систем линейных уравнений появились намного раньше и в настоящее время легко программируемы. Данные достоинства линейной формы, а также наличие алгоритмов, реализующих этот метод оптимизации, являются причинами его эффективности, особенно на этапах предварительного выбора [1].
Первые исследования по линейному программированию были проведены в 30-е годы в Ленинградском университете академиком Л. В. Канторовичем. Термин «линейное программирование» появился в 1951 году в работах американских ученых Дж. Б. Данцига и Т. Купманса, еще до появления общепринятого сейчас понятия «программирование». Благодаря данному обстоятельству оптимизационные методы нахождения решения, обращающего в максимум (минимум) целевую функцию W() при существовании балансовых ограничений в виде равенств иди неравенств, получили название методов математического программирования [12].
Следует отметить, что математическое программирование представляет собой не аналитическую, а алгоритмическую форму решения задачи, т. е. дает не формулу, выражающую окончательный результат, а указывает лишь вычислительную процедуру, которая приводит к решению задачи. Поэтому методы математического программирования становятся эффективными главным образом при использовании ЭВМ, особенно в тех случаях, когда размерность задачи не позволяет вручную найти ее решение [7].
Постановка задачи линейного программирования
В задаче линейного программирования целевая функция W() (иначе говоря, интегральный критерий или показатель эффективности) линейно зависит от своих аргументов (оценок альтернатив по критериям) i, а ограничения gj() имеют вид линейных равенств или неравенств.
Задача поставлена, как задача линейного программирования, если:
Требуется найти максимум или минимум целевой функции
W() = ,
при ограничениях
где i – оценки альтернатив по i–му критерию;
gj() – функция, показывающая j–е ограничение на оценки альтернатив по критериям ;
ci – линейный коэффициент, показывающий «вклад» i–го критерия в интегральный W();
aij – линейный коэффициент, показывающий «силу» ограничения на i–й критерий в gj();
bj – константа, показывающая отличие gj() от 0 –ограничение на j–й ресурс.
Приведем несколько различных постановок задач линейного программирования [2].
1. Задача о пищевом рационе.
Из четырех продуктов питания Пi (i =1, 2, 3, 4) составить суточный пищевой рацион с минимальной стоимостью, но обеспечивающий необходимое количество питательных элементов: белков, углеводов и жиров.
При этом известно, что стоимость единицы i–го продукта питания составляет ci, причем одна единица i–го продукта питания содержит количество белков – ai1 , количество углеводов – ai2 , количество жиров – ai3, а суточный пищевой рацион должен включать не менее b1 единиц белков, не менее b2 единиц – углеводов и не менее b3 единиц – жиров.
Сведем все исходные данные в таблицу:
Задача заключается в том, чтобы найти такие значения единиц продуктов питания в суточном пищевом рационе 1, 2, 3, 4, при которых значение целевой функции W() – стоимость суточного пищевого рациона обращается в минимум.
Выведем формулу для целевой функции, которую необходимо минимизировать:
,
при ограничениях
Последние четыре ограничения связаны с тем, что в суточный рацион не может быть включено отрицательное количество единиц продукта питания.
2. Задача о распределении ресурсов.
Имеется m ресурсов в количестве b1, b2, …, bm единиц. С их помощью можно производить Т1, Т2, …, Тn единиц товаров n видов. Для производства одной единицы Тi товара i–го вида необходимо aij единиц j–го ресурса. Одна единица j–го ресурса стоит dj рублей. Каждая единица товара i–го вида может быть реализована по цене ci рублей. Рынок не может поглотить больше, чем ki единиц товара i–го вида.
Какое количество единиц товара каждого вида нужно производить, чтобы получить максимальную прибыль?
Введем n переменных qi = ci – si – чистая прибыль от производства и реализации одной единицы товара i–го вида, где si = –себестоимость одной единицы товара i–го вида, которая равна суммарной стоимости всех ресурсов, затрачиваемых на производство одной единицы товара i–го вида.
Задача заключается в том, чтобы найти такие количества единиц товара каждого из n видов 1, 2, …, n, которые целесообразно производить, для того чтобы значение целевой функции W() – прибыль от производства и реализации товаров обращалась в максимум.
Тогда можно сформулировать целевую функцию, которую необходимо максимизировать:
,
при ограничениях
Первая группа ограничений связана с тем, что всех ресурсов должно хватить на производство товаров всех типов. Вторая группа ограничений связана с тем, что не нужно производить товара i–го вида больше, чем нужно на рынке. Последняя группа ограничений говорит о том, что нельзя произвести отрицательное количество товара.
3. Еще одна задача о распределении ресурсов.
Вычислительным комплексом, состоящим из m средств обработки, необходимо решить n задач (n m). При этом каждая i-я задача требует tij времени для ее выполнения в j-м средстве и aij — емкостных ресурсов для ее размещения (временного хранения) в j-м средстве. Каждое j–е средство имеет емкость (объем) памяти bj. Каждая задача решается только в одном из средств обработки от начала до конца, т.е. не может решаться в нескольких средствах обработки по частям. Каждое средство обработки ограничено по количеству решаемых задач только емкостью своей памяти. Необходимо так распределить задачи между средствами обработки, чтобы суммарное время выполнения n задач было минимальным.
Задача заключается в том, чтобы определить какое средство на какую задачу назначить, чтобы суммарное время выполненияn задач было минимальным. Для этого введем переменные
Тогда можно сформулировать целевую функцию, которую необходимо минимизировать
,
при ограничениях
Первая группа ограничений показывает, что нельзя распределить средство на решение задачи, если его ресурс по емкости памяти уже исчерпан (память занята). Вторая группа ограничений определяет, что каждая i-я задача решается только в одном из средств обработки. А третья группа ограничений говорит о том, что средство не может выполнять отрицательное количество задач.
Последняя задача о распределении ресурсов очень похожа по формулировке на транспортную задачу линейного программирования. И действительно, многие задачи о распределении ресурсов решаются методами решения транспортных задач. К таким задачам относится, например, задача выработки оптимального плана распределения ЗОС на опасные воздушные цели.
4. Транспортная задача.
Имеется n складов и m пунктов потребления. На складах имеются запасы однотипного товара a1, …, an. Пункты потребления подали заявки на количество товара b1, …, bm. Сумма заявок не превосходит суммы запасов (т. е. все заявки могут и должны быть выполнены). Стоимость перевозки единицы товара соi-го склада в j-й пункт равна cij.
Составить такой план перевозок, чтобы все заявки были выполнены, а общие расходы на перевозки были минимальными. Т. е. определить с какого склада и сколько единиц товара выгоднее перевезти в каждый из пунктов потребления.
Задача заключается в том, чтобы определить с какого склада в какой пункт и сколько единиц товара следует перевезти, чтобы суммарная стоимость всех перевозок была минимальной при условиях, что со склада нельзя вывести товара больше, чем имеется на складе, и что все заявки пунктов потребления будут выполнены.
Тогда можно сформулировать целевую функцию, которую необходимо минимизировать
при ограничениях 

где первая группа ограничений показывает, что со склада нельзя вывести товара больше, чем на нем имеется, а вторая – что все заявки пунктов потребления должны быть выполнены.
Хотя постановки разных задач линейного программирования различны, все задачи линейного программирования имеют общие черты: требуется найти такие неотрицательные значения переменных, чтобы
- выполнялись некоторые ограничения, имеющие вид линейных неравенств или равенств относительно этих переменных;
- некоторая линейнаяцелевая функция(показатель эффективности)W() тех же переменныхобращалась в максимум или минимум.
После изучения методов решения задач нелинейного программирования может возникнуть вопрос: «Нельзя ли решать задачи линейного программирования, продифференцировав целевую функцию по всем переменным и приравняв производные нулю решить полученную систему уравнений?» Оказывается, НЕЛЬЗЯ! Т. к. целевая функция линейна, то производные по всем аргументам в ноль не обращаются. Максимум или минимум целевой функции, если он существует, достигается всегда где-то на границе области возможных значений 1, …, n, т. е. там, где начинают действовать ограничения. Следовательно, для решения задач линейного программирования нужен специальный математический аппарат. Графический способ решения задач линейного программирования Самым простым и наиболее наглядным способом решения задач ЛП является графический способ [12]. К сожалению, он применим только когда количество критериев i не велико, например, равно двум. Рассмотрим применение данного способа на примере: Пусть нужно найти максимум целевой функции