Задачи линейного программирования номера

Симплексный метод решения ЗЛП

Симплекс-метод — это итеративный процесс направленного решения системы уравнений по шагам, который начинается с опорного решения и в поисках лучшего варианта движется по угловым точкам области допустимого решения, улучшающих значение целевой функции до тех пор, пока целевая функция не достигнет оптимального значения.

• в виде симплексной таблицы (метод жордановых преобразований); базовой форме записи;
• модифицированным симплекс-методом; в столбцовой форме; в строчечной форме.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word
• Также решают

Инструкция . Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word и Excel . При этом ограничения типа x_i≥0 не учитывайте. Если в задании для некоторых x_i отсутствуют ограничения, то ЗЛП необходимо привести к КЗЛП, или воспользоваться этим сервисом. При решении автоматически определяется использование М-метода (симплекс-метод с искусственным базисом) и двухэтапного симплекс-метода.

Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.

Задачи динамического программирования
Распределить 5 однородных партий товара между тремя рынками так, чтобы получить максимальный доход от их продажи. Доход от продажи на каждом рынке G(X) зависит от количества реализованных партий товара Х и представлен в таблице.

Объем товара Х (в партиях)	Доход G(X)
	1	2	3
0	0	0	0
1	28	30	32
2	41	42	45
3	50	55	48
4	62	64	60
5	76	76	72

1. Составление первого опорного плана. Переход к канонической форме задачи линейного программирования путем введения неотрицательных дополнительных балансовых переменных.
2. Проверка плана на оптимальность. Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план не оптимальный, и его необходимо улучшить.
3. Определение ведущих столбца и строки. Из отрицательных коэффициентов индексной строки выбирается наибольший по абсолютной величине. Затем элементы столбца свободных членов симплексной таблицы делит на элементы того же знака ведущего столбца.
4. Построение нового опорного плана. Переход к новому плану осуществляется в результате пересчета симплексной таблицы методом Жордана—Гаусса.

Аналитическое введение в симплекс-метод

Симплексный метод является универсальным методом линейного программирования. Итак, если мы решаем ЗЛП в канонической форме, то система ограничений — это обычная система линейных уравнений. При решении задач ЛП получаются системы линейных уравнений, имеющие, как правило, бесконечно много решений. Например, пусть дана система
Здесь число уравнений равно 2, а неизвестных — 3, уравнений меньше. Выразим x₁ и x₂ через x₃ :
Это общее решение системы. если переменной x₃ придавать произвольные числовые значения, то будем находить частные решения системы. Например, x₃=1 → x₁=1 → x₂=6. Имеем (1, 6, 1) — частное решение. Пусть x₃=2 → x₁=-3, x₂= 1, (-3, 1, 2) — другое частное решение. Таких частных решений бесконечно много. Переменные x₁ и x₂ называются базисными, а переменная x₃ — не базисная, свободная. Совокупность переменных x₁ и x₂ образует базис: Б (x₁, x₂). Если x₃ = 0, то полученное частное решение (5, 11, 0) называется базисным решением, соответствующим базису Б (x₁, x₂). Базисным называется решение, соответствующее нулевым значениям свободных переменных.
В качестве базисных можно было взять и другие переменные: (x₁, x₃) или (x₂, x₃).
Как переходить от одного базиса Б(x₁, x₂) к другому базису Б(x₁, x₃)?
Для этого надо переменную x₃ перевести в базисные, а x₂ — в небазисные т. е. в уравнениях надо x₃ выразить через x₂ и подставить в 1-е: Базисное решение, соответствующее базису Б (x₁, x₃), таково: (-19/5; 0; 11/5). Если теперь от базиса Б (x₁, x₃) нам захочется перейти к базису Б (x₂, x₃), то
Базисное решение, соответствующее базису Б (x₂, x₃): (0;19/4; 7/8).
Из трех найденных базисных решений решение, соответствующее базису Б (x₁, x₃) — отрицательное x₁ < 0, нас в ЗЛП интересуют только неотрицательные решения. Если задача ЛП имеет решение, то оно достигается на множестве базисных неотрицательных решений системы ограничений канонической формы. Поэтому идея симплекс-метода и состоит в последовательном переходе от одного базиса к другому, лучшему с точки зрения значения целевой функции. Пример . Решить задачу ЛП. Функцию F= x₂ — x₁ → min необходимо минимизировать при заданной системе ограничений:
-2x₁ + x₂ + x₃ = 2
x₁ + x₂ + x₅ = 5
x₁ — 2x₂ + x₄ = 12
x_i ≥ 0, i = 1, 5 Эти ограничения могут рассматриваться как произошедшие из неравенств, а переменные x₃, x₅, x₄ — как дополнительные.
Запишем ограничения, выбрав базис из переменных Б< x₃, , x₄, x₅>: Этому базису соответствует базисное неотрицательное решение
x₁ = 0, x₂ = 0, x₃ = 2, x₄ = 2, x₅ = 5 или (0, 0, 2, 2, 5).
Теперь нужно выразить F через небазисные переменные, в нашем случае это уже сделано: F= x₂ — x₁.
Проверим, достигла ли функция F своего минимального значения. Для этого базисного решения F= 0 — 0 = 0 — значение функции равно 0. Но его можно уменьшить, если x₁ будет возрастать, т. к. коэффициент в функции при x₁ отрицателен. Однако при увеличении x₁ значения переменных x₄, x₅ уменьшаются (смотрите второе и третье равенство системы ограничений). Переменная x₁ не может быть увеличена больше чем до 2, иначе x₄ станет отрицательной (ввиду равенства 2), и не больше, чем до 5, иначе x₅ — отрицателен. Итак, из анализа равенств следует, что переменную x₁ можно увеличить до 2, при этом значение функции уменьшится.
Перейдем к новому базису Б₂, введя переменную x₁ в базис вместо x₄.
Б₂x₁, x₃, x₅>.
Выразим эти базисные переменные через небазисные. Для этого сначала выразим x₁ из второго уравнения и подставим в остальные, в том числе и в функцию. Имеем:

F = -2 — x₂ + x₄.
Базисное решение, соответствующее базису Б₂x₁, x₃, x₅>, имеет вид (2, 0, 6, 0, 3), и функция принимает значение F= -2 в этом базисе.
Значение функции можно и дальше уменьшать, увеличивая x₂. Однако, глядя на систему, x₂ можно увеличивать лишь до 1, т. к. иначе из последнего равенства x₅ = 3 — 3x₂ + x₄ следует, что при x₂ > 1 x₅ станет отрицательной. А у нас все переменные в ЗЛП предполагаются неотрицательными. Остальные уравнения системы не дают ограничений на x₂. Поэтому увеличим x₂ до 1, введя его в базис вместо x₅: Б₃x₁, x₂, x₃>.
Выразим x₂ через x₅ и подставим во все уравнения:

Базисное решение, соответствующее базису Б₃х₁, х₂, х₃>, выписывается (4, 1, 9, 0, 0), и функция принимает значение F= -3. Заметим, что значение F уменьшилось, т. е. улучшилось по сравнению с предыдущим базисом.
Посмотрев на вид целевой функции , заметим, что улучшить, т. е. уменьшить значение F нельзя и только при x₄ = 0, x₅ = 0 значение F= -3. как только x₄, x₅ станут положительными, значение F только увеличится, т. к. коэффициенты при x₄, x₅ положительны. Значит, функция F достигла своего оптимального значения F* = -3. Итак, наименьшее значение F, равное -3, достигается при x₁* = 4, x₂* = 1, x₃* = 9, x₄* = 0, x₅* = 0. На этом примере очень наглядно продемонстрирована идея метода: постепенно переходя от базиса к базису, при этом всегда обращая внимание на значения целевой функции, которые должны улучшиться, мы приходим к такому базису, в котором значение целевой функции улучшить нельзя, оно оптимально. Заметим, что базисов конечное число, поэтому количество шагов, совершаемых нами до того нужного базиса, конечно.

Источник

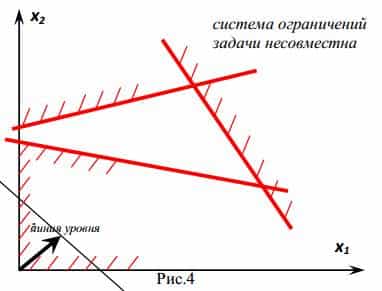
Графический метод решения ЗЛП

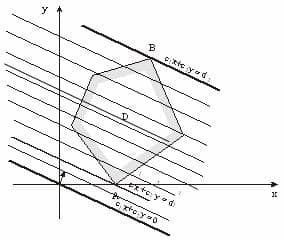
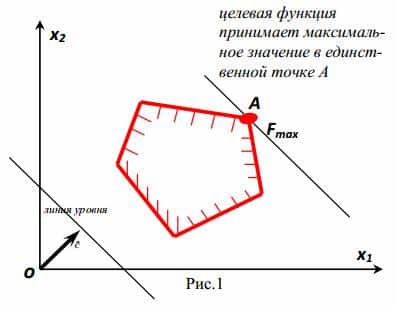
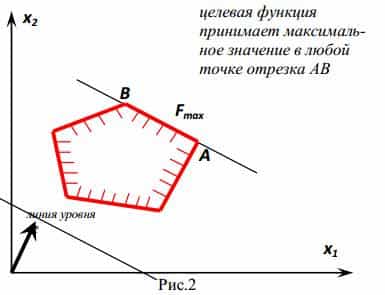
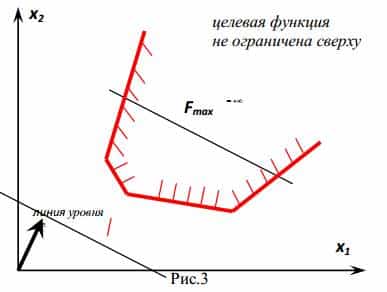
В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений (см. рисунок).

Инструкция . Выберите количество строк (количество ограничений). Если количество переменных больше двух, необходимо систему привести к СЗЛП (см. пример и пример №2). Если ограничение двойное, например, 1 ≤ x₁ ≤ 4 , то оно разбивается на два: x₁ ≥ 1 , x₁ ≤ 4 (т.е. количество строк увеличивается на 1).
Построить область допустимого решения (ОДР) можно также с помощью этого сервиса.

Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.

1. На плоскости X₁0X₂ строят прямые.
2. Определяются полуплоскости.
3. Определяют многоугольник решений;
4. Строят вектор N(c₁,c₂), который указывает направление целевой функции;
5. Передвигают прямую целевую функцию c₁x₂ + c₂x₂ = 0 в направлении вектора N до крайней точки многоугольника решений.
6. Вычисляют координаты точки и значение целевой функции в этой точке.

Целевая функция принимает экстремальное (минимальное или максимальное) значение в единственной точке А.

1. Сформулировать математическую модель задачи линейного программирования.
2. Решить задачу линейного программирования графическим способом (для двух переменных).

Если количество переменных в задаче линейного программирования больше двух, то задачу предварительно сводят к стандартной ЗЛП.
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅ → max при ограничениях:
x₁ + x₂ + x₃=12
2x₁ — x₂ + x₄=8
— 2x₁ + 2x₂ + x₅=10
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:

1	1	1	0	0	12
2	-1	0	1	0	8
-2	2	0	0	1	10

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₃.
2. В качестве базовой переменной можно выбрать x₄.
3. В качестве базовой переменной можно выбрать x₅.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x₁ + x₂ + x₃ = 12
2x₁ — x₂ + x₄ = 8
— 2x₁ + 2x₂ + x₅ = 10
Выразим базисные переменные через остальные:
x₃ = — x₁ — x₂+12
x₄ = — 2x₁ + x₂+8
x₅ = 2x₁ — 2x₂+10
Подставим их в целевую функцию:
F(X) = 3x₁ — 2x₂ + 5(- x₁ — x₂+12) — 4(2x₁ — 2x₂+10)
или
F(X) = — 10x₁ + x₂+20 → max
Система неравенств:
— x₁ — x₂+12 ≥ 0
— 2x₁ + x₂+8 ≥ 0
2x₁ — 2x₂+10 ≥ 0
Приводим систему неравенств к следующему виду:
x₁ + x₂ ≤ 12
2x₁ — x₂ ≤ 8
— 2x₁ + 2x₂ ≤ 10
F(X) = — 10x₁ + x₂+20 → max

Особенности решения задач линейного программирования графическим методом

Переменную x₂ принимаем в качестве дополнительной переменной и делаем замену на знак «≥»:
f=x₁ + 6x₃+ 27
x₁ + 3x₃≥6

Далее задача решается графическом способом.

Пример №2
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅ → max при ограничениях:
x₁ + x₂ + x₃=12
2x₁ — x₂ + x₄=8
— 2x₁ + 2x₂ + x₅=10
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:

1	1	1	0	0	12
2	-1	0	1	0	8
-2	2	0	0	1	10

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₃.
2. В качестве базовой переменной можно выбрать x₄.
3. В качестве базовой переменной можно выбрать x₅.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x₁ + x₂ + x₃ = 12
2x₁ — x₂ + x₄ = 8
— 2x₁ + 2x₂ + x₅ = 10
Выразим базисные переменные через остальные:
x₃ = — x₁ — x₂+12
x₄ = — 2x₁ + x₂+8
x₅ = 2x₁ — 2x₂+10
Подставим их в целевую функцию:
F(X) = 3x₁ — 2x₂ + 5(- x₁ — x₂+12) — 4(2x₁ — 2x₂+10)
или
F(X) = — 10x₁ + x₂+20 → max
Система неравенств:
— x₁ — x₂+12 ≥ 0
— 2x₁ + x₂+8 ≥ 0
2x₁ — 2x₂+10 ≥ 0
Приводим систему неравенств к следующему виду:
x₁ + x₂ ≤ 12
2x₁ — x₂ ≤ 8
— 2x₁ + 2x₂ ≤ 10
F(X) = — 10x₁ + x₂+20 → max

• Составить систему математических зависимостей (неравенств) и целевую функцию.
• Изобразить геометрическую интерпретацию задачи.
• Найти оптимальное решение.
• Провести аналитическую проверку.
• Определить существенные и несущественные ресурсы и их избытки.
• Определить значение целевой функции.
• Вычислить объективно обусловленные оценки.
• Составить соотношение устойчивости.

Источник