Задачи линейного программирования может быть решена методом крамера

1.2 Методы решения задач линейного программирования

Математическое моделирование в исследовании операций является, с одной стороны, очень важным и сложным, а с другой — практически не поддающимся научной формализации процессом. Заметим, что неоднократно предпринимавшиеся попытки выделить общие принципы создания математических моделей приводили либо к декларированию рекомендаций самого общего характера, трудно приложимых для решения конкретных проблем, либо, наоборот, к появлению рецептов, применимых в действительности только к узкому кругу задач. Поэтому более полезным представляется знакомство с техникой математического моделирования на конкретных примерах. [3]

Задачи линейного программирования можно решить следующими методами:

• алгоритмом Флойда;
• алгоритм Дейкстры на графах;
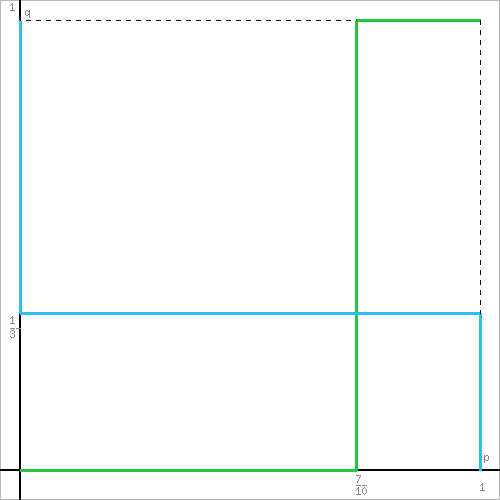
• графический метод;
• метод симплекс-таблиц и др.

Алгоритм решения задач линейного программирования методом Дейкстры на графах. В простейшей реализации для хранения чисел d[i] можно использовать массив чисел, а для хранения принадлежности элемента множеству U — массив булевых переменных. В начале алгоритма расстояние для начальной вершины полагается равным нулю, а все остальные расстояния заполняются большим положительным числом (большим максимального возможного пути в графе). Массив флагов заполняется нулями. Затем запускается основной цикл. На каждом шаге цикла необходимо найти вершину U с минимальным расстоянием и флагом равным нулю. Затем нужно установить в ней флаг в 1 и проверяем все соседние с ней вершины U. Если расстояние больше, чем сумма расстояния до текущей вершины и длины ребра, то необходимо уменьшить его. Цикл завершается, когда флаги всех вершин становятся равны 1, либо когда у всех вершин c флагом 0. Последний случай возможен тогда и только тогда, когда граф G не связан. [4] Способом решения задач линейного программирования графическим методом. Графический метод решения задачи линейного программирования основан на геометрической интерпретации задачилинейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задачтрёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно. Пусть задача линейного программирования задана в двумерном пространстве, то есть ограничения содержат две переменные. Минимальное значение функции определено формулой (1). (1) Ограничения представлены формулами (2) и (3). (2) и (3) Пусть система (2) при условии (3) совместна. Каждое из неравенств из систем (2) и (3) определяет полуплоскость с граничными прямыми представлено формулой(4): (4) Линейная функция (1) при фиксированных значениях Z является уравнением прямой линии: Необходимо построить многоугольник решений системыограничений (2) и графиклинейной функции(1) при Z=0. Тогда поставленной задаче линейного программирования можно дать следующую интерпретацию: Найти точку многоугольника решений, в которой прямая опорная и функция Z при этом достигает минимума. Значения уменьшаются в направлениивектора , поэтому прямую Z=0 необходимо передвигать параллельно самой себе в направлении вектора N. Если многоугольникрешений ограничен, то прямая дважды становится опорной по отношению к многоугольнику решений (в точкахB и E), причём минимальное значение принимает в точке E. Координаты точки необходимо найти, решая систему уравнений прямых DE и EF. Если же многоугольник решений представляет собой неограниченную многоугольную область, то возможны два случая. Случай 1. Прямая , передвигаясь в направлении вектораN или противоположно ему, постоянно пересекает многоугольник решений и ни в какой точке не является опорной к нему. В этом случае линейная функцияне ограничена на многоугольнике решений как сверху, так и снизу. Случай 2. Прямая, передвигаясь, всё же становится опорной относительно многоугольника решений. Тогда в зависимости от вида области линейная функция может быть ограниченной сверху и неограниченной снизу, ограниченной снизу и неограниченной сверху, либо ограниченной как снизу, так и сверху.[5] Для решения данной задачи был выбран наиболее известный и широко применяемый на практике для решения задач линейного программирования является симплекс-метод. Несмотря на то, что симплекс-метод является достаточно эффективным алгоритмом, показавшим хорошие результаты при решении прикладных задач линейного программирования, он является алгоритмом сэкспоненциальной сложностью. Симплексный метод задач линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает или убывает. [6] Перед составлением симплекс-таблицы задача должна быть преобразована, система ограничений приведена к допустимому базисному виду, c помощью которого из целевой функции должны быть исключены базисные переменные как показано на рисунке 1. Рисунок 1 – Начальное преобразование системы ограничений Здесь для определенности записи считается, что в качестве базисных переменных можно взять переменные X1, X2, . Xr и что при этом b1, b2. br ≥ 0 (соответствующее базисное решение является опорным). Для составления симплекс-таблицы во всех равенствах в условии задачи члены, содержащие переменные, переносятся в левую часть, свободные оставляются справа, т.е. задача записывается в виде системы равенствкак показано на рисунке 2. Рисунок 2 – Преобразование системы неравенств Далее эта система оформляется в виде симплекс-таблиц. Алгоритм перехода к следующей таблице такой:

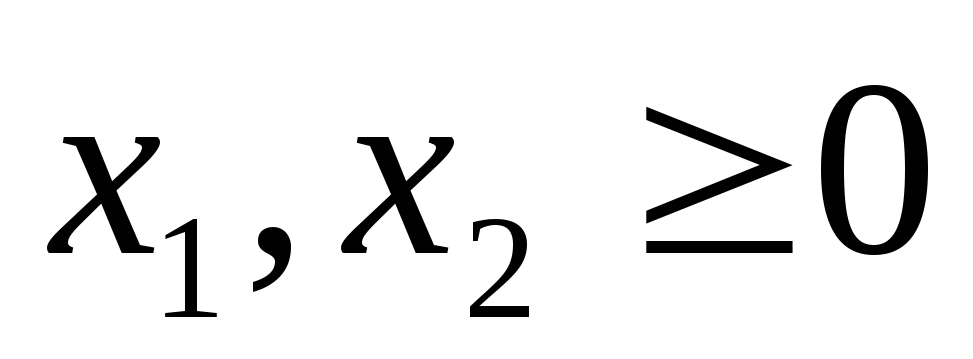
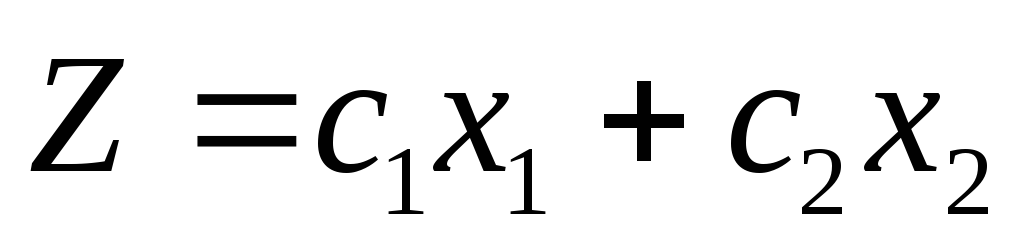
• просматривается последняя строка (индексная) таблицы и среди коэффициентов этой строки (исключая столбец свободных членов ) выбирается наименьшее отрицательное число при отыскании max, либо наибольшее положительное при задачи на min. Если такового нет, то исходное базисное решение является оптимальным и данная таблица является последней;
• просматривается столбец таблицы, отвечающий выбранному отрицательному (положительному) коэффициенту в последней строке- ключевой столбец, и в этом столбце выбираются положительные коэффициенты. Если таковых нет, то целевая функция неограниченна на области допустимых значений переменных и задача решений не имеет;
• среди выбранных коэффициентов столбца выбирается тот, для которого абсолютная величина отношения соответствующего свободного члена (находящегося в столбце свободных членов) к этому элементу минимальна. Этот коэффициент называется разрешающим, а строка в которой он находится ключевой;
• в дальнейшем базисная переменная, отвечающая строке разрешающего элемента, должна быть переведена в разряд свободных, а свободная переменная, отвечающая столбцу разрешающего элемента, вводится в число базисных. Строится новая таблица, содержащая новые названия базисных переменных:
• разделим каждый элемент ключевой строки (исключая столбец свободных членов) на разрешающий элемент и полученные значения запишем в строку с измененной базисной переменной новой симплекс таблицы.
• строка разрешающего элемента делится на этот элемент и полученная строка записывается в новую таблицу на то же место.
• в новой таблице все элементы ключевого столбца = 0, кроме разрезающего, он всегда равен 1.
• столбец, у которого в ключевой строке имеется 0,в новой таблице будет таким же.
• строка, у которой в ключевом столбце имеется 0, в новой таблице будет такой же.
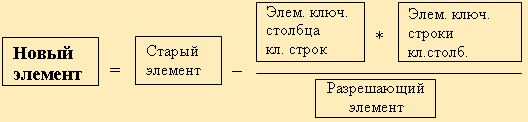
• в остальные клетки новой таблицы записывается результат преобразования элементов старой таблицы, как показано на рисунке 3.

Рисунок 3 – Составление нового элемента в симплекс-таблице В результате получают новую симплекс-таблицу, отвечающую новому базисному решению. Теперь следует просмотреть строку целевой функции (индексную), если в ней нет отрицательных значений (в задачи на нахождение максимального значения), либо положительных (в задачи на нахождение минимального значения) кроме стоящего на месте (свободного столбца), то значит, что оптимальное решение получено. В противном случае, переходим к новой симплекс таблице по выше описанному алгоритму. [7] Для решения задачи данной курсовой работы было выбрано направление задачи по оптимальному распределению средств на предприятии. Оптимальным планом или оптимальным решением задачи линейного программирования является план, при котором значение целевой будет возрастать (убывать). После анализа собранной информации, была составлена задача линейного программирования по цеху №8 в ОАО «НефАЗ».На покрасочном конвейере, на котором окрашиваются детали. Необходимо покрасить оптимальное количество деталей за одну рабочую смену, чтобы прибыль была максимальной. Для дальнейшего решения задачи необходимо составить постановку задачи и математическую модель задачи.

Источник

Метод Крамера

Определим оптимальную стратегию x = (x₁, x₂, x₃) игрока А и цену игры ν.

∆а = = 1·(-1)·(-4) + (-1)·1·2 — 1·2·2 = 4 — 2 — 4 = -2

Заменим 1-й столбец транспонированной матрицы А на вектор В. Найдем определитель полученной матрицы.

∆а₁ = = 1·(-1)(-4)+(-1)·1·2 — (-1)(-1)1 — 1·2·2 = 4 — 2 — 1 — 4 = -3

Заменим 2-й столбец транспонированной матрицы А на вектор результата В. Найдем определитель полученной матрицы.

∆а₂ = = 1·1·(-4) + (-1)·1·1 — 1·2·1 — 1·1·(-4) = -4 — 1 — 2 + 4 = -3

Заменим 3-й столбец транспонированной матрицы А на вектор результата В. Найдем определитель полученной матрицы.

∆a₃ = = 1·(-1)·1 + 1·1·2 — 1·1·2 = -1 + 2 — 2 = -1

Определим оптимальную стратегию y = (y₁, y₂, y₃) игрока B.

Заменим 1-й столбец матрицы А на вектор В. Найдем определитель полученной матрицы.

∆ã₁ = = 1·(-1)·(-4) + 1·2·1 — 1·2·2 — 1·1·(-4) = 4 + 2 — 4 + 4 = 6

Заменим 2-й столбец матрицы А на вектор результата В. Найдем определитель полученной матрицы.

∆ã₂ = = 1·1·(-4) + 1·2·(-1) — 1·2·1 = -4 — 2 — 2 = -8

Заменим 3-й столбец матрицы А на вектор результата В. Найдем определитель полученной матрицы.

∆ã₃ = = 1·(-1)·1+1·1·(-1) — 1·(-1)(-1) — 1·1·2 = -1 — 1 — 1 — 2 = -5

Ответ: Оптимальная стратегия игрока А x = ( ), оптимальная стратегия игрока В = ( ), y цена игры -2.

Биматричные игры

Игра имеет единственную ситуацию равновесия (P*,Q*), где оптимальными стратегиями являются: P* = ( ; ); Q* = ( ; ).

Игрок 1 должен использовать стратегии 1 и 2 с частотами и , а игрок 2 – стратегии 1 и 2 с частотами и .

Цена игры для первого игрока:

Цена игры для второго игрока:

Ответ: P* = ( ; ); Q* = ( ; ). Выигрыш игроков в равновесной ситуации: f(P*,Q*) = ( ; ).

Был получен навык решения стратегических задач, а именно антагонистических матричных и биматричных игр. Определена нижняя и верхняя цена игры, найдено решение в смешанных стратегиях матричной игры. Проведено сокращение размерности игры и найдено ее решение в смешанных стратегиях графическим методом, так же данная игра была оптимизирована в виде задачи линейного программирования. Решение проверено с помощью MS Excel, результаты получились одинаковые, что свидетельствует о правильности расчетов каждого метода. Были изучены метод Брауна-Робинсона и метод Крамера, а также решена биматричная игра графическим методом. \

Источник