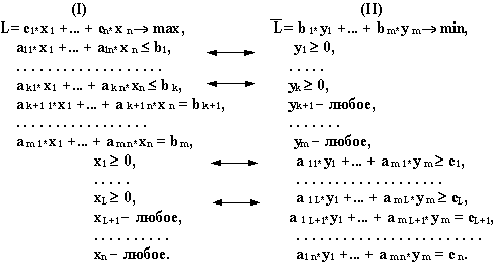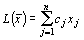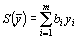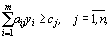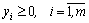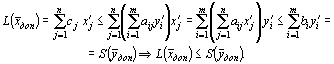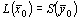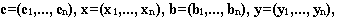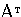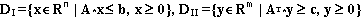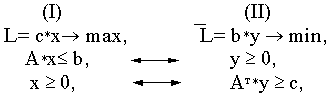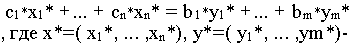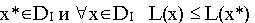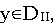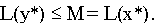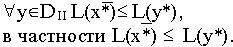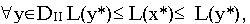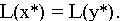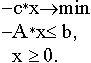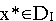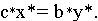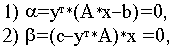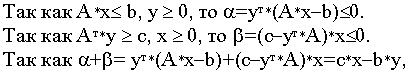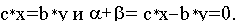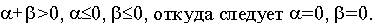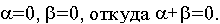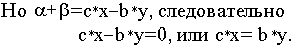Задаче линейного программирования соответствует двойственная задача

Содержание

9) Двойственные задачи. Двойственность в линейном программировании. Правила построения двойственных задач
Правила построения пары двойственных задач
Решение двойственной задачи линейного программирования

9) Двойственные задачи. Двойственность в линейном программировании. Правила построения двойственных задач

Двойственная задача линейного программирования — формальная модель задачи линейного программирования, симметричная к исходной постановке в части управляемых переменных, коэффициентов целевой функции и ограничений.

Для ряда практических задач линейного программирования целесообразно заменить решение исходной прямой задачи решением соответствующей двойственной задачи, симметричной исходной. Для любой прямой задачи линейного программирования можно сформулировать двойственную задачу следующим образом.

Прямая задача: CX -> min при условиях AX >= B X >= 0

Двойственная задача: YB -> max при условиях YA =< C Y >= 0

В приведенной матричной формулировке симметричность обеих задач очевидна. При этом также очевидно, что задача двойственная к двойственной есть исходная прямая задача. Таким образом, из данной пары можно считать любую задачу прямой, а другую двойственной.

Из сравнения обеих задач видно, что:

Если в исходной задаче имеется n переменных и m ограничений, то в двойственной m переменных и n ограничений.
Матрица коэффициентов ограничений двойственной задачи получается транспонированием соответствующей матрицы прямой задачи.
В правых частях ограничений каждой задачи стоят коэффиценты целевой функции, взятой из другой задачи.
Знаки неравенств функциональных ограничений обеих задач являются взаимно-обратными.
Если в прямой задаче требуется минимизация целевой функции, то в двойственной задаче требуется максимизация целевой функции.

Правила построения пары двойственных задач

Рассмотрим пару задач ЛП вида:

Задачу (I) называют прямой задачей ЛП, а (II) — двойственной. Ограничения задач (I) и (II), соответствующие друг другу (по стрелке), называются сопряженными. Заметим, что задача двойственная к (II), есть исходная прямая задача, т.е. соотношение двойственности взаимное. Поэтому можно любую из такой пары задач считать прямой, а другую двойственной.

Грубо говоря, двойственная задача — это на 90 0 повернутая исходная прямая задача. В этой связи полезно усвоить следующую схему соответствия.

10) Три леммы о двойственных задачах. Первая теорема двойственности. Следствия.

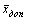
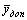
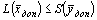
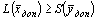
Лемма 1. Если и — произвольные допустимые решения пары двойственных задач, то , если исходная задача на максимум, и , если она на минимум.

Доказательство. Дана симметричная пара двойственных задач:

исходная задача: найти максимум функции

₍₄₎

и (5)

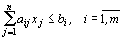
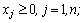
двойственная задача: найти минимум функции

₍₆₎

₍₇₎

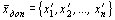
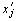
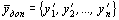
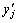
Пусть — допустимое решение исходной задачи, т.е. удовлетворяют неравенствам (5), — допустимое решение двойственной задачи, т.е. удовлетворяют неравенствам (7).

Аналогично рассматривается случай минимума.

Лемма 2. Достаточный признак оптимальности.

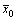
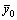
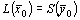
Если и — допустимые решения пары двойственных задач, для которых выполняется равенство , то и — оптимальные решения соответствующих задач.

Доказательство. Пусть и — допустимые решения пары двойственных задач, причем , и пусть исходная задача решается на максимум.

Возьмем произвольное допустимое решение исходной задачи , тогда по первой лемме . Получим т.е. , следовательно, — оптимальное решение исходной задачи. Аналогично доказывается, что — оптимальное решение двойственной задачи.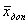

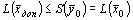
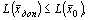
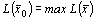
Рассмотрим пару симметрических двойственных задач в матричной форме записи

А- матрица из m строк и n столбцов, — транспонированная матрица. Введем обозначения для допустимых областей задачи (I) и (II)

Первая теорема двойственности

Рассмотрим пару симметричных двойственных задач

Первая теорема двойственности.

Если одна из пары двойственных задач (I) и (II разрешима, то разрешима и другая задача, причем оптимальные значения целевых функций прямой и двойственной задач совпадают

оптимальные планы задач (I) и (II) соответственно.

1. Пусть задача (I) разрешима, и пусть

т.е. х* — оптимальное решение. Обозначим M= L(х*).

Тогда по основной лемме существует

для которого

Но по основному неравенству двойственности имеем :

Объединяя последние два соотношения, имеем

откуда следует, что у* — оптимальное решение задачи (II) и

2. Пусть теперь задача (II) -разрешима. Построим эквивалентную (II) задачу

Задача (II’) разрешима, так как задача (II) разрешима. Тогда по пункту 1 двойственная к (II’) задача :

Но эта задача эквивалентна задаче (I). Следовательно, задача (I) разрешима.

Первый критерий оптимальности

Решение оптимально тогда и только тогда, когда существует решение

такое, что

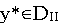
Необходимость следует из первой теоремы двойственности.

Достаточность следует из достаточного условия оптимальности.

11) Вторая теорема двойственности. Анализ чувствительности решений. Теорема о маргинальных значениях. Симплекс-множители.

Рассмотрим пару симметрических двойственных задач ЛП

Вторая теорема двойственности

Чтобы допустимые решения х, у пары двойственных задач (I) и (II) были оптимальными необходимо и достаточно, чтобы выполнялись условия :

Необходимость. По условию допустимые решения х, у — оптимальны.

то из оптимальности решений х, у по первой теореме двойственности

В результате имеем

По первой теореме двойственности получаем, что х, у — оптимальные решения задач (I) и (II).

Допустимые решения х, у задач (I) и (II) удовлетворяют условиям дополняющей нежесткости (УДН), если при подстановке этих векторов в ограничения задач (I) и (II) хотя бы одно из любой пары сопряженных неравенств обращается в равенство

Источник

Решение двойственной задачи линейного программирования

Инструкция . Выберите количество переменных и количество ограничений прямой задачи линейного программирования, нажмите Далее . Полученное решение сохраняется в файле Word и Excel . При этом ограничения типа x_i ≥ 0 не учитывайте. Если прямая задача ЛП не имеет решение, но требуется составить двойственную задачу или одна из переменных x_i неопределена, то можно использовать этот калькулятор.

Определив обратную матрицу А -1 через алгебраические дополнения, получим:
Как видно из последнего плана симплексной таблицы, обратная матрица A -1 расположена в столбцах дополнительных переменных x₄ , x₅ , x₆ .
Тогда Y = C*A -1 =
Оптимальный план двойственной задачи равен: y₁ = 23.75, y₂ = 12.5, y₃ = 0
Z(Y) = 1100*23.75+120*12.5+8000*0 = 27625
Подставим оптимальный план прямой задачи в систему ограниченной математической модели:
0.1*250 + 0.2*5375 + 0.4*0 = 1100 = 1100
0.05*250 + 0.02*5375 + 0.02*0 = 120 = 120
3*250 + 1*5375 + 2*0 = 6125 < 8000 1-ое ограничение прямой задачи выполняется как равенство. Это означает, что 1-ый ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y₁>0).
2-ое ограничение прямой задачи выполняется как равенство. Это означает, что 2-ый ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y₂>0).
3-ое ограничение выполняется как строгое неравенство, т.е. ресурс 3-го вида израсходован не полностью. Значит, этот ресурс не является дефицитным и его оценка в оптимальном плане y₃ = 0.
Таким образом, отличную от нуля двойственные оценки имеют лишь те виды ресурсов, которые полностью используются в оптимальном плане. Поэтому двойственные оценки определяют дефицитность ресурсов.
При постановке оптимальных двойственных оценок в систему ограничений двойственной задачи получим:
0.1*23.75 + 0.05*12.5 + 3*0 = 3 = 3
0.2*23.75 + 0.02*12.5 + 1*0 = 5 = 5
0.4*23.75 + 0.02*12.5 + 2*0 = 9.75 > 4
1-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 1-ый ресурс экономически выгодно использовать, а его использование предусмотрено оптимальным планом прямой задачи (x₁>0).
2-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 2-ый ресурс экономически выгодно использовать, а его использование предусмотрено оптимальным планом прямой задачи (x₂>0).
3-ое ограничение выполняется как строгое неравенство, т.е. ресурс 3-го вида использовать экономически не выгодно. И действительно в оптимальном плане прямой задачи x₃ = 0.
Величина двойственной оценки показывает, на сколько возрастает значение целевой функции при увеличении дефицитного ресурса на единицу.
Например, увеличении 1-го ресурса на 1 приведет к получению нового оптимального плана, в котором целевая функция возрастает на 23.75 и станет равной: F(x) = 27625 + 23.75 = 27648.75
Проведем анализ устойчивости оптимального плана и оценим степень влияния изменения ресурсов на значение целевой функции.
Пусть каждое значение параметра целевой функции изменится на ∆ с_i. Найдем интервалы, при которых будет экономически выгодно использование ресурсов.
1-ый параметр целевой функции может изменяться в пределах:

-3.8 ≤ с₁ ≤ 1
Таким образом, 1-параметр может быть уменьшен на 3.8 или увеличен на 1
Интервал изменения равен: [3-3.8; 3+1] = [-0.8;4]
Если значение c₁ будет лежать в данном интервале, то оптимальный план не изменится. 2-ый параметр целевой функции может изменяться в пределах:

-10 ≤ b₂ ≤ 30
Таким образом, 2-ый запас может быть уменьшен на 10 или увеличен на 30
Интервал изменения равен: [120-10; 120+30] = [110;150]
Составим субоптимальные варианты плана с учетом изменений исходных данных модели (таблицы).
Пусть 2-ый ресурс увеличили на 50

Базисные переменные	Значение базисных переменных	Коэффициент структурных сдвигов k c	Произведение k c на (50)	Расчет варианта плана
x 2	5375	6.25	312.5	5687.5
x 1	250	-2.5	-125	125
x 6	1875	1.25	62.5	1937.5
F(X)	27625	23.75	1187.5	28812.5

Пусть 1-ый ресурс уменьшили на -5

Базисные переменные	Значение базисных переменных	Коэффициент структурных сдвигов k c	Произведение k c на (-5)	Расчет варианта плана
x 2	5375	-12.5	62.5	5437.5
x 1	250	25	-125	125
x 6	1875	-62.5	312.5	2187.5
F(X)	27625	12.5	-62.5	27562.5

Задание : Для исходной задачи составить двойственную. Решить обе задачи симплексным методом или двойственным симплексным методом и по решению каждой из них найти решение другой. Одну из задач решить графическим методом.
F(X) = 3x₁ + x₂ → min
— 2x₁ + x₂≥4
2x₁ + x₂≤8
3x₁ + 2x₂≥6
Решение.
I этап. Приводим систему к каноническому виду.
II этап. Решаем симплекс-методом.
Примечание: Если задача решается данным калькулятором, то предыдущие два этапа пропускаем, поскольку они автоматически включены в решение.
На втором этапе окончательный вариант симплекс-таблицы имеет вид:

Базис	B	x₁	x₂	x₃	x₄	x₅	x₆	x₇
x₅	2	-7	0	-2	0	1	2	-1
x₄	4	4	0	1	1	0	-1	0
x₂	4	-2	1	-1	0	0	1	0
F(X3)	4	-5	0	-1	0	0	1-M	-M

Так как в оптимальном решении отсутствуют искусственные переменные (они равны нулю), то данное решение является допустимым. Записываем оптимальный план:
x₁ = 0, x₂ = 4, F(X) = 1•4 = 4 Составим двойственную задачу к прямой задаче.
— 2y₁ + 2y₂ + 3y₃≤3
y₁ + y₂ + 2y₃≤1
4y₁ + 8y₂ + 6y₃ → max
y₁ ≥ 0, y₂ ≤ 0, y₃ ≥ 0
Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи. Из теоремы двойственности следует, что Y = C*A -1 . Составим матрицу A из компонентов векторов, входящих в оптимальный базис.

Источник

A = (A₅, A₄, A₂) =