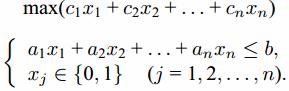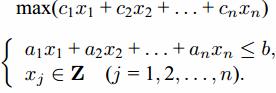Задача о рюкзаке
Задача о ранце
Имеются n предметов, которые необходимо поместить в рюкзак (ранец). Пусть известны вес aj и «ценность» cj каждого предмета (j= 1,2. ,n). Требуется заполнить рюкзак, не превышая его грузоподъемности (объема) b и максимизируя суммарную ценность груза. Получаем следующую булеву ЗЦЛП (задача о рюкзаке):
Задача о целочисленном рюкзаке
Предположим теперь, что каждый предмет имеется в неограниченном числе экземпляров, и требуется также максимизировать суммарную ценность груза, не превышая грузоподъемности. Получаем так называемую задачу о целочисленном рюкзаке:
Пример решения задачи о рюкзаке.
Задание. В рюкзак объема V = 7 кладут N = 5 предметов.Объемы, веса и количество предметов в каждой группе приведены в таблице.
| Объем | 1 | 2 | 3 | 1 | 1 |
| Вес | 2 | 3 | 2 | 4 | 1 |
| Кол-во | 1 | 3 | 3 | 1 | 2 |
Максимизировать общий вес рюкзака.
Решение. I этап. Условная оптимизация.
f1(L) = max(2x1); 0
Динамическое программирование — рюкзак, НВП, НОП
Предполагается, что вы уже знакомы с базовыми понятиями динамического программирования и помните бинарный поиск.
- Задача о рюкзаке
- НВП
- НОП
- Динамика по префиксу и значению последнего элемента
- Ленивая динамика
Задача о рюкзаке
0-1 Рюкзак
В самой простой форме задача о рюкзаке формулируется так: > Даны \(n\) предметов с весами \(a_1,\ldots,a_n\) . Определите, на какой максимальный вес можно набрать предметов в рюкзак вместимости \(W\) .
Для решения этой задачи воспользуемся динамическим программированием. Обозначим за \(dp[i][j]\) состояние, когда мы рассмотрели первые \(i\) предметов и набрали ими \(j\) веса. \(dp[i][j]=True\) , если такая ситуация возможна, иначе \(dp[i][j]=False\) .
Для каждого состояния \(dp[i][j]\) , которое возможно получить, мы можем либо взять предмет номер \(i\) и попробовать обновить ответ из состояния \(dp[i-1][j-a[i]]\) , либо не брать его и обновить ответ из \(dp[i-1][j]\) . Очевидно, что мы можем получить 0 веса, рассмотрев 0 предметов.
dp[0][0] = True for i in range(1, n + 1): for j in range(0, W + 1): dp[i][j] = dp[i - 1][j] if a[i] Ответом будет максимальное \(j\) , такое что \(dp[n][j]=True\) . Таким образом, мы получили решение за \(O(nW)\)
0-1 Рюкзак со стоимостями
Немного усложним задачу. Пусть, теперь предметы имеют не только веса, но и стоимости \(c_1,\ldots,c_n\) . Соответственно, надо набрать предметов с наибольшей суммарной стоимостью, но весом не превосходящим \(W\) . Теперь в \(dp[i][j]\) будем хранить не просто возможно ли получить из первых \(i\) предметов набор веса \(j\) , а максимальную суммарную стоимость такого набора. Если же такой набор получить невозможно, то по-прежнему \(dp[i][j]=0\) . Переходы такие же как и в прошлой задаче. Изначально \(dp\) заполнено 0, так как для любого непустого набора мы пока не знаем, как его получить, а путой набор имеет стоимость 0.
for i in range(1, n + 1): for j in range(0, W + 1): dp[i][j] = dp[i - 1][j] if a[i] Ответом на задачу будет максимальное \(dp[n][j]\) . Такое решение тоже работает за \(O(nW)\) .
Если так получилось, что веса большие, а стоимости маленькие, можно поменять их местами и считать минимальный вес при данной набранной стоимости. Поменять местами значение динамики и параметр — довольно распространенный трюк в динамическом программировании.
Рюкзак с ограниченным числом предметов
Пусть, теперь предметов каждого типа может быть несколько, то есть даны не только веса и стоимости, но и максимальные количества каждого из предметов \(k_1,\ldots,k_n\) . Тогда для каждого состояния \(dp[i][j]\) переберем, сколько мы взяли предметов такого типа и сделаем переход из каждого соответствующего состояния. Понятно, что мы не сможем взять более, чем \(\lfloor\frac\rfloor\) предметов каждого типа.
for i in range(1, n + 1): for j in range(0, W + 1): for cnt in range(min(k[i], W // a[i]) + 1): if a[i] * cnt Такое решение работает за \(O(nW^2)\) , так как \(k_i\) могут быть очень большими, а \(a_1=1\) .
Можете попробовать решить эту задачу за \(O(nW\log K)\) , где \(K\) — максимальное из \(k_i\) .
Рюкзак с неограниченным числом предметов
Пусть, теперь каждого предмета будет не \(k_i\) , а вообще бесконечно. Оказывается, задача стала только проще. Вернемся к обычному рюкзаку с весами и стоимостями. Единственное отличие будет в том, что теперь мы можем делать второй переход не из предыдущей строки, а прямо из текущей. При этом заметим, что для каждого состояния достаточно рассмотреть взятие только одного предмета данного типа, поскольку взятие двух и более будет рассмотрено одновременно.
for i in range(1, n + 1): for j in range(0, W + 1): dp[i][j] = dp[i - 1][j] if a[i] Такое решение работает за \(O(nW)\) .
Если \(W\) велико, а \(a_i\) достаточно малы, можно построить решение за \(O(n + A^3)\) , где \(A\) — максимальное из \(a_i\) . Заметим, что если \(W\) достаточно большое, то большая часть рюкзака будет занята предметами одного и того же типа с максимальной удельной стоимостью. Можно доказать, что одним и тем же предметом будет занято не менее \(W-A^2\) веса. Таким образом, можно за \(O(n)\) выбрать предмет с максимальным удельным весом, а для оставшихся предметов запустить предыдущий алгоритм, который сработает за \(O(A^3)\) , так как имеет смысл рассматривать не более \(A\) предметов, а максимальный вес \(A^2\) .
Восстановление ответа
Во всех рассмотренных задачах восстановление ответа делается стандартным образом: нужно из ответа пройтись обратно до начала.
- первый способ - это построить массив prev, где для каждой ячейки \(dp[i][j]\) хранить, берем мы предмет i, или не берем предмет \(i\) .
- второй способ - это определять это на ходу, смотря, какое из значений \(dp[i - 1][j]\) или \(dp[i - 1][j - a[i]] + c[i]\) больше.
Наибольшая возрастающая подпоследовательность
Пусть, дана последовательность из \(n\) чисел \(a_1,\ldots,a_n\) . Требуется найти длину ее наибольшей возрастающей подпоследовательности (НВП), то есть длину такой наибольшей последовательности индексов \(i_1 Пример: в последовательности \(100, \underline, \underline, 0, -40, \underline, -10, \underline, 110\) наибольшей возрастающей подпоследовательность является \(20, 75, 80, 120\) : она имеет длину \(4\) . Возрастающих подпоследовательностей длины 5 здесь нет. Давайте решать наивно через динамческое программирование - то есть хранить в \(dp[i]\) ровно то, что нам надо найти - длину НВП для первых \(i\) чисел. \(dp[0] = 0\) . Но как найти формулу, выражающую \(dp[i]\) через предыдущин значения? Ну, есть два варианта: * \(i\) -ое число не входит в НВП. Тогда \(dp[i] = 1\) * \(i\) -ое число входит в НВП. Тогда \(dp[i] = 1 + dp[k]\) , где \(k\) - индекс предыдущего числа в этой НВП. Так давайте просто его переберем. При этом надо учесть, что \(a[k]\) должно быть меньше, чем \(a[i]\) ! Итогвоая формула получается такая: Этот алгоритм работает за \(O(N^2)\) : у нас \(O(N)\) состояний динамики, и каждое из них мы считаем за \(O(N)\) действий, пока ищем этот максимум. Ответ восстанавливается тем же способом: для каждого состояния нужно сохранить, где был этот максимум - там и есть предыдущее число в НВП. Решим эту задачу чуть более нестандартным динамическим программированием, где \(min\_end[i]\) будет обозначать минимальное число, на которое может заканчиваться НВП длины \(i\) . При этом мы будем постепенно обрабатывать числа слева направо, и в этом массиве будет храниться только информация про все НВП в уже обработанном начале последовательности. Изначально \(min\_end[0]=-\infty, min\_end[i]=\infty\) для \(i>0\) . В качестве \(\infty\) надо выбрать число, которое заведомо больше любого из \(a_i\) , аналогично с \(-\infty\) . Рассматривая очередной элемент, попробуем продлить им каждую подпоследовательность: Ответом будет максимальный такой индекс \(j\) , что \(min\_end[j] \neq 0\) . Это решение работает за \(O(n^2)\) . Его можно значительно ускорить, заметив два факта: - На любом шаге \(min\_end[i-1]\leq min\_end[i]\) . Это легко доказать от противного. - Из предыдущего факта следует, что любое \(a[i]\) обновит максимум одно значение динамики, так как попадет максимум в один интервал. Значит, для поиска \(j\) , которое обновится можно воспользоваться бинарным поиском. Это решение уже работает за \(O(n\log n)\) . Даны две последовательности \(a_1,\ldots,a_n\) и \(b_1,\ldots,b_m\) . Требуется найти длину их наибольшей общей подпоследовательности (НОП), то есть длину наибольшей таких последовательностей \(i_1<\ldots Решим эту задачу с помощью динамического программирования, где \(dp[i][j]\) будет обозначать длину НОП, если мы рассмотрели префиксы последовательностей длины \(i\) и \(j\) . Тогда заметим, что есть две ситуации, когда мы считаем \(dp[i][j]\) : * \(a_i \neq b_j\) , тогда хотя бы один из этиз символов не содержится в НОП, иначе она заканчивается на два разных символа. В этом случае \(dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])\) * \(a_i = b_j\) , тогда несложно доказать, что точно есть максимальная НОП, в которую входят ОБА этих символа, а значит \(dp[i][j] = 1 + dp[i - 1][j - 1]\) . А на пустых префиксах ответ 0. Ответом является максимальное число в массиве \(dp\) . Решение работает за \(O(nm)\) . Ответ при это восстанавливается классическим способом - с конца. Нам все еще нужно просто в каждой ячейке смотреть - если символы в ней равны, то нужно уменьшить \(i\) и \(j\) , иначе только один из них - так, чтобы НОП был максимален. Сведите задачу НВП к задаче НОП. Найдите НОП двух перестановок длины \(n\) за \(O(n\log n)\) . Пусть, дана последовательность \(a_1,\ldots,a_n\) , с максимальным значением \(A\) . Требуется найти длину наибольшей такой подпоследовательности, что ее элементы отличаются на более, чем на 1. Воспользуемся динамическим программированием, где \(dp[j]\) будет обозначать ответ с последним взятым элементом, равным \(j\) . Будем обновлять и хранить актуалььным весь массив \(dp\) целиком, проходясь по массиву \(a\) слева направо. Соответственно для каждого \(i\) переходы можно делать только из таких \(j\) , что \(|a[i]-j|\leq 1\) . Заметим, что вот эти две идеи встречаются в задачах наиболее часто: * хранить в \(dp[i]\) ответ для \(i\) -ого префикса. Как в рюкзаке (где можно пользоваться \(i\) первыми предметами), НВП(где ответ на префиксе длины \(i\) ) и НОП (где ответ для префиксов длины \(i\) и \(j\) ). * хранить в \(dp[i]\) ответ для последовательностей, заканчивающихся на \(i\) . Если сложно придумать порядок обхода таким образом, чтобы все предыдущие значения уже были посчитаны, то можно вместо циклов использовать рекурсивную функцию и запоминать посчитанный результат, чтобы не считать несколько раз одно и то же. Решим, например, обычную задачу о рюкзаке таким образом. Изначально все \(dp[i][j]=-1\) , это будет обозначать, что значение еще не посчитано, кроме \(dp[0][j]=0\) . Время работы так же составит \(O(nW)\) , так как каждое значение мы считаем только один раз, но истинное время работы будет в несколько раз больше, потому что константа на вызовы функции значительно выше чем на простой цикл. Решите как можно больше задач из этих двух контестов:НВП за \(O(N^2)\)
НВП за \(O(N\log)\)
n = 6 a = [6, 1, 5, 3, 4, 2] # НВП: 1, 3, 4 inf = 100 min_end = [-inf] + [inf] * n for i in range(n): for j in range(n): if min_end[j - 1] < a[i] < =min_end[j]: min_end[j] = a[i] print(dp)--------------------------------------------------------------------------- NameError Traceback (most recent call last) in () 7 if min_end[j - 1] < a[i] < min_end[j]: 8 min_end[j] = a[i] ---->9 print(dp) NameError: name 'dp' is not definedНаибольшая общая подпоследовательность
a = [1, 100, 2, 100, 3] b = [10, 10, 1, 2, 3, 10] # НОП: 1,2,3 n = len(a) m = len(b) dp = [[0 for j in range(m + 1)] for i in range(n + 1)] for i in range(1, n + 1): for j in range(1, m + 1): dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) if a[i - 1] == b[j - 1]: dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + 1) print(dp[i])[0, 0, 0, 1, 1, 1, 1] [0, 0, 0, 1, 1, 1, 1] [0, 0, 0, 1, 2, 2, 2] [0, 0, 0, 1, 2, 2, 2] [0, 0, 0, 1, 2, 3, 3]Задание
Задание
Динамика по префиксу и значению последнего элемента
for i in range(1, n + 1): dp[a[i]] += 1 if a[i] > 0: dp[a[i]] = max(dp[a[i]], dp[a[i] - 1] + 1) if a[i] < A: dp[a[i]] = max(dp[a[i]], dp[a[i] + 1] + 1)Ленивая динамика
def calc(i, j): if dp[i][j] == -1: dp[i][j] = calc(i - 1, j) if a[i] Задание