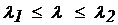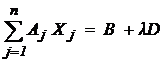Задача параметрического программирования пример

Задачи параметрического программирования

Параметрическое программирование представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или нескольких параметров t .

Инструкция . Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word . При этом ограничения типа x_i≥0 не учитывайте.

С математической точки зрения параметрическое программирование выступает как одно из средств анализа чувствительности решения к вариации исходных данных, оценки устойчивости решения.

Алгоритм решения задач параметрического линейного программирования

1. Считая значение параметра λ равным некоторому числу λ ₀ ∈ [α, β], находим оптимальный план Х * или устанавливаем неразрешимость полученной задачи линейного программирования.
2. Определяют множество значений параметра λ, для которых найденный оптимальный план является оптимальным или задача неразрешима. Эти значения параметра исключаются из рассмотрения.
3. Полагают значение параметра λ равным некоторому числу, принадлежавшему оставшейся части промежутка [α, β], и находят решение полученной задачи линейного программирования.
4. Определяют множество значений параметра λ, для которых новый оптимальный план остается оптимальным или задача неразрешима. Вычисления повторяются до тех пор, пока не будут исследованы все значения параметра λ ∈ [α, β].

Источник

2.6 Параметрическое линейное программирование

Параметрическое программирование представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или нескольких параметров.

Необходимость рассмотрения подобных задач обусловлена различными причинами. Одной из основных является та, что исходные данные для численного решения любой реальной задачи оптимизации в большинстве случаев определяются приближенно или могут изменяться под влиянием каких-то факторов, что может существенно сказаться на оптимальности выбираемой программы (плана) действий. Соответственно, разумно указывать не конкретные данные, а диапазон возможного изменения данных, чтобы в результате решения иметь наилучшие планы для любого варианта исходных данных.

С математической точки зрения параметрическое программирование выступает как одно из средств анализа чувствительности решения к вариации исходных данных, оценки устойчивости решения.

Заметим, что существуют различные подходы к подобному анализу (например, на основе постановки двойственной задачи). Здесь мы, не ссылаясь на двойственные оценки, рассмотрим самые простейшие варианты решения для самых простейших параметрических программ.

Рассмотрим задачу параметрического линейного программирования, в которой только коэффициенты целевой функции линейно зависят от некоторого единственного параметра λ(времени, температуры и т. п.):

Отыскать максимум (или минимум) функции:

, X_j ≥ 0,

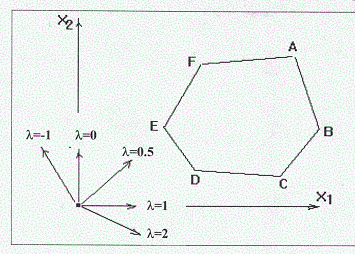
Если обратиться к геометрической интерпретации задачи, то можно заметить, что вектор-градиент линейной формы определяется её параметром. Например, для целевой функции L(X, λ) = λX₁ + (1-λ)X₂ при различных значениях параметра λ градиент определяет различные направления роста функции.

Нетрудно видеть, что, если при некотором значении параметра максимум достигается в вершине A, то небольшая вариация этого значения несколько изменит направление градиента, но не изменит положение точки максимума. Отсюда напрашивается вывод, что некоторый план, оптимальный при λ = λ₀ оптимален и в окрестности λ₀, т.е. при α ≤ λ ≤ β где λ₀ ∈ [α, β].

Можно заметить, что при градиенте, ставшем перпендикулярным некоторой стороне многоугольника планов, имеем два разных оптимальных опорных плана с одним и тем же значением линейной формы, откуда можно утверждать непрерывность экстремума линейной формы по λ

В случае неограниченности множества планов можно утверждать, что если линейная форма не ограничена при λ = λ₀, то она не ограничена при всех λ, больших или меньших λ₀.

Алгоритм для решения задач параметрического линейного программирования в случае зависимости от параметра коэффициентов целевой функции незначительно отличается от обычного симплексного метода (примеры решения подобных задач приведены ниже).

В случае зависимости от параметра компонент вектора правых частей ограничений, т. е. решения задачи поиска экстремума функции

, X_j ≥0, j = 1 . n;

Во избежание сложностей, связанных с требованием сохранения неотрицательности компонент плана при любых λ (сохранения неотрицательности правой части системы уравнений при всех ее тождественных преобразованиях), достаточно постановить двойственную задачу, воспользоваться вышеупомянутым алгоритмом решения задач параметрического линейного программирования при зависимости от параметра коэффициентов целевой функции и с помощью известных двойственных соотношений находить решение исходной задачи.

Источник

Параметрическое линейное программирование

В настоящий момент дополнительные накопительные скидки (от 2% до 25%) предоставляются 58.234 образовательным учреждениям . Чтобы узнать, какая скидка действует для всех сотрудников Вашего образовательного учреждения, войдите в свой личный кабинет «Инфоурок».

Курс повышения квалификации

Специалист в области охраны труда

К данной скидке мы можем добавить скидку Вашего образовательного учреждения (она зависит от того, сколько Ваших коллег прошло курсы «Инфоурок»)

В настоящий момент дополнительные накопительные скидки (от 2% до 25%) предоставляются 58.234 образовательным учреждениям . Чтобы узнать, какая скидка действует для всех сотрудников Вашего образовательного учреждения, войдите в свой личный кабинет «Инфоурок».

Курс профессиональной переподготовки

Организация деятельности библиотекаря в профессиональном образовании

К данной скидке мы можем добавить скидку Вашего образовательного учреждения (она зависит от того, сколько Ваших коллег прошло курсы «Инфоурок»)

В настоящий момент дополнительные накопительные скидки (от 2% до 25%) предоставляются 58.234 образовательным учреждениям . Чтобы узнать, какая скидка действует для всех сотрудников Вашего образовательного учреждения, войдите в свой личный кабинет «Инфоурок».

Оценка эффективности тренинга

Описание презентации по отдельным слайдам:

1 слайд Параметрическое линейное программирование
Выполнила: студентка
3 курса, группы ММ-61
Лучинина Екатерина
Проверил: Щиканов
Алексей Юрьевич

2 слайд Параметрическое линейное программирование представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или нескольких параметров.
С математической точки зрения параметрическое программирование выступает как одно из средств анализа чувствительности решения к вариации исходных данных, оценки устойчивости решения.
Сущность задачи параметрического ЛП

3 слайд Геометрическая интерпретация задачи параметрического ЛП
Если обратиться к геометрической интерпретации задачи, то можно заметить, что вектор-градиент линейной формы определяется её параметром. Например, для целевой функции L(X, λ) = λX1 + (1-λ)X2 при различных значениях параметра λ градиент определяет различные направления роста функции.
Нетрудно видеть, что, если при некотором значении параметра максимум достигается в вершине A, то небольшая вариация этого значения несколько изменит направление градиента, но не изменит положение точки максимума. Отсюда напрашивается вывод, что некоторый план, оптимальный при λ = λ0 оптимален и в окрестности λ0, т.е. при α ≤ λ ≤ β где λ0 [α, β].

5 слайд Алгоритм решения задачи параметрического ЛП
Считая значение параметра равным некоторому числу , находим оптимальный план Х* или устанавливаем неразрешимость полученной задачи линейного программирования.
Определяют множество значений параметра , для которых найденный оптимальный план является оптимальным или задача неразрешима. Эти значения параметра исключаются из рассмотрения.
Полагают значение параметра равным некоторому числу, принадлежавшему оставшейся части промежутка, и находят решение полученной задачи линейного программирования.
Определяют множество значений параметра , для которых новый оптимальный план остается оптимальным или задача неразрешима. Вычисления повторяются до тех пор, пока не будут исследованы все значения параметра .

6 слайд Пример задачи параметрического ЛП
Предприятие должно выпустить два вида продукции А и В, для изготовления которых используется три вида сырья, нормы расходов заданы в таблице. Известно, что цена на А единицу продукции может изменяться от 2 до 12 у.е., для В от 13 до 3 у.е. Найти оптимальные планы выпуска для заданных интервалов цен.

Строим систему ограничений, находим целевую функцию:

8 слайд В соответствии с ограничениями и полученными параметрами строим первую симплекс таблицу:
Решение начинаем при

10 слайд При решение найдено. Найдем интервал изменения , при котором решение будет оставаться оптимальным.

При > выбранный столбец является разрешающим. Для нахождения нового оптимального решения при >

Источник