Задача математического моделирования python

Методы имитационного моделирования вероятностных распределений на языке программирования Python

В данной статье рассмотрим методы имитационного моделирования на основе теории систем массового обслуживания, в которых широко используются элементы математической статистики и теории вероятностей. Целью данной статьи является разработка методов, которые можно использовать для создания моделей, в основе которых фигурируют вероятностные распределения и элементы массового обслуживая.

Прежде, чем приступить к разработке методов, определим ключевые подходы, которые мы будем использовать в процессе: генерация случайных величин, вероятностные распределения, а также некоторые элементы теории вероятностей и математической статистики. В результатах опытов увидим экспериментальную демонстрацию поведения вероятностных распределений и имитации случайных процессов. Всё это и даст нам инструментальную основу для создания различных имитационных моделей, в которых фигурируют вероятностные распределения.

Все методы моделирования данного исследования представлены на программном языке Python. Этот язык является распространённым инструментов в сфере научных исследований и сфере обучения.

В дальнейших этапах исследования, которые будут представлены в будущих статьях, перейдём к более сложным экспериментам: рассмотрим вероятностные распределения, которые не вошли рамки данной статьи, рассмотрим имитационное моделирования систем и сетей массового обслуживания, и также продемонстрируем программирование подобных моделей с использованием параллельных вычислений.

Методы моделирование случайных величин и генераторы случайных чисел python

Рассмотрим простые модели подбрасывания одного или нескольких игральных кубиков. Моделирование начнём с генерации случайных чисел. Задача генерации чисел и вопросы об истинной и квази-случайности в наши исследования не входят, но Вы можете найти данные обсуждения в других источниках. В наших моделях используется генератор псевдо-случайных величин Python. На начальном этапе, для наглядности изучения, можно повышать количество испытаний, наблюдая результат моделирования.

Начнём с генерации случайных величин. Методы их генерирования сводятся к использованию стандартных библиотек Python.

Модуль random из стандартной библиотеки предоставляет возможность получения случайных вещественных чисел в диапазоне от 0 до 1, случайных целых чисел в заданном диапазоне, случайного выбора элементов последовательности и многое другое:
Модуль random может использоваться, например, для перемешивания колоды карт в игре, случайного выбора изображения в программе демонстрации слайдов, в программах статистического моделирования и так далее. За дополнительной информацией обращайтесь к руководству по стандартной библиотеке языка Python.

Расширение NumPy, содержащее реализацию математических вычислений для Python благодаря комбинированию компилированных и оптимизированных библиотек расширения с языком Python NumPy превращает Python в мощный, эффективный и удобный инструмент математических вычислений.

Подробное описание модуля NumPy вы найдёте в официальной документации по этому пакету.

Методы моделирование вероятностных распределений с помощью python

Приступим к моделированию: будем подбрасывать игральный кубик. Ниже представлен листинг программирования модели подбрасывания одного кубика (рис.1). Кубик может принимать одно из шести значений.

import pylab import numpy # Количество испытаний trials = 500 # Массив значений values = numpy.random.randint(1, 7, size=trials) pylab.hist(values, bins=[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5], edgecolor='white') pylab.xlabel('Значение') pylab.ylabel('Количества раз') pylab.title('Подбрасывание кубика ' + str(trials) + ' раз') pylab.show() 

Рис.1. Листинг программирования модели подбрасывания одного кубика

В представленной программе задаём количество испытаний: сколько раз подбрасывается кубик, и массив: какое значение выпадает в каждом испытании. Результат выводим в виде гистограммы (рис.2).

Рассматривая результат, можно предположить, что распределение имеет равномерный характер. Увеличив число испытаний до 10 000 раз можно увидеть, что гистограмма имеет вид, подобный гистограмме равномерного распределения.

Следующим испытанием рассмотрим модель подбрасывания двух игральных кубиков. Код программы при этом незначительно измениться (рис.3).

Рис.2. Результаты моделирования подбрасывания одного кубика

. # Массив значений values = [] for i in range(trials): values.append(numpy.random.randint(1, 7) + numpy.random.randint(1, 7)) pylab.hist(values, bins=[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5, 10.5, 11.5, 12.5, 13.5], facecolor='green', edgecolor='white') . 

Рис.3. Часть изменённого листинга для программирования модели подбрасывания двух кубиков

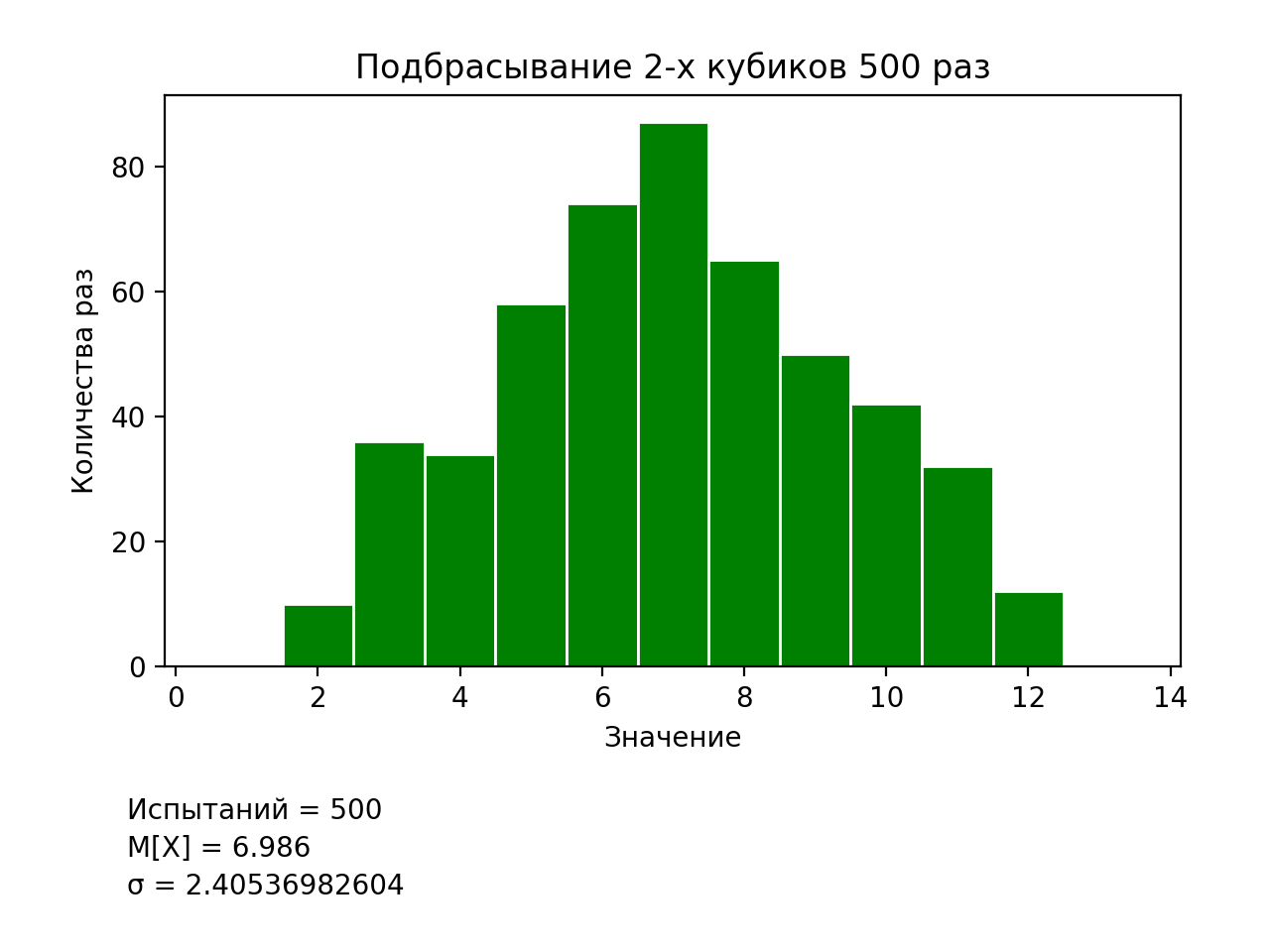
В представленном листинге значительным изменением является присвоение значения массиву, в который записываем выпавшие значения уже двух кубиков. Вторым изменением, менее значительным, является представления гистограммы соответствующих вариантов значений. Результат выполнения программы представлен на рис.4.

Получив результат моделирования подбрасывания двух кубиков рассмотрим задачу моделирования нормального (Гаусс) распределения и насколько она коррелирует с задачей моделирования подбрасывания нескольких кубиков. Код программы также меняется незначительно: меняется всего одна строка присваивания значений массиву (рис.5).

Рис.4. Результаты моделирования подбрасывания двух кубиков

. # Массив значений values = [] for i in range(trials): mu = 7 sigma = 2.4 values.append(random.normalvariate(mu, sigma)) . 

Рис.5. Часть изменённого листинга для программирования модели нормального распределения

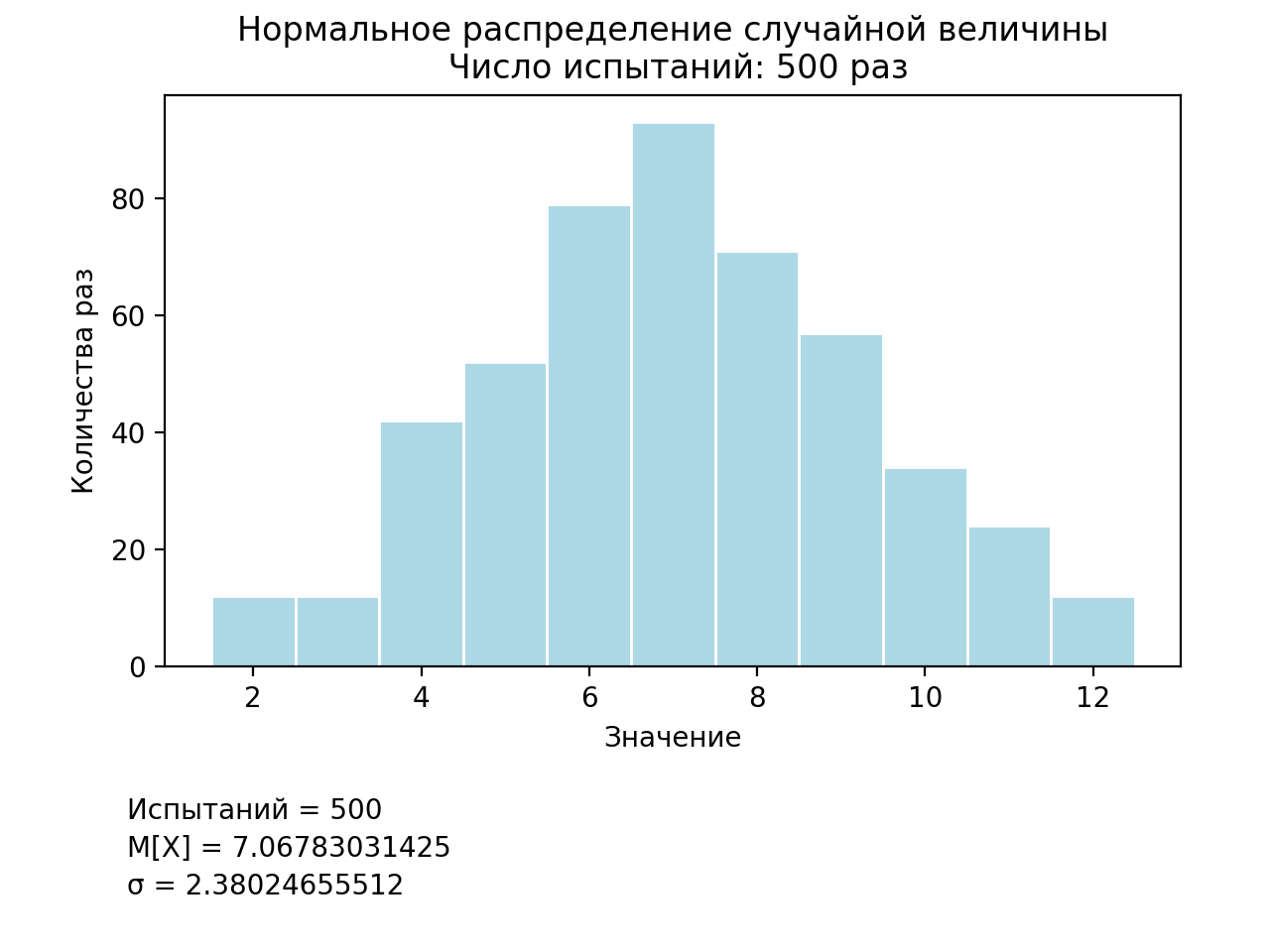
На представленном листинге используется метод normalvariate библиотеки random, генерирующий величины с нормальным вероятностным распределением со параметрами mu и sigma, которые являются среднем значением и стандартным отклонением распределения соответственно. Результат выполнения программы представлен на рис.6.

Рис.6. Результаты моделирования нормального распределения

Заключительным этапом является моделирование экспоненциального распределения. Экспоненциальное распределение часто используется при моделировании распределения (длительности) интервалов между моментами поступления заявок в системах массового обслуживания разного типа. Листинг также отличается незначительно от остальных листингов программ, представленных в нашем исследовании (рис.7).

Результат моделирования представлен на рис.8.

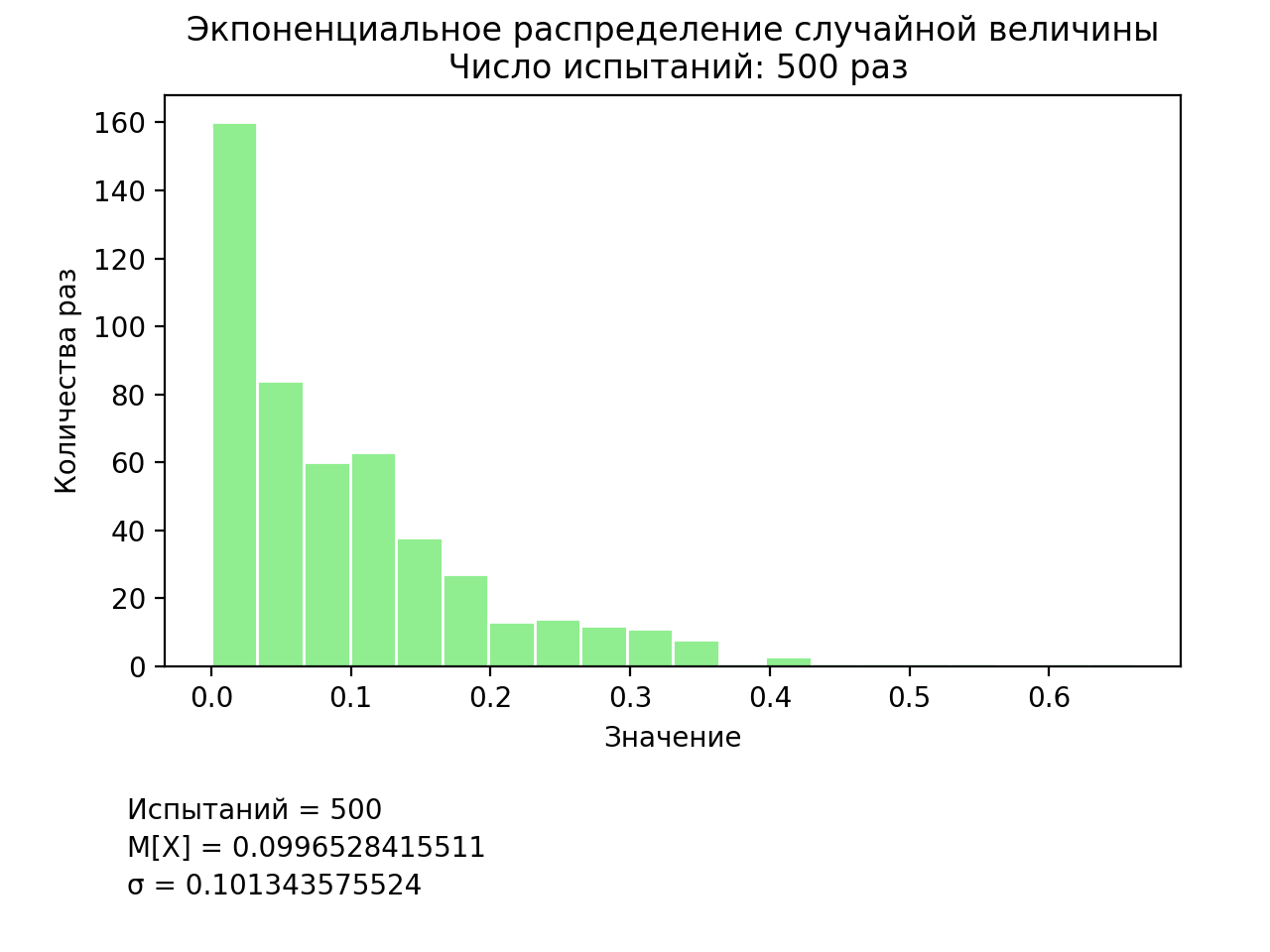
. lambd = 10 # Массив значений values = [] for i in range(trials): values.append(random.expovariate(lambd)) pylab.hist(values, 20, facecolor='lightgreen', edgecolor='white') . 

Рис.7. Часть изменённого листинга для программирования модели экспоненциального распределения

Рис.8. Результаты моделирования экспоненциального распределения

Заключение

В этой статье были рассмотрены несколько программных реализаций моделей вероятностных распределений на языке Python. Эти модели дают основу для проведения собственных экспериментов и исследований.

На данном этапе представлены только некоторые методы и подходы, и в дальнейшем, автор представит дополнительные методы для моделирования с использованием вероятностных распределений, языка программирования Python и теории массового обслуживания.

Источник

Русские Блоги

Математические модели и применение Python для научных вычислений (1): краткое описание математических моделей, краткое описание Python для научных вычислений

Это новая глава, математическая модель и приложение Python для научных вычислений. Учебник по математическому моделированию, соответствующий этой статье, является пятым изданием «Математической модели» издания о высшем образовании (под редакцией Цзяна Циюаня, Се Цзиньсина, Е июня). В серии текстов вместо matlab будет использоваться python, а используемая библиотека python — Nump (используется для Операции с массивами), Matplotlib (для визуализации 2D-данных), Scipy (продвинутые научные вычисления), Mayavi (3D-графика) и т. Д. В качестве учебного пособия используется учебник по китайскому тексту Scipy, опубликованный в сообществе Github.

Краткое описание математической модели

Что такое математическая модель?

Один для реального мираКонкретный объект, Для одногоКонкретное назначениеСогласноВнутренний законИ сделать некоторыеУпростить гипотезуИспользоватьМатематические инструментыИ получитьМатематическая структура。

Процесс математического моделирования:

Основные этапы математического моделирования:

• Подготовка модели: понять реальные проблемы, уточнить цель и собрать важную информацию, такую ​​как явления и данные. Форма относительно понятный вопрос.
• Модель предположения: в соответствии с характеристиками и целью определить сущность, устранить другие факторы, сделать необходимые, разумные и упрощенные предположения
• Композиция модели: с использованием математического описания языка обозначений
• Решение модели: использование математических методов для решения
• Анализ модели: выполнить анализ ошибок, статистический анализ, анализ чувствительности, анализ надежности
• Проверка модели: сравнение с актуальными проблемами
• Модель приложения: применяется к актуальным

Весь процесс математического моделирования:

Как показано:

Python научная вычислительная экология:

Почему выбирают питона?

Матлаб болит:

• Преимущества:
  • Существует очень библиотека классов для различных алгоритмов в разных областях. Реализация быстрая, потому что эти библиотеки обычно
    Написано на скомпилированном языке.
  • Дружественная среда разработки: полная, хорошо организованная помощь, встроенный редактор и т. Д.
    имеет коммерческую поддержку
  • Базовый язык очень не хватает и будет ограничивать опытных пользователей
  • Не бесплатно
  • Большой инсталляционный пакет заставляет людей рвать кровью

  Недостатки python относительно matlab:

  • Не очень дружелюбная среда разработки, такая как по сравнению с Matlab.
  • Не все алгоритмы можно найти в других профессиональных программах или наборах инструментов

  Python для научной вычислительной среды

  • Здесь используется Spyder. Сначала устанавливается Anaconda. После завершения установки некоторые библиотеки будут автоматически интегрированы. Spyder — интегрированный текстовый редактор Py в Anaconda
  • Spyder использует интерфейс программирования Matlab и отображает переменные.

  Введение и использование spyder:

  Некоторые основные операции:

  После установки Spyder в меню «Пуск» появится программа Spyder, нажмите, чтобы открыть, как показано на рисунке:
  
  
  Может пожелать ввести в интерактивном окне записи:

  Результаты показаны на рисунке:
  
  Импортируйте библиотеку здесь, чтобы увидеть, есть ли какие-либо ошибки:
  
  Если ошибок нет, проблем нет.
  Посмотрите на создание переменной a:
  
  В это время в окне информации о переменной будет отображаться:
  
  Используйте «очистить», чтобы очистить команду
  
  Но переменные не ясны. Чтобы изменить переменные, один метод должен изменить код, а другой — изменить интерфейс:

  

  • Выберите переменную и щелкните правой кнопкой мыши, чтобы изменить
  • Нажмите кнопку настройки в интерактивном окне, чтобы сбросить все переменные одним щелчком мыши.

  Используйте текст для написания и запуска текста:

  1. Отредактируйте код в окне редактирования текста и сохраните его в каталоге, который вы хотите сохранить
  2. Используйте в интерактивных окнах ls Просмотр подкаталогов или файлов в текущем каталоге, используйте cd Чтобы изменить путь к файлу, используйте run + Запустите файл. Такие как:

  # -*- coding: utf-8 -*- """ Created on Wed Sep 4 16:24:52 2019 @author: Administrator """ # Создайте файл py с именем «my_file.py» в научном файле на диске E s = "Привет!" print(s) 

  
  
  Переменная «s» также появится в окне переменных
  

  На этот раз содержание заканчивается здесь

  Источник