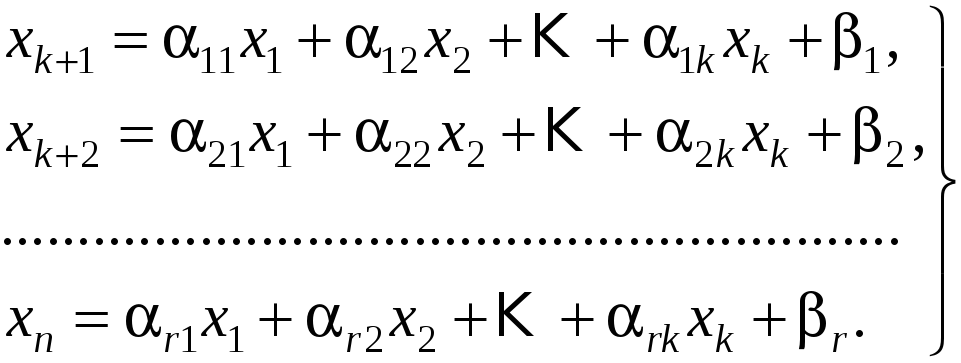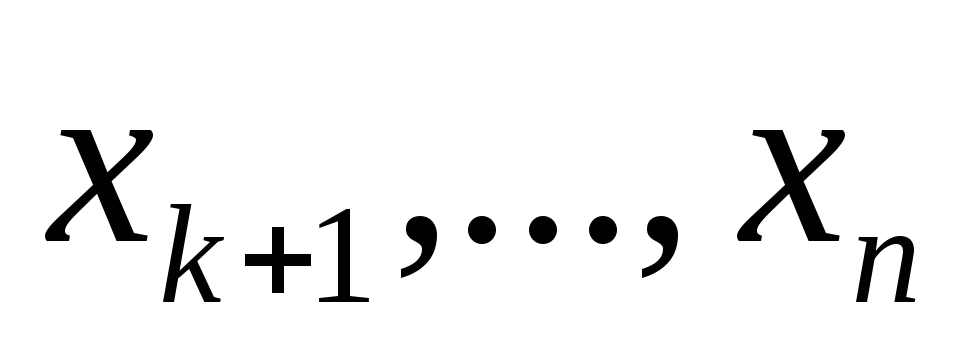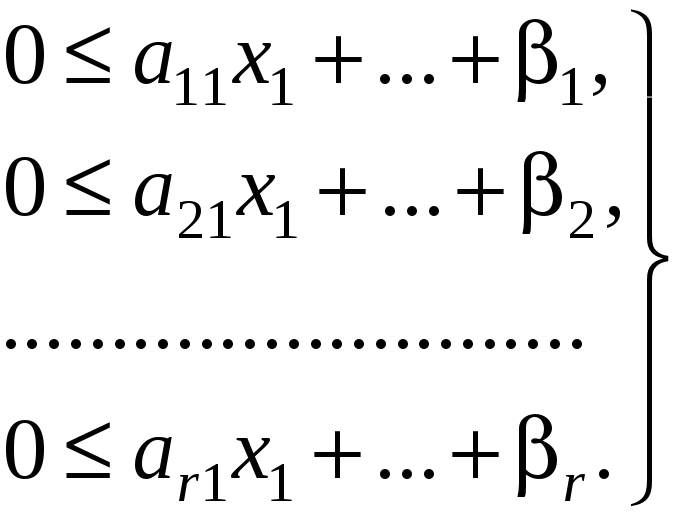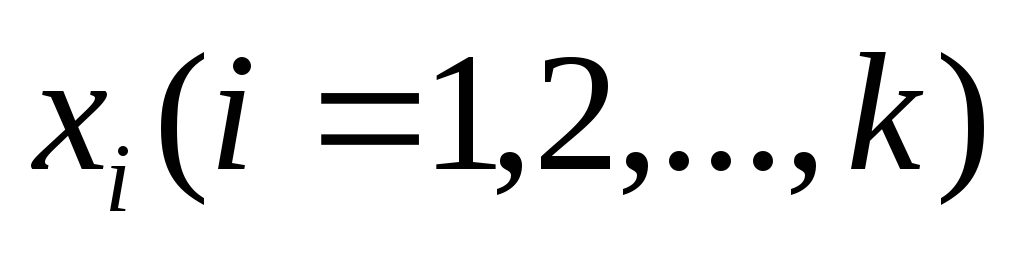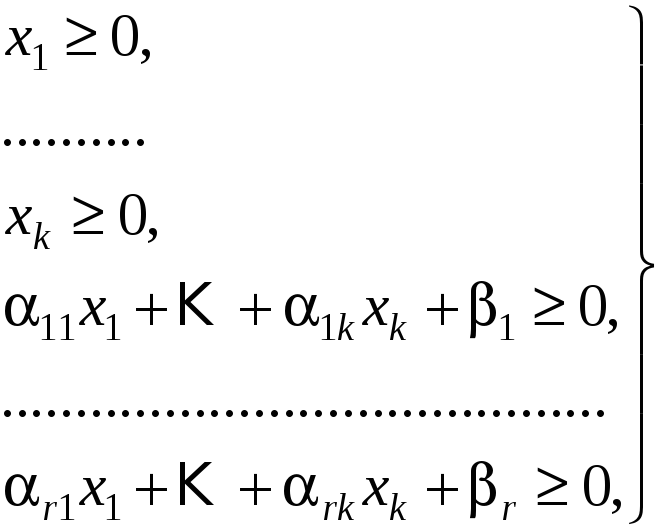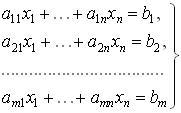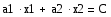Задача линейного программирования при ограничениях неравенствах

Задача линейного программирования с ограничениями-неравенствами. Переход от нее к основной задаче линейного программирования и наоборот

На практике ограничения в задаче линейного программирования часто задаются не уравнениями, а неравенствами.

Покажем, как можно перейти от задачи с ограничениями-неравенствами к основной задаче линейного программирования.

Пусть имеется задача линейного программирования с п переменными х_р х₂. х_п, в которой ограничения, наложенные на переменные, имеют вид линейных неравенств. В одних ограничениях знак неравенства может быть >, в других ПРИМЕР 3.3. Имеется задача линейного программирования с ограничениями-равенствами (ОЗЛП)

и минимизируемой функцией

Требуется записать ее как задачу линейного программирования с ограничениями-неравенствами и построить ее решение.

Решение. Так как т = 3, п = 5, п — т = 2, выберем какие-то две из переменных в качестве свободных. Заметим, что переменные лг, х₂ в качестве свободных выбирать нельзя, так как они связаны первым из уравнений (3.22): значение одной из них полностью определяется значением другой, а свободные переменные должны быть независимыми. По такой же причине нельзя в качестве свободных выбрать переменные х₂, х₃ [их связывает второе уравнение (3.22)]. Выберем в качестве свободных переменные х₁их₄и выразим через них все остальные:

Так как х₂ > 0, х₃ > 0, х₅ > 0, условия (3.24) могут быть заменены неравенствами:

Перейдем в выражении линейной функции L к свободным переменным х,, х₄. Подставив в L вместо х₂ и х₅ их выражения (3.24), получим

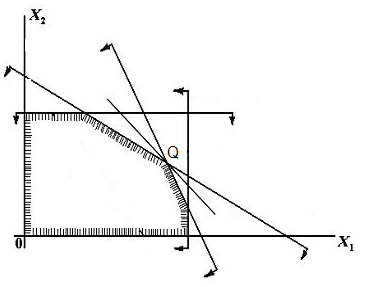
Таким образом, задача сведена к задаче линейного программирования с ограничениями-неравенствами. Ее геометрическая интерпретация показана на рис. 3.3. Основная прямая V — 0 параллельна той стороне ОДР, где L’ достигает минимума. Следо-

вательно, все точки участка ЛВ дают оптимальное решение. Выбрав в качестве решения, например, координаты точки А, получим

При таких значениях переменных линейная функция L достигает минимума, равного

Таким образом, мы можем произвольно переходить от ОЗЛП к задаче линейного программирования с ограничениями-неравенствами и наоборот. Если в числе ограничений задачи есть как уравнения, так и неравенства, рекомендуется произвести унификацию, т.е. перейти к какой-либо единообразной форме, например к ОЗЛП.

ОПРИМЕР 3.4. Имеется задача линейного программирования с переменными jc, х₂, х_у х₄ и ограничениями вида

Минимизируется функция Требуется привести задачу к ОЗЛП.

Решение. Введением добавочных переменных y_v у₂ приведем условия (3.27) к виду ОЗЛП:

Минимизируемая функция остается в виде (3.28). ?

Источник

18. Линейное программирование. Преобразование основной задачи к основной задаче лп с ограничениями-неравенствами (форма а).

(*)и рассмотрим случай (r – ранг системы, n – число неизвестных). Из линейной алгебры известно, что в этом случае r неизвестных линейно выражаются через остальные неизвестных (эти последние принято называть свободными). Всегда можно занумеровать неизвестные так, чтобы последние выразились через первые (поскольку , то неизвестных в точности r штук).

(**)

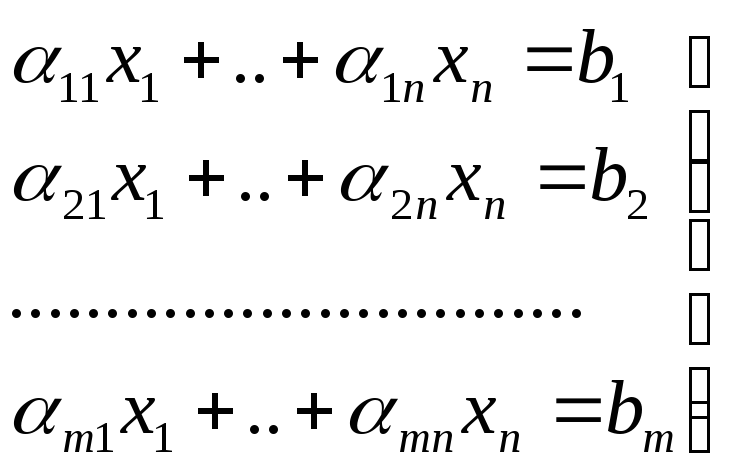
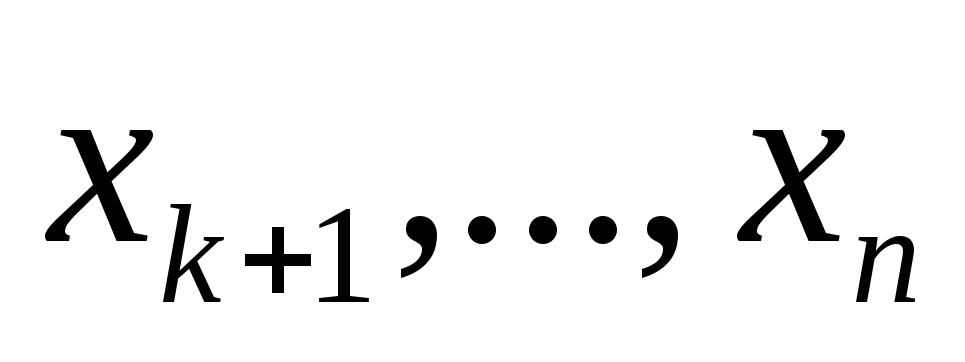
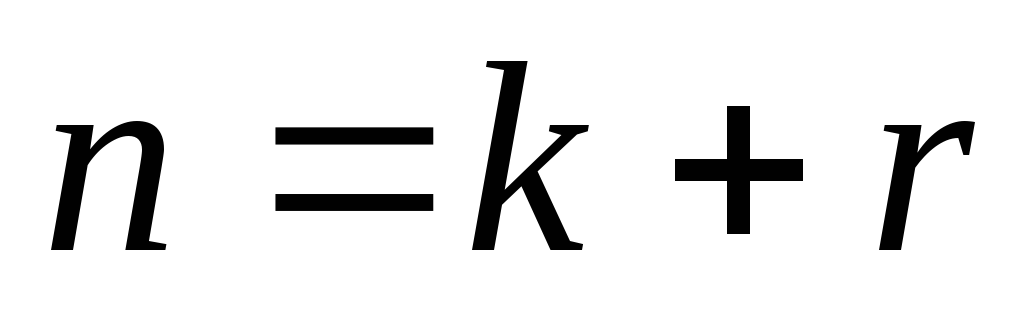
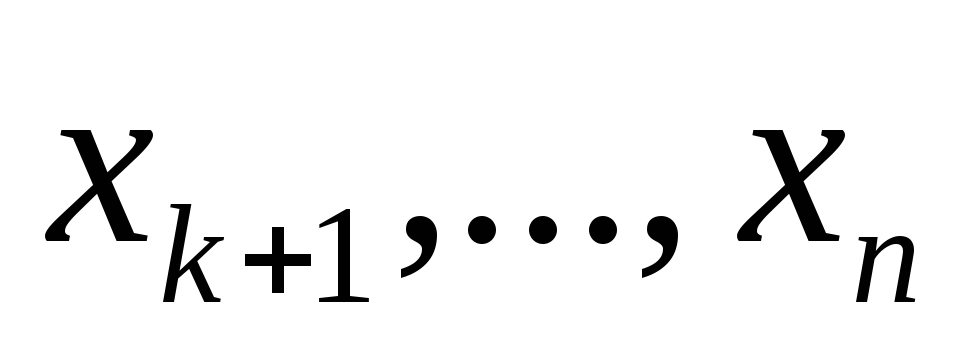
Полученная система эквивалентна системе основной задачи.

Если теперь вместо величин в выражении для формы F подставить их значения из полученной систеиы, то форма F примет другой вид:

, она по-прежнему остается линейной, но выражается только через свободные неизвестные .

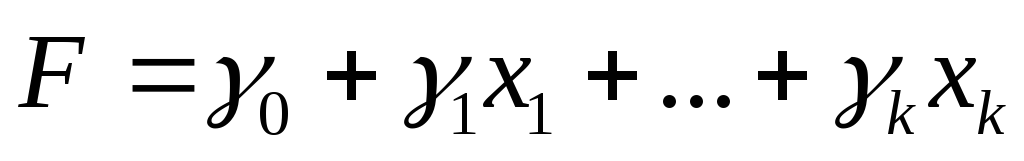
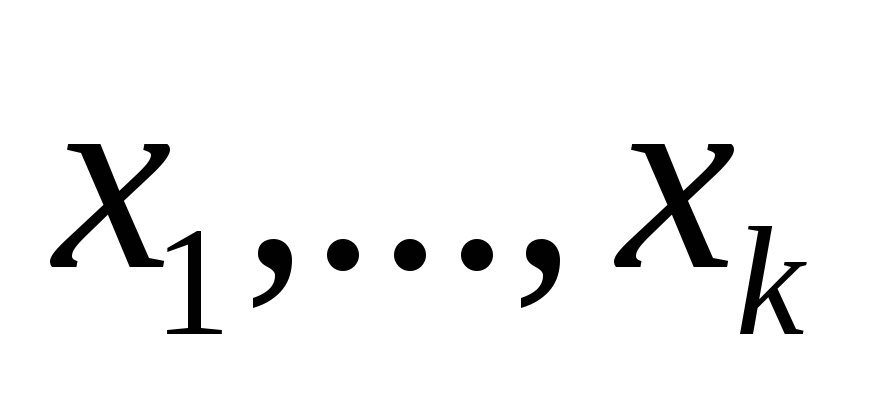
При решении основной задачи также учитывают ограничения относительно неизвестных 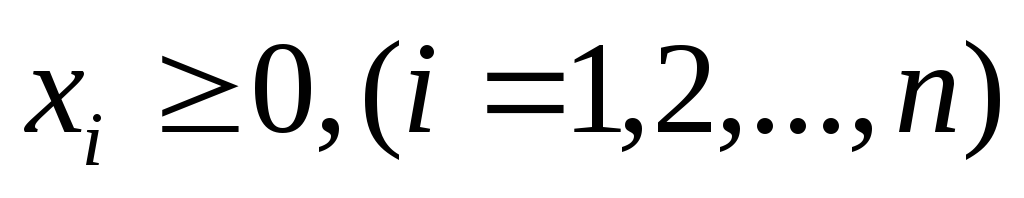. Учитывая равенства системы(**) для , получаем следующие неравенства:

Для свободных неизвестных также записываем ограничения и переходим к системе

содержащей n линейных неравенств относительно k неизвестных. Ясно, что каждому допустимому решению системы (**) отвечает решение получившейся системы неравенств. И наоборот, взяв произвольное решение системы неравенств и найдя по формулам системы(**) величины , получим неотрицательное решение системы (**), а значит, и системы основной задачи(*). Тем самым вместо того, чтобы искать неотрицательные решения системы (*), можно искать все решения системы неравенств.

В результате мы пришли к следующей математической задаче. Дана система неравенств, содержащая n линейных неравенств относительно неизвестных и линейная форма относительно тех же неизвестных. И требуется среди всех решений системы неравенств выбрать такое, при котором форма F достигает наименьшего значения. Такое решение также будет называться оптимальным.

Такую задачу называют основной задачей линейного программирования с ограничениями-неравенствами, либо задача формы А.

19. Линейное программирование. Геометрическое решение двумерных задач. Основная теорема о решении задачи лп.

Основная задача линейного программирования состоит в следующем. Задана система (6.10) m линейных алгебраических уравнений с n неизвестными x₁. x_n и линейная форма относительно этих же неизвестных: F = c₁x₁ + . + c_nx_n. (6.11) Условия в системе (10) могут быть заданы также в форме неравенств. Требуется среди всех неотрицательных решений системы (10) выбрать такое, при котором форма F принимает наименьшее значение (минимизируется). Определение: Система (6.10) называется системой ограничений данной задачи. Сами равенства (6.10) называются ограничениями-равенствами. Отметим, что кроме ограничений-равенств в основу задач входят также ограничения-неравенства x₁≥0. x_n≥0 Определение: Всякое неотрицательное решение x₁ (0) . x_n (0) (x_i (0) ≥0; i=1. n) системы (6.10) назовем допустимым. Допустимое решение часто называют планом задачи линейного программирования.

Геометрическое решение двумерных задач

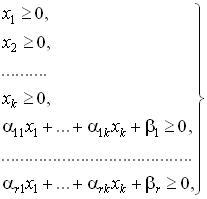
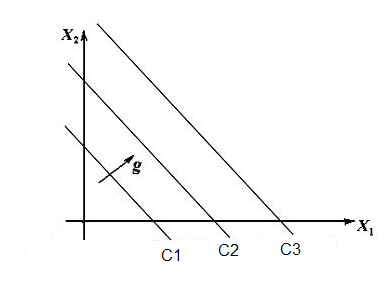
Геометрический смысл основной задачи линейного программирования становится предельно прозрачным, если перейти от нее к эквивалентной ей задаче с ограничениями-неравенствами, то есть к задаче (А): Дана система содержащая n= k = r линейных неравенств относительно k неизвестных x₁. x_k, и линейная форма относительно тех же неизвестных. Требуется среди всех решений системы выбрать такое, которое минимизирует форму F.

Будем рассматривать двумерный случай, то есть в системе и линейной форме присутствуют только x1 и x2. Введем на плоскости прямоугольную декартову систему координат x₁Ox₂. Известно, что геометрическое место точек на плоскости, координаты которых удовлетворяют системе линейных неравенств, образует выпуклый многоугольник. Этот многоугольник называется многоугольником решений данной системы неравенств. Стороны этого многоугольника располагаются на прямых, уравнения которых получаются, если в неравенствах системы знаки неравенств заменить точными равенствами. Сам же этот многоугольник есть пересечение полуплоскостей, на которые делит плоскость каждая из указанных прямых.

То есть для каждого неравенства строим прямую (уравнение прямо получаем из неравенства простой заменой знака сравнения на знак равенства). Неравенству будет удовлетворять одна из образовавшихся полуплоскостей, выделим её.

Проделав то же самое для всех условий из системы, получим многоугольник решений.

Далее рассмотрим линейную форму, запишем её в следующем виде:

Меняя значение С, получаем различные прямые, однако все они параллельны между собой, то есть образуют семейство параллельных прямых. Очевидно, что через каждую точку плоскости проходит одна прямая этого семейства. Каждую из прямых семейства принято называть линией уровня (линией различных значений) формы. При переходе от одной прямой к другой значение формы изменяется.

С1 > С2 > С3 Вектор g показывает направление уменьшения линейной формы, что для нашей задачи является нужным направлением. Задача теперь сводится к тому, чтобы найти линию с минимальным С в рамках найденной области. То есть будем сдвигать линию линейной формы по направлению g, пока линия еще находится в допустимой области. В нашем случае процесс остановится, когда линия будет проходить через точку Q, так как при дальнейшем смещении линии выйдет из приемлемой области. Получаем, что решением будет значения x1 и x2 в точке Q.

Основная теорема линейного программирования. Целевая функция задачи линейного программирования достигает своего экстремума (минимума или максимума) в вершине допустимой области. Если целевая функция достигает экстремального значения более, чем на одной вершине, то она достигает того же значения в любой точке, являющейся выпуклой комбинацией этих вершин.

Выпуклая комбинация – линейная комбинация с неотрицательными коэффициентами.

Источник