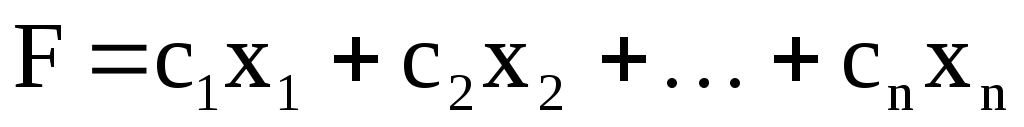2. Постановка задачи лп. Различные формы задач лп и их эквивалентность
Математические модели различных по содержательному смыслу экономических задач, рассмотренных выше, имеют много общего. Во всех примерах соответствующая математическая задача может быть сформулирована следующим образом: Максимизировать или минимизировать заданную линейную функцию нескольких переменных при заданных линейных ограничениях на переменные.
Это и есть постановка задачи ЛП в самом общем виде. При этом под линейным ограничением понимается любое линейное уравнение или линейное неравенство.
Функция, которую требуется максимизировать (минимизировать), называется
целевой функцией задачи.
Любой набор значений всех переменных задачи ЛП называется планом задачи. План, удовлетворяющий всем ограничениям задачи, называется допустимым. Допустимый план, на котором достигается наибольшее (наименьшее) среди всех допустимых планов значение целевой функции, называется оптимальным.
Решить задачу ЛП – это значит найти ее оптимальный план 
и соответствующее значение целевой функции
или доказать, что оптимальных планов нет.
Задачу ЛП в общей постановке всегда можно свести к любой из двух следующих форм (частных случаев общей задачи ЛП).
Стандартная задача ЛП:
(14)
(15)
. (16)
Каноническая задача ЛП:
(17)
(18)
(19)
Эти две формы задачи ЛП удовлетворяют следующим условиям:
1. В качестве направления оптимизации в них выбрана максимизация целевой функции.
2. В ограничениях присутствуют требования неотрицательности (16) и (19) для всех переменных задачи.
3. Все остальные ограничения, кроме требования неотрицательности всех переменных, однотипны: линейные неравенства (15) – в стандартной задаче, линейные равенства (18) – в канонической.
Замечание. Любое неравенство со знаком 
можно преобразовать в эквивалентное ему неравенство со знаком
, умножая обе части неравенства на множитель (-1). Поэтому без ограничения общности можно считать, что все неравенства в ограничениях задачи ЛП имеют знак
(или, наоборот, все неравенства имеют знак
).
Чтобы добиться выполнения условия 1 задачу минимизации целевой функции заменяют на задачумаксимизации функции
при тех же ограничениях на переменные. Легко проверяется (проделайте это самостоятельно), что оптимальные планы преобразованной задачи совпадают с оптимальными планами исходной и при этом 
Выполнение условия 2 достигается следующим образом: в целевую функцию и все ограничения задачи вместо каждой переменной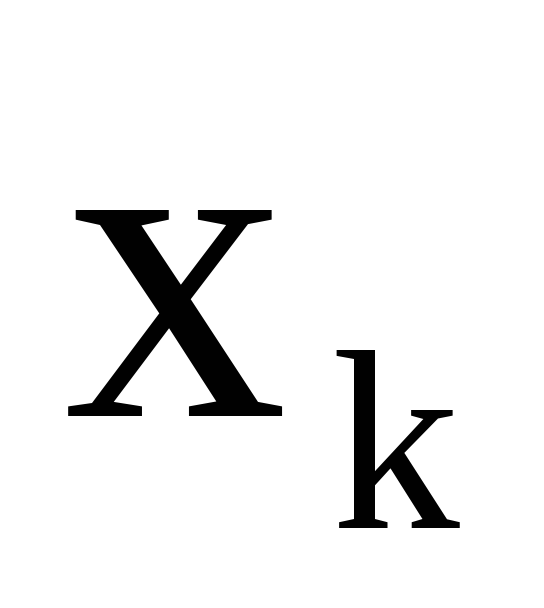 
произвольного знака (т. е. такой, что требование неотрицательности
отсутствует среди ограничений) подставляется выражение
для всех вновь введенных переменных в ограничения вводятся требования неотрицательности
Смысл такой замены очевиден: число произвольного знака можно представить в виде разности двух неотрицательных чисел. Ясно, что оптимальные значения
переменных исходной задачи находятся по формулам
где
— оптимальные значения переменных преобразованной задачи.
После выполнения двух описанных выше преобразований задача ЛП общего вида сведется к задаче максимизации с требованием неотрицательности всех ее переменных; среди остальных ограничений задачи могут встречаться как равенства, так и неравенства. Чтобы свести такую задачу ЛП к стандартной форме, надо исключить все ограничения – равенства; для сведения к канонической форме – заменить систему ограничений – неравенств на эквивалентную систему ограничений, записанную в виде равенств и требований неотрицательности некоторых (дополнительно введенных) переменных.
При исключении ограничений –равенств используются известные методы линейной алгебры. Если все ограничения-равенства образуют несовместную систему линейных уравнений, то задача ЛП не имеет допустимых и тем более оптимальных планов. Если эта система совместна и имеет ранг r, то с помощью метода Гаусса некоторые переменных задачи можно выразить через остальные. Подстановка этих выражений в целевую функцию и все ограничения-неравенства (включая и требования неотрицательности переменных) сводит задачу кстандартной форме; при этом число переменных уменьшается на r.
Для приведения задачи ЛП к канонической форме вводятся дополнительные, так называемые балансовые, переменные; число таких переменных равно числу ограничений-неравенств (без учета требований неотрицательности переменных) исходной задачи. Каждое ограничение – неравенство 
заменяется на эквивалентную ему пару ограничений
В случае неравенства со знаком 
балансовая переменная
включается вcоответствующее равенство со знаком минус.
Рассмотрим примеры применения описанных выше преобразований формы задач ЛП.
Пример 4. Привести к стандартной форме задачу ЛП
Решение. Решаем методом Гаусса систему ограничений-равенств
~ 
~
~ 
.
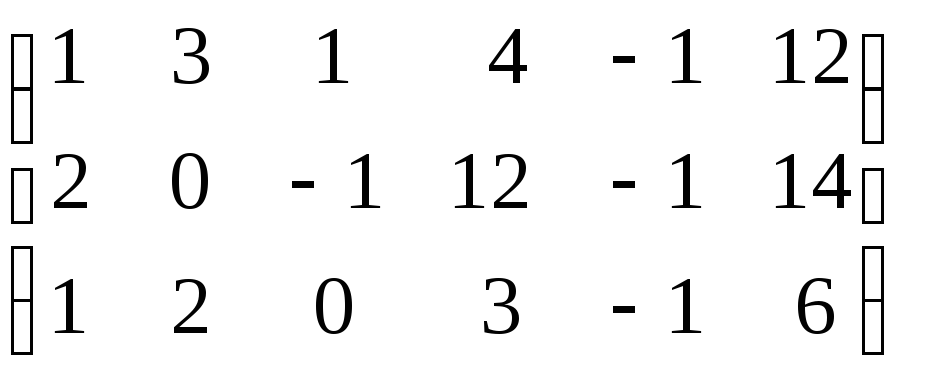
Из полученной трапециевидной формы системы последовательно выражаем 
через
(обратный ход метода Гаусса):
Подставим полученные выражения в целевую функцию и ограничения-неравенства; одновременно заменим задачу минимизации F на максимизацию
Глава 1. Линейное программирование
§1. Общая постановка задачи линейного программирования
Линейное программирование – раздел прикладной математики, занимающийся методами исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции многих переменных, на независимые переменные которых наложены линейные ограничения.
Такая линейная функция называется целевой, а набор количественных соотношений между переменными, выражающих определенные требования экономической задачи в виде уравнений или неравенств, называется системой ограничений. Совокупность соотношений, содержащих целевую функцию и ограничения на ее аргументы, называется математической моделью экономической задачи оптимизации. Слово «программирование» введено в связи с тем, что неизвестные переменные, которые находятся в процессе решения задачи, обычно определяют программу (план) работы некоторого экономического субъекта.
К задачам линейного программирования приводят исследования производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.
Задача линейного программирования (ЗЛП) ставится следующим образом: найти экстремум (максимум или минимум) линейной целевой функции
при линейных ограничениях:
где , , ( , ) – известные величины, ( ) – управляющие переменные. Формулы (1.1) – (1.3) представляют собой запись задачи линейного программирования в развернутом (координатном) виде.
Матричная запись ЗЛП имеет вид:
где – вектор-столбец коэффициентов целевой функции, – вектор управляющих переменных, – вектор-столбец свободных членов, – матрица коэффициентов при управляющих переменных (матрица условий).
Определение 1.1. Систему (1.2) называют системой функциональных, или ресурсных ограничений задачи линейного программирования.
Определение 1.2. Неравенства (1.3) называют прямыми ограничениями задачи линейного программирования.
Определение 1.3. Вектор , удовлетворяющий системе неравенств (1.2) – (1.3), называют допустимым решением или допустимым (опорным) планом задачи линейного программирования.
Определение 1.4. Допустимое решение , доставляющее целевой функции максимум или минимум, называют оптимальным решением, или оптимальным планом задачи линейного программирования.
Неравенства (1.2) – (1.3) определяют область допустимых решений задачи линейного программирования.
Формы записи злп, их эквивалентность и способы преобразования
Задачу линейного программирования можно записать в одной из приведенных ниже форм.
Симметрическая (стандартная) форма записи:
7 Общая постановка задачи линейного программирования формы записи злп
Задача линейного программирования (ЗЛП) в общем виде имеет три формы:
произвольную, симметричную и каноническую.
1. Произвольная форма задачи ЛП имеет вид:
Выражение называется целевой функцией задачи. Величины (Х1,Х2,…,ХN) – переменные задачи. Система неравенств в задаче (2) определяет область допустимых значений (планов) задачи D, которая имеет форму выпуклого многогранника. Неравенства и равенства в задаче (2) называются ограничениями. Каждое неравенство определяет полупространство, а равенство – плоскость в пространстве переменных.
Решение задачи (2) называется оптимальным решением (или оптимальным планом) и обозначается как Х*=(Х*1,Х*2,…,Х*N).
Если область D ограничена, то задача ЛП всегда имеет либо единственное, либо бесконечно много решений. Если решение единственно, то оно совпадает с одной из вершин многогранника D. Если градиент целевой функции c=(с1,с2,…,сn) коллинеарен градиенту одного из ограничений, то задача имеет бесконечно много решений, лежащих на данном ограничении.
Если ограничения несовместны, или целевая функция неограниченна в неограниченной области D, то задача (2) не имеет решения. Всякая задача на минимум может быть сведена к задаче на максимум и наоборот, умножением целевой функции на –1. Оптимальный план задачи при этом не изменится, а значение целевой функции изменит знак. После решения надо снова изменить знак значения целевой функции.
2. Симметричная форма ЗЛП имеет два вида.
Симметричная форма задачи на максимум:
Задача (3) обычно имеет следующий экономический смысл: это объемы производства го вида продукции, цены или прибыль на единицу продукции, затраты го вида ресурса на производство го вида продукции, имеющийся запас го вида ресурса. Задача (3) ставится на определение такого плана производства продукции, который дает максимальную выручку или прибыль, при заданных ограничениях на имеющиеся ресурсы.
3. Каноническая форма задачи ЛП.
Определение. Если в ограничениях (5) есть переменные, отсутствующие в других ограничениях и с коэффициентами равными единице, то они называются базисными, остальные переменные называются свободными.
Каноническая форма с базисными переменными является исходной для решения задачи симплекс алгоритмом.
Для изготовления р1 ир2, используется ресурсы S1, S2. Запасы ресурсов число единиц затраченных на изготовление единицы продукции
Количество единиц затраченных на изготовление единицы продукции