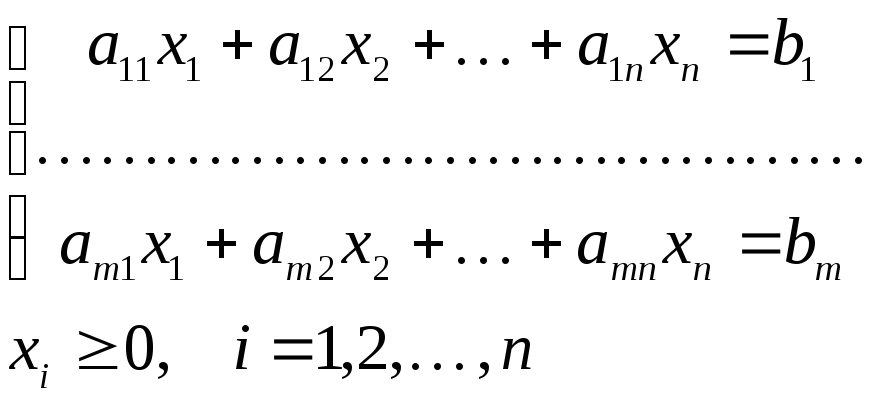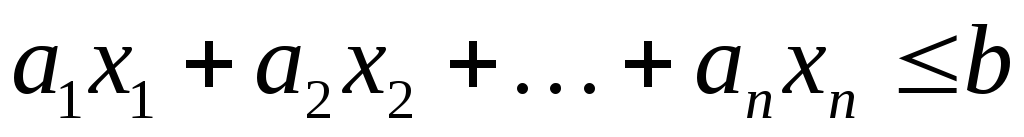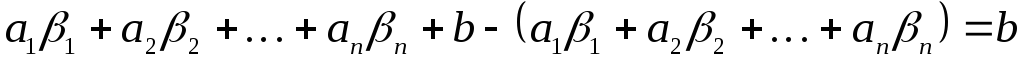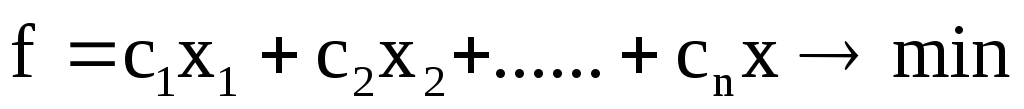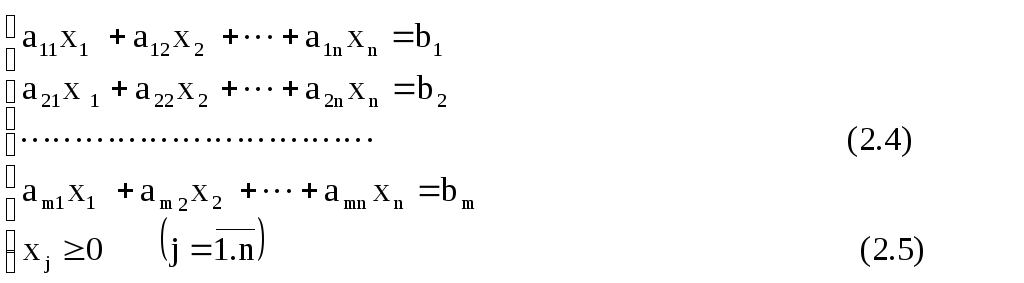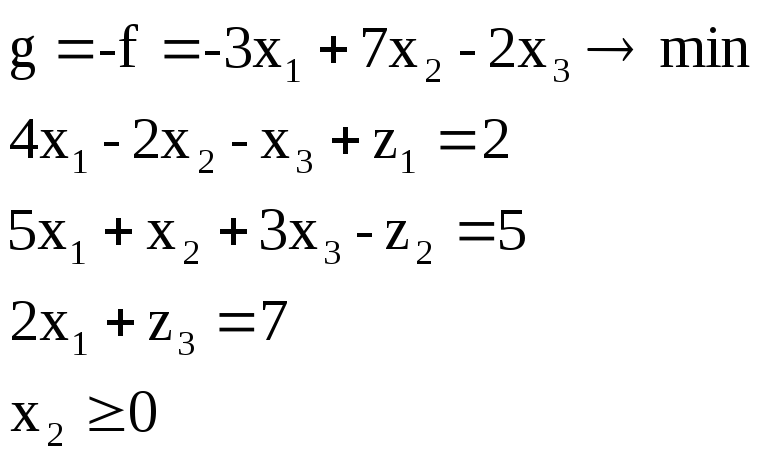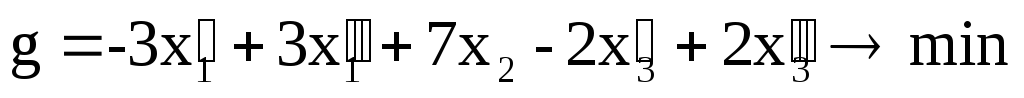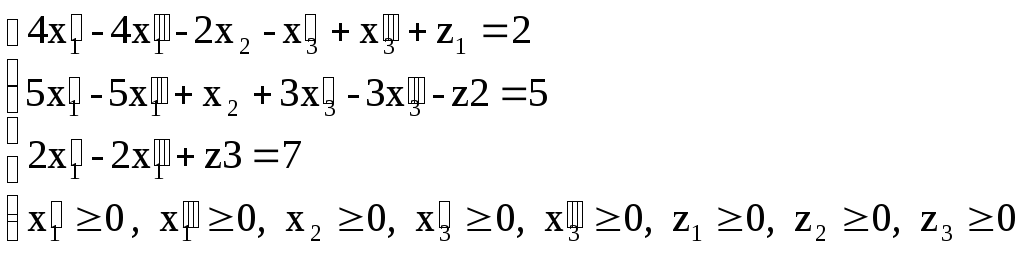Задача линейного программирования имеет канонический вид

Переход к канонической форме ЗЛП

Каноническая форма ЗЛП — задача линейного программирования вида ax = b , где a — матрица коэффициентов, b — вектор ограничений.

Инструкция . Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word .

Математическая модель ЗЛП называется основной, если ограничения в ней представлены в виде уравнений при условии неотрицательности переменных.

Математическая модель называется канонической, если ее система ограничений представлена в виде системы m линейно независимых уравнений (ранг системы r=m), в системе выделен единичный базис, определены свободные переменные и целевая функция выражена через свободные переменные. При этом правые части уравнений неотрицательны (b_i ≥ 0).

Переменные, входящие в одно из уравнений системы с коэффициентом один и отсутствующие в других уравнениях называются базисными неизвестными, а все другие – свободными.

Решение системы называется базисным, если в нем свободные переменные равны 0, и оно имеет вид:
X_баз = (0, 0; b₁, …, b_m), f(X_баз) = c₀

Базисное решение является угловой точкой множества решений системы, т.е. определяет вершину многоугольника решений модели. Среди таких решений находится и то, при котором целевая функция принимает оптимальное значение.

Базисное решение называется опорным, если оно допустимо, т.е. все правые части уравнений системы (или неравенств) положительны b_i ≥ 0.

Компактная форма канонической модели имеет вид:
AX = b
X ≥ 0
Z = CX(max)

Понятие допустимого решения, области допустимых решений, оптимального решения задачи линейного программирования.
Определение 1 . Вектор X, удовлетворяющий системе ограничений ЗЛП, в том числе и условиям неотрицательности, если они имеются, называется допустимым решением ЗЛП.
Определение 2 . Совокупность всех допустимых решений образует область допустимых решений (ОДР) ЗЛП.
Определение 3 . Допустимое решение, для которого целевая функция достигает максимума (или минимума), называется оптимальным решением.

• эти значения удовлетворяли некоторой системе линейных уравнений или неравенств;
• при этих значениях целевая функция обращалась бы в минимум или максимум.

• неравенства, входящие в систему ограничений задачи, преобразовать в уравнения с помощью введения дополнительных переменных;
• если целевая функция F→max (максимизируется), она заменяется на функцию –F→ min (которая минимизируется).

Пример №1 . Следующую задачу ЛП привести к каноническому виду: F(X) = 5x₁ + 3x₂ → max при ограничениях:
2x₁ + 3x₂≤20
3x₁ + x₂≤15
4x₁≤16
3x₂≤12
Модель записана в стандартной форме. Введем балансовые неотрицательные переменные x₃, x₄, x₅, x₆, которые прибавим к левым частям ограничений-неравенств. В целевую функцию все дополнительные переменные введем с коэффициентами, равными нулю:
В первом неравенстве смысла (≤) вводим базисную переменную x₃. Во 2-ом неравенстве смысла (≤) вводим базисную переменную x₄. В третьем неравенстве вводим базисную переменную x₅. В 4-м неравенстве — базисную переменную x₆. Получим каноническую форму модели:
2x₁ + 3x₂ + 1x₃ + 0x₄ + 0x₅ + 0x₆ = 20
3x₁ + 1x₂ + 0x₃ + 1x₄ + 0x₅ + 0x₆ = 15
4x₁ + 0x₂ + 0x₃ + 0x₄ + 1x₅ + 0x₆ = 16
0x₁ + 3x₂ + 0x₃ + 0x₄ + 0x₅ + 1x₆ = 12
F(X) = 5x₁ + 3x₂ + 0x₃ + 0x₄ + 0x₅ + 0x₆ → max Пример №2 . Найти два опорных решения системы
x₁ + 2x₄ – 2x₅ = 4
x₃ + 3x₄ + x₅ = 5
x₂ + 3x₅ = 2 Ответ: X = (4;2;5;0;0) Пример №3 . Привести к канонической форме следующую ЗЛП.
F = 2x₁ — x₂ + 4x₃ -2x₄ → min
при ограничениях:
7x₁ –x₂ +5x₃ + x₄ = -10
3x₁ +5x₂ -9x₃ + 2x₄ = 6
x₁ –x₂ -2x₃ + 6x₄ ≥ 7
x₁ +x₂ -5x₃ ≤ 11
7x₁ –x₂ -3x₃ — x₄ ≤ 9
x₁ ≥0 , x₂ ≥0 (обратите внимание, что переменные x₃ и x₄ имеют произвольный знак) Для приведения ЗЛП к канонической форме необходимо:
1. Поменять знак у целевой функции
— F = -2x₁ + x₂ — 4x₃ +2x₄ → max 2. В левые части трех последних неравенств внести дополнительные переменные x₅, x₆, x₇ со знаком плюс или минус в зависимости от знака неравенства.
7x₁ –x₂ +5x₃ + x₄ = -10
3x₁ +5x₂ -9x₃ + 2x₄ = 6
x₁ –x₂ -2x₃ + 6x₄ –x₅ = 7
x₁ +x₂ -5x₃ +x₆ = 11
7x₁ –x₂ -3x₃ — x₄ +x₇ = 9
x₁ ≥0 , x₂ ≥0, x₅ ≥0 , x₆ ≥0, x₇ ≥0 3. Так как переменные x₃ и x₄ произвольного знака, то они заменяются разностями неотрицательных переменных.
7x₁ –x₂ +5(x₈ – x₉) + (x₁₀ – x₁₁) = -10
3x₁ +5x₂ -9(x₈ – x₉) + 2(x₁₀ – x₁₁) = 6
x₁ –x₂ -2(x₈ – x₉) + 6(x₁₀ – x₁₁) –x₅ = 7
x₁ +x₂ -5(x₈ – x₉) +x₆ = 11
7x₁ –x₂ -3(x₈ – x₉) — (x₁₀ – x₁₁) +x₇ = 9
x₁ ≥0 , x₂ ≥0, x₅ ≥0 , x₆ ≥0, x₇ ≥0 , x₈ ≥0, x₉ ≥0 , x₁₀ ≥0, x₁₁ ≥0 4. Соответствующая целевая функция примет вид:
— F = -2x₁ + x₂ — 4(x₈ – x₉) +2(x₁₀ – x₁₁) → max см. также Как привести каноническую задачу линейного программирования к стандартной форме Пример №2 . Преобразовать следующие задачи ЛП к канонической форме и решить их симплекс-методом.

Источник

Задача линейного программирования

В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися. В случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической. Каноническая задача линейного программирования в координатной форме записи имеет вид:

Используя знак суммирования эту задачу можно записать следующим образом:

Каноническая задача линейного программирования в векторной форме имеет вид:

В данном случае введены векторы:

,

,,

Здесь – скалярное произведение векторови.

Каноническая задача линейного программирования в матричной форме записи имеет вид:

,.

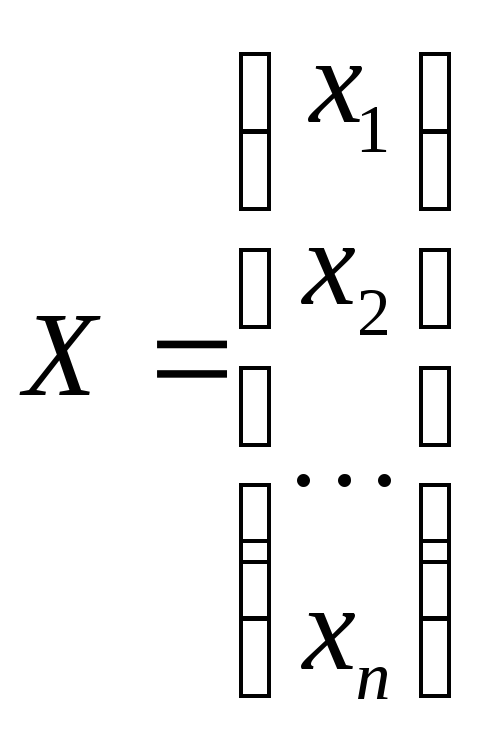
Здесь – матрица коэффициентов системы уравнений,– матрица-столбец переменных задачи;– матрица-столбец правых частей системы ограничений.

Нередко используются задачи линейного программирования, называемые симметричными, которые в матричной форме записи имеют вид:

или

Приведение общей задачи линейного программирования к канонической форме

В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако, при составлении математических моделей экономических задач ограничения в основном формулируются системы неравенств, поэтому возникает необходимость перехода от системы неравенств к системе уравнений. Это может быть сделано следующим образом. К левой части линейного неравенства:

прибавляется величина , такая, что переводит неравенство в равенство, где:

.

Неотрицательная переменная называетсядополнительнойпеременной.

Основания для возможности такого преобразования дает следующая теорема.

Теорема.Каждому решению неравенства

соответствует единственное решение уравнения:

и неравенства , и, наоборот, каждому решениюуравнения:

и неравенства соответствует единственное решениенеравенства:

.

Доказательство.Пусть– решение неравенства. Тогда:

или

Если в уравнение вместо переменных подставить значения=, получится:

Таким образом, решение удовлетворяет уравнению:

и неравенству.

Доказана первая часть теоремы.

Пусть удовлетворяет уравнениюи неравенству, т.е.и. Отбрасывая в левой части равенства неотрицательную величину, получим:

_,

т.е. удовлетворяет неравенству:

_,

что и требовалось доказать.

Если в левую часть неравенств системы ограничений вида ,добавить переменную,, то получится система ограничений – уравнений,. В случае, если система неравенств–ограничений имеет вид,, то из левой части неравенств–ограничений нужно вычесть соответствующую неотрицательную дополнительную переменную,.

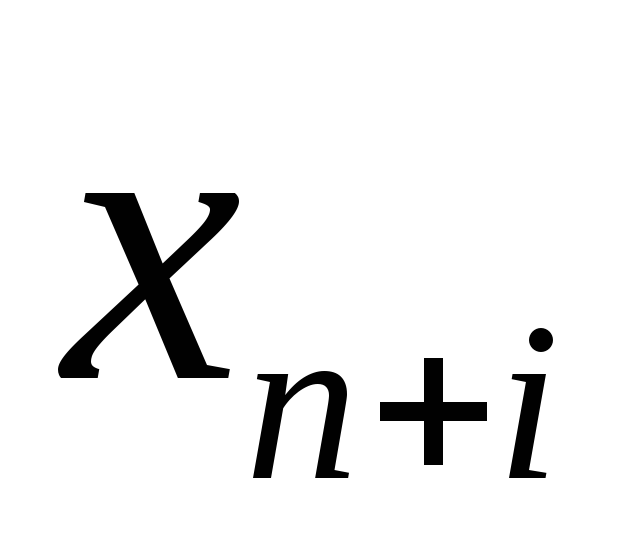
Полученная таким образом система уравнений–ограничений, вместе с условиями неотрицательности переменных, т.е. 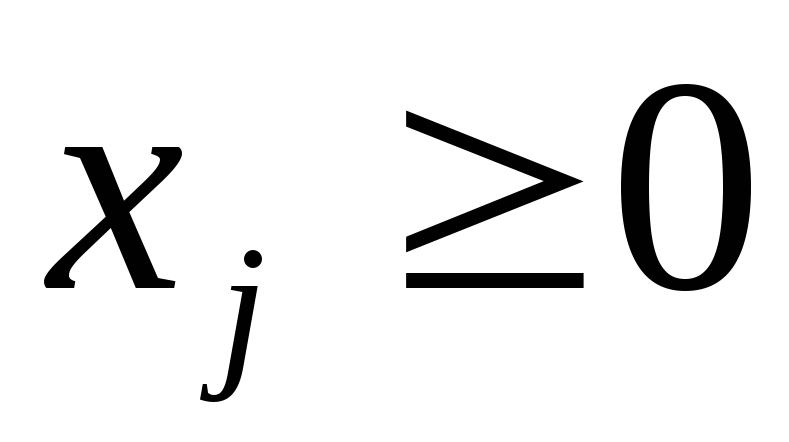,и целевой функцией является канонической формой записи задачи линейного программирования.

Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому не влияют на ее значения.

В реальных практических задачах дополнительные неизвестные имеют определенный смысл. Например, если левая часть ограничений задачи отражает расход ресурсов на производство продукции в объемах ,, а правые части — наличие производственных ресурсов, то числовые значения дополнительных неизвестных,означают объем неиспользованных ресурсов-го вида.

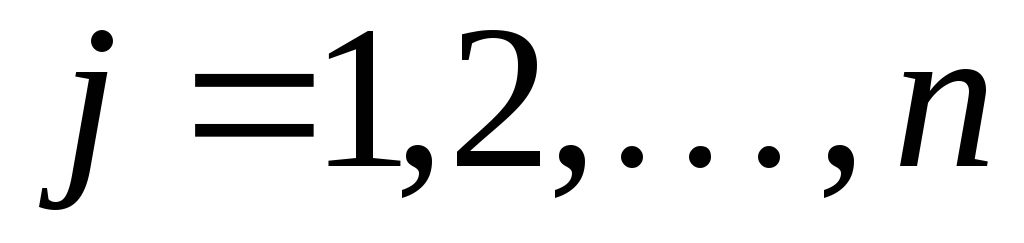
Иногда возникает также необходимость перейти в задаче от нахождения минимума к нахождению максимума или наоборот. Для этого достаточно изменить знаки всех коэффициентов целевой функции на противоположные, а в остальном задачу оставить без изменения. Оптимальные решения полученных таким образом задач на максимум и минимум совпадают, а значения целевых функций при оптимальных решениях отличаются только знаком.

Источник

2.6. Канонический вид злп.

В исходной постановке ЗЛП могут допускать различные формы записи. Так, в одних задачах требуется максимизировать целевую функцию, в других — минимизировать; некоторые линейные ограничения могут иметь вид равенств, другие — неравенств и т.д.

Для единообразия записи ЗЛП вводится так называемая каноническая форма записи.

Говорят, что ЗЛП записана в канонической форме, если она имеет следующий вид:

(2.3)

Отметим следующие особенности канонического вида:

1) требуется минимизировать целевую функцию;

2) все линейные ограничения, кроме требований неотрицательности переменных, имеют вид равенств;

1. на все переменные наложены требования неотрицательности.

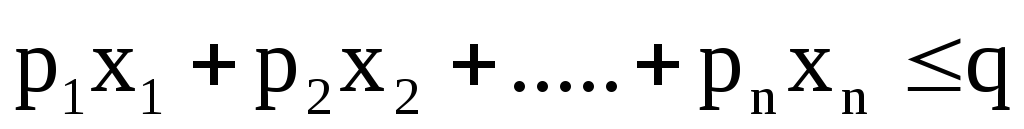
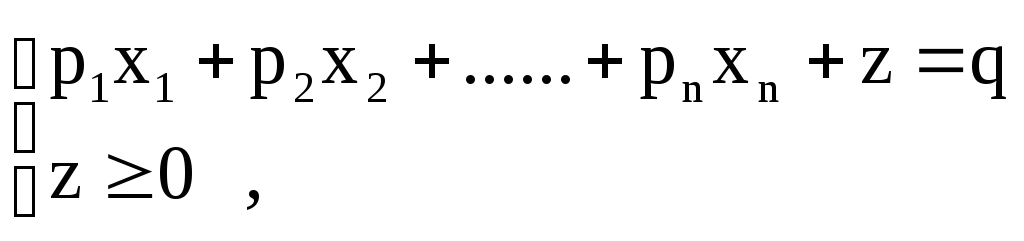
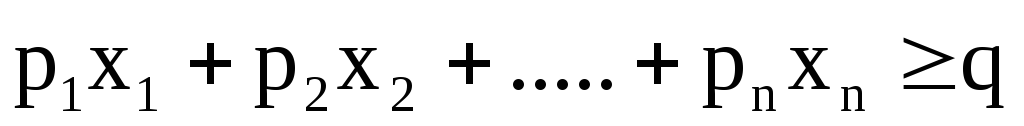
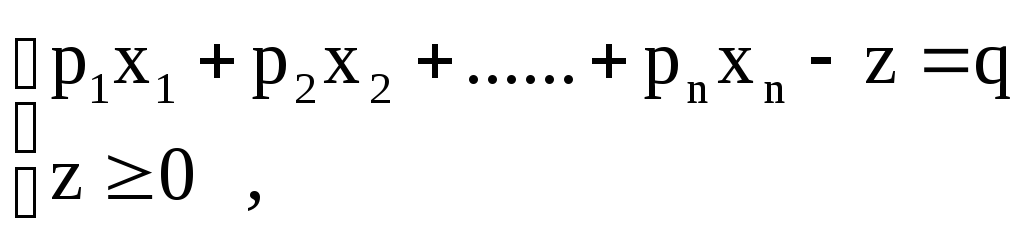
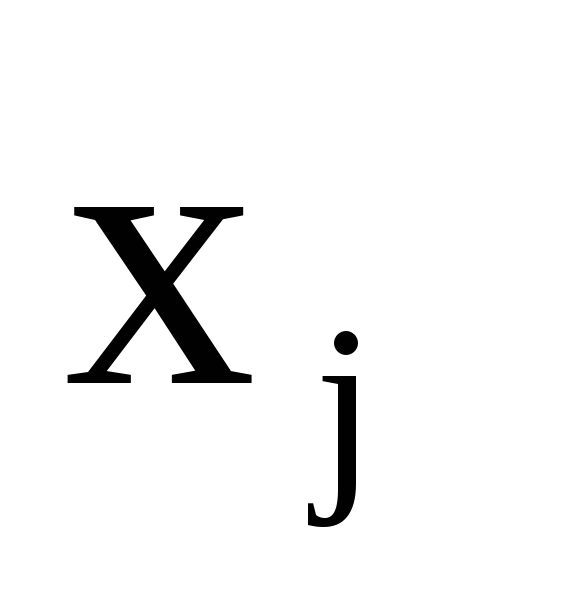
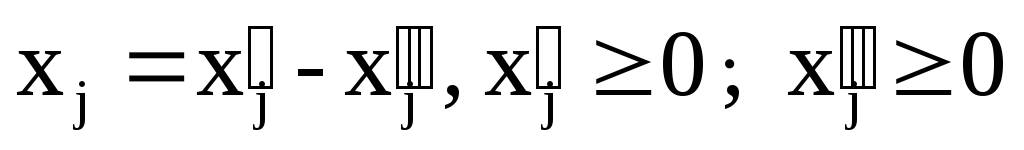
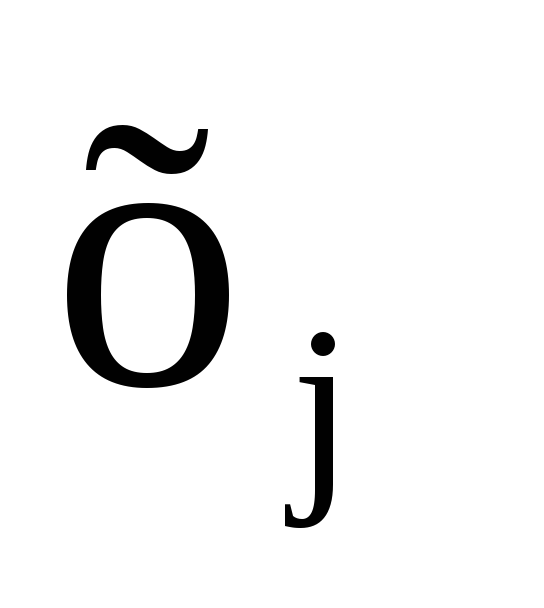
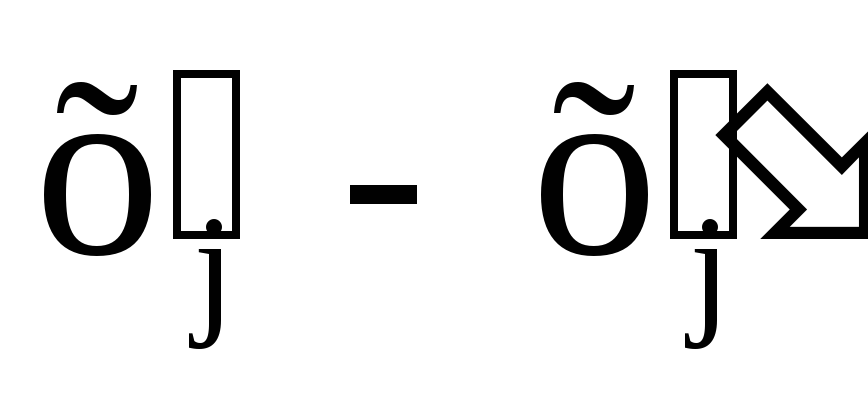
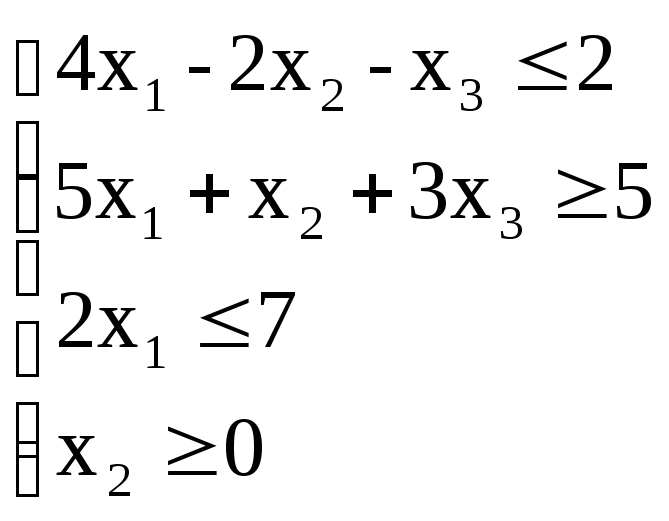
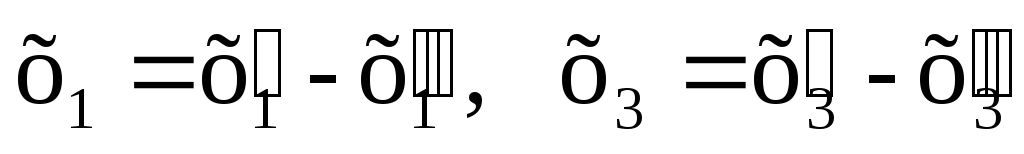
Покажем, что любую ЗЛП можно привести к каноническому виду. 1) Если в ЗЛП требуется максимизировать целевую функцию f, то положим g = — f и потребуем минимизировать функцию g. Получится новая ЗЛП, которая эквивалентна исходной в том смысле, что каждое оптимальное решение исходной задачи будет оптимальным решением новой задачи и наоборот. 2) Предположим, что в ЗЛП есть линейное ограничение вида . Заменим такое ограничение следующими двумя ограничениями: где z— новая переменная, которая в целевую функцию вводится с коэффициентом 0 (иначе говоря, переменная z не вводится в целевую функцию). Значение переменной z можно не учитывать после решения новой задачи. Аналогично, ограничение вида заменяется двумя ограничениями: 3) Предположим, что в ЗЛП не ко всем переменным предъявлено требование неотрицательности. Тогда каждую, переменную , на которую не наложено требование неотрицательности, представим в виде разности двух неотрицательных переменных: (2.6) Каждое вхождение переменной в целевую функцию или ограничения заменим разностью. Решив новую задачу с помощью (2.6), вернемся к прежним переменным. Указанными приемами любая ЗЛП приводится к каноническому виду. Пример. Привести к каноническому виду Проделаем описанные действия. Теперь получим ЗЛП в каноническом виде:

2.7. Понятие опорного плана злп.

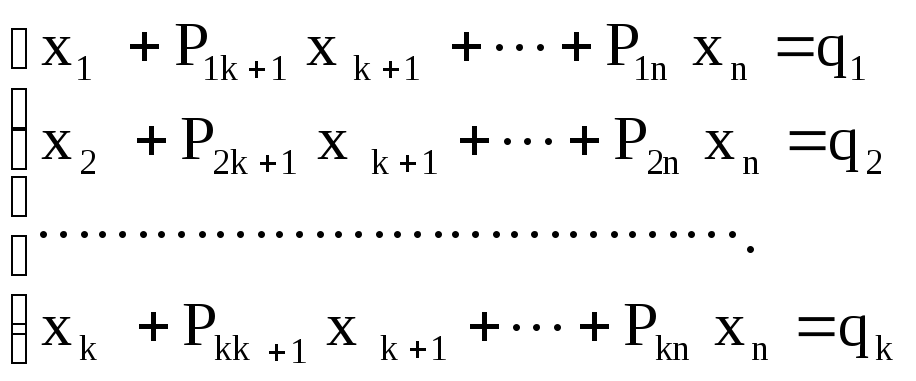
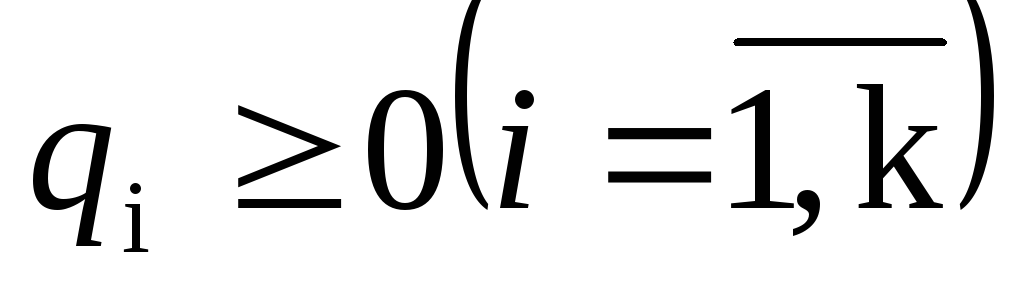
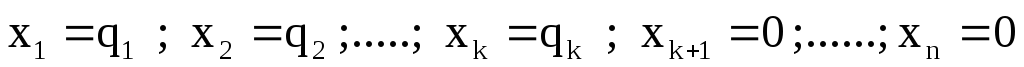
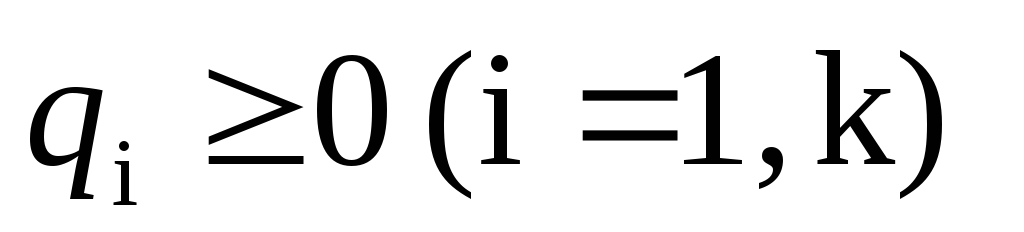
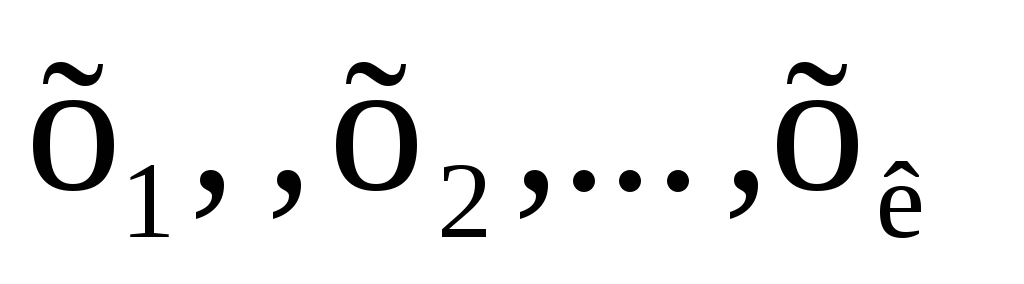
Пусть ВЛП задана в каноническом виде (2.3 — 2.5). Предположим, что система уравнений (2.4) приведена к жордановой форме с неотрицательными правыми частями: (2.6) где . Приравняв к нулю свободные переменные, получим базисное решение системы (2.4) (2.7) В силу условия набор значений переменных (2.7) удовлетворяет и ограничениям (2.5). Поэтому (2.6) являетсядопустимым решением ЗЛП. Допустимое решение (2.7) называется базисным допустимым решением или опорным планом ЗЛП. При этом говорят, что переменные образуют допустимый базис. Оказывается, что если ОДР изобразить геометрически, то каждый опорный план ЗЛП соответствует вершине многогранника. Поэтому справедлива следующая теорема. Если ЗЛП разрешима, то существует оптимальный опорный план.

3. Симплексный метод решения злп

3.1. Общая характеристика и основные этапы симплекс – метода

Основоположниками симплекс-метода являются советский математик Л.В. Канторович и американский математик Дж. Данциг. Симплекс-методом можно решить любую ЗЛП или обнаружить ее неразрешимость. Многие специальные классы ЗЛП можно решить другими, более эффективными для этих классов методами. Однако преимущество симплекс-метода — его универсальность. Почти для всех ЭВМ разработаны стандартные программы для решения ЗЛП симплекс — методом. Опишем общую идею симплекс-метода. Считаем, что ЗЛП записана в каноническом виде и целевую функцию нужно минимизировать. Как мы уже знаем, оптимальный план следует искать среди опорных планов ЗЛП. Симплекс-метод не перебирает все опорные планы (что было бы часто невозможно из-за их огромного количества), а, начиная с некоторого исходного опорного плана, он последовательно переходит к другим опорным планам с уменьшением целевой функции. Симплекс-метод прекращает свою работу тогда, когда либо будет найден оптимальный опорный план, либо установлена неразрешимость задачи. При решении ЗЛП симплекс-методом можно выделить следующие этапы: 1) приведение ЗЛП к каноническому виду; 2) приведение системы линейных уравнений к жордановой форме с неотрицательными правыми частями с одновременной проверкой на неразрешимость ЗЛП из-за противоречивости системы линейных ограничений; 3) исследование опорного плана на оптимальность; 4) исследование ЗЛП на неразрешимость из-за неограниченности снизу на ОДР целевой функции; 5) переход к новому, «лучшему» опорному плану.

Источник