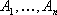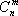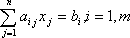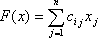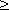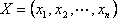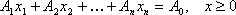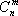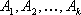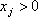Задача линейного программирования имеет единственное решение

1.2. Свойства решений задач линейного программирования

где — произвольные неотрицательные числа, удовлетворяющие условию .

Множество точек линейного пространства называется выпуклым, если вместе с любыми двумя своими точками оно содержит и их произвольную линейную комбинацию.

Любая точка х выпуклого множества называется угловой, если она не может быть представлена в виде линейной комбинации каких-либо двух других различных точек данного множества.

Многогранником решений задачи линейного программирования называется множество планов (непустое) задачи линейного программирования. Вершиной называется всякая угловая точка многогранника.

Допустимые планы задачи линейного программирования считаются базисными, если в многограннике решений им соответствуют угловые (крайние) точки.

Базисные планы с неотрицательными компонентами называются опорными

Теорема 1.1. Множество планов основной задачи линейного программирования является выпуклым (если не является пустым).

Теорема 1.2. Если задача линейного программирования имеет оптимальное решение (в ограниченной области всегда, а в неограниченной – в зависимости от условий, наложенных на функцию ), то оно совпадает, по крайней мере, с одним из опорных решений системы ограничительных уравнений.

Теорема 1.3. 1. Целевая функция f задачи линейного программирования достигает своего экстремального значения в вершине многогранника области допустимых решений (единственное решение).

2. Если линейная функция принимает экстремальное значение более чем в одной вершине, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих вершин (бесконечное множество решений).

Задачи линейного программирования на минимум и на максимум могут быть преобразованы к одному виду задач, например на максимум. Так как справедливо соотношение , то для отыскания минимума целевой функции

можно перейти к нахождению максимума функции

Графический метод решения задач линейного программирования Случай двух переменных

Постановка задачи в этом случае имеет вид:

Каждое из ограничительных неравенств области решений определяет полуплоскость с граничными прямыми

Если рассматривается система неравенств, то областью её решений может быть один из следующих случаев. 1) Система несовместна, когда область решений является пустым множеством.

2) Система неравенств совместна, то есть, область её решений выпуклое непустое множество, называемое многоугольником решений (в отличие от «многогранника решений», когда число неизвестных ), либо выпуклая многогранная область, уходящая в бесконечность.

Если система является совместной, то сторонами многоугольника решений являются прямые, которые получаются при замене знаков неравенств в ограничениях на знаки равенств.

Для определения экстремума ограниченной сверху целевой функции необходимо для случая:

1. Если , построить линию уровня (h –некоторая постоянная), таким образом, чтобы она проходила через многоугольник решений. При выполнении условия (то есть, проходит через начало координат) линия называется опорной. Построить вектор – градиент целевой функции . Передвигать линию уровня параллельно самой себе в направлении градиента, до тех пор, пока не будет достигнута последняя точка многоугольника решений (Рис.1.1). Координаты соответствующей точки дадут оптимальный план решений. Координаты точки можно уточнить аналитически, решая систему уравнений для прямых, которые пересекаются в данной точке.

2. Если , то линия уровня передвигается в направлении, противоположном своему градиенту (в направлении антиградиента) до достижения крайней точки многоугольника решений (Рис.1.2).

При решении могут встретиться следующие случаи.

1. Целевая функция F принимает максимальное значение в единственной точке А рис.1.1 (единственное решение).
2. Целевая функция принимает минимальное значение в точке В рис. 1.2 (единственное решение).
3. Целевая функция F принимает максимальное значение в любой точке прямой АВ рис 1.3. Прямая АВ перпендикулярна градиенту. (бесконечное множество решений).
4. Целевая функция не ограничена сверху на множестве допустимых решений Рис. 1.4. Максимум недостижим.
5. Система ограничений несовместна рис. 1.5. Решений нет.

Чтобы найти решение задачи линейного программирования геометрическим способом, необходимо:

а) построить прямые, которые получаются из ограничений заменой знаков неравенств на знаки равенства,

б) найти полуплоскости, определяемые каждым из ограничений.

а) построить прямую (линию уровня) , проходящую через область допустимых значений (иногда удобно строить опорную линию f = ),

б) передвигать линию уровня параллельно самой себе в направлении градиента (при отыскании максимума), либо в направлении антиградиента (при отыскании минимума), до точки, в которой целевая функция либо принимает максимальное (минимальное) значение, либо устанавливается её неограниченность,

в) определить координаты точки пересечения граничных прямых, в которой целевая функция принимает экстремальное значение.

Пример 3. Найти максимальное и минимальное значения функции

Решение. Строим координатную плоскость и наносим на неё прямые — ограничения (Рис.1.6). Первое уравнение неравенства можно преобразовать в равенство, уравнение границы или уравнение прямой (1) в отрезках и построить её, откладывая на соответствующих осях и отрезки 3 и 8. Если в неравенство (1) подставить координаты точки О(0;0), то неравенство будет , что неверно, отсюда следует, что области решений будет принадлежать полуплоскость со стороны, противоположной началу координат. Аналогичным образом преобразуем второе неравенство: и построим прямую (2). Области решений будет принадлежать полуплоскость с той стороны от прямой, где находится начало координат, так как при подстановке точки О(0;0) получим верное неравенство . Преобразуем третье неравенство: и построим прямую (3). Области решений будет принадлежать полуплоскость с той стороны от прямой, где находится начало координат, так как при подстановке точки О(0;0) получим верное неравенство . Таким образом, область решений задачи представляет собой треугольник АВD.

Для определения максимума целевой функции строим линию уровня , проходящую через область решений, и перпендикулярно к ней – вектор . В направлении этого вектора перемещаем линию уровня параллельно самой себе до точки А, которая является конечной точкой области решений. Эта точка, в которой целевая функция достигает максимума. Чтобы найти её координаты, решаем совместно второе и третье уравнения

Таким образом, максимальное значение целевой функции будет .

Чтобы найти минимальное значение целевой функции, линию уровня передвигаем влево, до конечной точки В. Получаем . Координаты точки В получаем, решая совместно первое и третье уравнения

Следовательно, минимальное значение целевой функции будет

Источник

Общая задача линейного программирования.

3) цель задачи ()

(max F(x))

(min F(x))

Определение: Планом или допустимым решением задачи линейного программирования называется вектор , удовлетворяющий условиям 1) и 2)

(*)

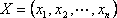
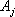
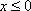
Определение: План называетсяопорным, если векторы , входящие в разложение (*) с положительными коэффициентами, являются линейно независимыми.

Определение: Опорный план называется невырожденным, если он содержит m – положительных компонентов, в противном случае опорный план называется вырожденным.

Определение: Оптимальным планом (решением) задачи линейного программирования называется план, доставляющий линейной форме наибольшее или наименьшее значение.

В большинстве задач ограничения задаются не в виде системы уравнений, а в виде системы линейных неравенств, либо система ограничений смешанная, однако любую систему ограничений можно привести к системе уравнений. Для этого достаточно к левой части каждого неравенства прибавить (для ) или отнять (для) какое-то неотрицательное число (добавочную переменную) с тем, чтобы каждое неравенство обратилось в уравнение, в результате получим эквивалентные системы уравнений и неравенств.

Основные теоремы линейного программирования

Теорема 1: Множество всех допустимых решений системы ограничений задачи линейного программирования, является выпуклым.

Теорема 2: Если существует, и при том единственное, оптимальное решение задачи линейного программирования, то оно совпадает с одной из угловых точек множества допустимых решений. Если линейная форма принимает минимальное (максимальное) значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.

Из теоремы 2 следует, что поиски оптимального решения можно ограничить перебором конечного числа угловых точек (их число меньше , гдеn — число неизвестных , а m – число ограничений), однако построение возможно только для двух и трёхмерных пространств, поэтому нужны аналитические методы, позволяющие находить координаты угловых точек.

Теорема 3: Если известно, что система векторов в разложении линейно независима и такова, что, где, то точкаявляется угловой точкой многогранника решений.

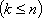
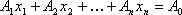
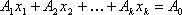
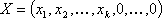
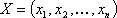
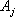
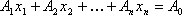
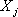
Теорема 4: Если — угловая точка многогранника решений, то векторыв разложении, соответствующие положительным, являются линейно независимыми.

Следствие 1: Так как векторы 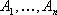имеют размерностьm, то угловая точка многогранника решений имеет не более m положительных компонент .

Следствие 2: Каждой угловой точке многогранника решений соответствует линейно независимых векторов системы векторов.

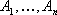
Симплексный метод решения задачи линейного программирования.

Доказано, что оптимальное решение задачи линейного программирования связано с угловыми точками многоугольника решений, то есть с опорными планами. Они определяются системой m — линейно независимых векторов, содержащихся в системе из n — векторов. Количество опорных планов меньше, гдеn — число неизвестных, а m – число ограничений. При больших n и m найти все их перебором очень трудно, поэтому необходимо упорядоченный перебор, такой схемой является симплексный метод, который позволяет исходя из известного опорного плана задачи, за конечное число шагов получить её оптимальный план. Каждый из шагов (итераций) состоит в нахождении нового плана, которому соответствует меньшее для задачи на минимум (большее для задачи на максимум) значение линейной формы, чем её значение в предыдущем плане. Процесс продолжается до получения оптимального плана. Если задача не обладает планами или её линейная форма неограниченна на многограннике решений, то симплексный метод позволяет установить это в процессе решения.

Источник