Линейное программирование в экономическом анализе
Основа выполнения любой задачи – это приятие кем-либо оптимального решения. Оптимальное решение позволяет достичь цель в заданных условиях с максимальным эффектом. Появление математических исследований конкретных проблем экономики приходится на конец 19-го- начало 20-го века.
К. Маркс описал в своей модели расширенного воспроизводства традиционное использование математических методов для формализованной характеристики. Данная модель стала первой макроэкономической моделью, которая позволяет открыть важные особенности производства.
Создатель математической школы Л. Вальрас в 1974 году разработал единую статистическую экономико-математическую модель народного хозяйства, которая стала называться системой общего равновесия экономики.
В модели Вальраса рациональными элементами являются постановка экстремальной задачи на экономики в целом и подход к стоимости как составляющей поиска общего оптимума.
В 1897 году известным буржуазным экономистом-математиком Парето на основе статистического материала была установлена закономерность распределения доходов в обществе в виде гиперболы – «кривая Парето».
В 1904 году русский экономист-математик В. К. Дмитриев создал уравнения связи расходов и выпуска продукции, использованные в дальнейшем американским экономистом В. Леонтьевым с целью построения баланса «затраты-выпуск».
Данные работы являются первыми попытками построить экономико-математическую модель. Их разработка разделила экономико-математический анализ статистических данных на два направления:
- Использование методов с целью характеристики экономических явлений;
- Для определения зависимости между ними.
В 1939 году ленинградским государственным университетом была выпущена книга Л.В. Канторовича «Математические методы организации и планирования производства». И лишь только через десять лет метод линейного программирования был переоткрыт в другой форме в США. Статьи по данной проблеме были опубликованы в 1949 году, в них Дж. Данциг излагал свой симплексный метод, который имеет много общих черт с методом последовательного преобразования плана, применявшимся Л. В. Канторовичем в решении практических задач.
Еще до Канторовича в России публиковались работы, содержавшие предпосылки к определению линейного программирования. Например, в 1930 году экономисты-транспортники, чтобы построить оптимальный план перевозок, разработали транспортную задачу в сетевом виде и решили ее без использования математического обоснования.
Работы по линейному программированию стали часто издаваться в 1950-х годах, когда велась детальная разработка основных методов решения, создавалось множество различных алгоритмов, применялись в практике новые методы, появлялась обширная литература.
Помимо методов решения задач линейного программирования, выпускались работы, содержащие методы динамического и нелинейного программирования.
Характеристика метода линейного программирования
Линейное программирование в экономическом анализе позволяет обосновать наиболее оптимальные экономические решения при жестких ограничениях, которые относятся к применяемым ресурсам в производстве (основные фонды, трудовые ресурсы, материалы и т.д.).
Применяя данный метод, можно решать задачи планирования деятельности предприятия. С его помощью можно определить оптимальную величину выпуска продукции, направления эффективного применения имеющихся производственных ресурсов.
Метод линейного программирования позволяет решать экстремальные задачи, когда определяются крайние значения, т.е. максимум и минимум функций переменных.
Линейное программирование применяется также при анализе переменных величин, когда имеют место определенные ограничивающие факторы.
Распространено решение транспортной задачи посредством линейного программирования. Сущность данной задачи состоит в минимизации затрат, которые возникают при эксплуатации транспортных средств в условиях ограничений относительно количества данных транспортных средств, продолжительности работы, грузоподъемности и т.д.
Помимо этого, линейное программирование позволяет решить задачу составления расписания. Необходимо распределить время функционирования персонала таким образом, чтобы оно было приемлемым для каждого сотрудника, а также для клиентов компании. Задача в данном случае состоит в максимизации количества клиентов при ограничениях количества персонала и рабочего времени.
Из всего вышесказанного следует, что линейное программирование в экономическом анализе весьма распространено: оно применяется при анализе использования и размещения ресурсов, при планировании и прогнозировании деятельности компании.
Общая задача линейного программирования
Среди большого количества оптимизационных задач выделяются задачи линейного программирования, которые имеют специфические черты.
В каждой задаче элементы решения – это ряд неотрицательных переменных $x_1, x_2,…, x_n$. Следует так выбирать значения данных переменных, чтобы:
- Действовали некоторые ограничения вида линейных неравенств или же неравенств в отношении переменных $x_1, x_2,…, x_n$.
- Линейная функция $f$ переменных являлась максимумом (минимумом).
Общая задача линейного программирования – это задача, где оптимизируемая функция цели является линейной комбинацией известных коэффициентов $c_j$ и неизвестных переменных $x_j$ вида:
Рисунок 1. Функция. Автор24 — интернет-биржа студенческих работ
Функция $f$ также называется целевой функцией или же критерием эффективности.
Найти решение задачи линейного программирования означает отыскать значения переменных $x_j$, которые удовлетворяют ограничениям, а целевая функция при таких значениях принимает максимальное или минимальное значение.
Экономический анализ решения задач линейного программирования
Сведем ограничения типа ≥ к ограничениям ≤ умножением на -1.
Так на все переменные наложены условия неотрицательности, то в двойственной задаче все ограничения будут являться неравентвами.
Так как ограничений в прямой задаче – два, то двойственная задача будет иметь две переменные, а так как прямая задача содержит три переменные, то двойственная задача будет иметь три ограничения.
Коэффициенты ограничений двойственной задачи получим транспонированием системы ограничений прямой задачи.
Двойственная задача является задачей на минимум, а ограничения имеют знаки ≥.
Учитывая указанные выше правила, имеем двойственную задачу:
Так как на переменные наложены условия неотрицательности, то ограничения двойственной задачи будут ограничениями-неравенствами. Так как ограничения прямой задачи являются равенствами, то на переменные двойственной задачи не накладывается условие неотрицательности.
Так как ограничений в прямой задаче – два, то двойственная задача будет иметь две переменные, а так как прямая задача содержит четыре переменные, то двойственная задача будет иметь четыре ограничения.
Коэффициенты ограничений двойственной задачи получим транспонированием системы ограничений прямой задачи.
Двойственная задача является задачей на минимум, а ограничения имеют знаки ≥.
В результате получим следующую модель двойственной задачи:
Анализ решения линейной задачи разберем на примере задачи определения оптимального ассортимента выпускаемой продукции.
Пусть задача имеет следующую математическую модель
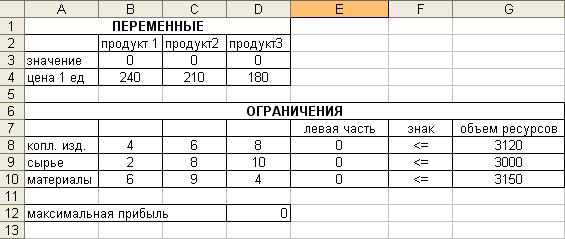
Пусть данные на листе Excel размещены следующим образом
х1=397,5; х2=0; х3=191,25 Fmax=129 825.
По результатам решения формируется три отчета: по результатам, по устойчивости, по пределам.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
4.3 Анализ решения задач линейного программирования
В математическом программировании доказывается следующая теорема двойственности (теорема об оценках).
Теорема 1. В оптимальном решении двойственной задачи значения переменных yi * (оценок) численно равны частным производным fmax / bi для исходной задачи.
Отсюда при малых изменениях bi свободных членов bi следует приближенное равенство
Некоторые аспекты применения двойственных оценок оптимального плана для его экономико-математического анализа рассмотрим на примере задачи рационального использования ресурсов по критерию максимума прибыли.
В матрично-векторной форме задача записывается следующим образом:
где — вектор прибыли продукции; — искомый вектор – план производства продукции; А- матрица коэффициентов при неизвестных – нормы потребления ресурсов; — вектор ограничений по ресурсам; — вектор оценок ресурсов.
Анализ задач линейного программирования может проводиться путем сопоставления различных вариантов решений; с помощью анализа внутренней структуры каждого из полученных решений, базирующегося на свойствах двойственных оценок, приведенных ниже.
Двойственные оценки являются:
- показателем дефицитности ресурсов и продукции. Это их свойство следует из теоремы. Величина yi* является оценкой i-го ресурса. Чем больше значение оценки yi*, тем выше дефицитность ресурса. Для недефицитного ресурса yi* = 0;
- показателем влияния ограничений на значение целевой функции. Ранее было отмечено, что yi* = fmax/bi. При незначительном приращении bi является точной мерой влияния ограничений на целевую функцию. Поэтому представляет интерес определение предельных значений ограничений (нижней и верхней границ), в которых величины оценок остаются неизменными;
- показателем эффективности производства отдельных видов продукции с позиции критерия оптимальности. Это свойство следует из теоремы. Его суть заключается в том, что в оптимальный план может быть включена лишь та продукция j-го вида, для которой выполняется условие
- инструментом сопоставления суммарных условных затрат и результатов. Это свойство следует из принципа двойственности, в котором устанавливается связь между значениями функций прямой и двойственной задач.
Из ранее данной экономической интерпретации двойственных задач следует, что равенство значений целевых функций при оптимальных планах означает, что оценка всех затрат производства должна равняться оценке производственного продукта.
Для целей анализа большое значение имеет матрица А -1 = dij, обратная матрице базиса оптимального плана A = аij.
Двойственные оценки можно использовать для экономического анализа решения при условии, что ограничения на ресурсы изменяются лишь в определенных пределах. В этой связи говорят о допустимом интервале устойчивости оценок. Интервал устойчивости оценок по отношению к i-му ограничению имеет вид
где называют нижним пределом уменьшения, а — верхним пределом увеличения и вычисляют по формулам:
Целесообразность включения в план новых видов продукции оценивается характеристикой
Пусть имеется возможность приобрести дополнительно i-й ресурс в объеме . Эта величина находится в пределах устойчивости двойственных оценок. Цена единицы ресурса равна ci. Следовательно, приращение прибыли в то время как затраты на приобретение ресурса составляют Данное мероприятие будет эффективным, если обеспечит дополнительную прибыль, т. е. если > 0, где
Пример. Для изготовления четырех видов продукции (А, Б, В и Г) используются три вида ресурсов (I, II, III). Наличие ресурсов, нормы их расхода на единицу продукции и получаемая прибыль от единицы продукции заданы в табл. Необходимо: а) найти оптимальные решения прямой и двойственной задач; б) определить изменение максимальной прибыли при изменении ресурсов: I вида – на -10ед., II – на +60, III – на +30 ед.; оценить раздельное и суммарное влияние этих изменений на величину максимальной прибыли; в) оценить целесообразность введения в план пятого вида продукции Д, нормы затрат ресурсов на единицу которого равны соответственно 2, 4, 2, а прибыль – 15; г) оценить целесообразность закупки 100 ед. ресурса III вида по цене c3 = 0,5.
Норма расхода на единицу продукции