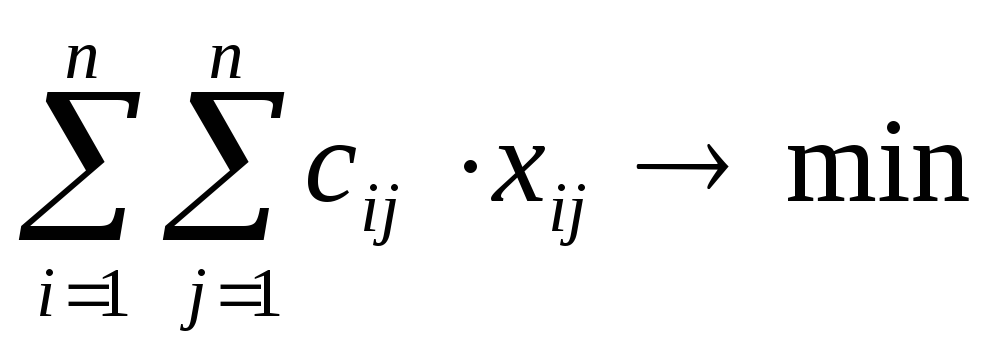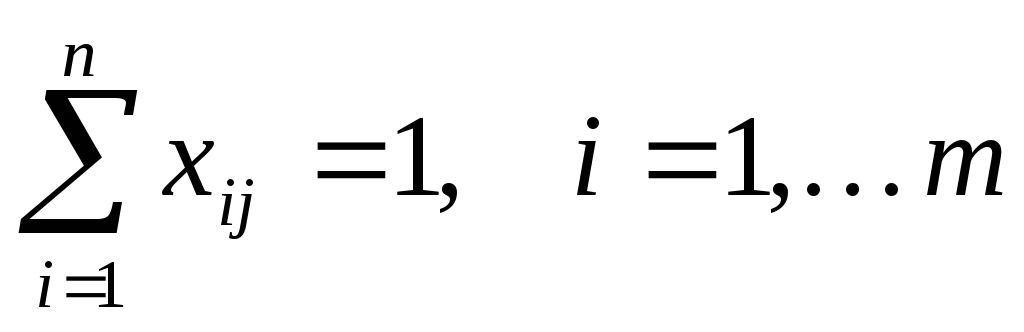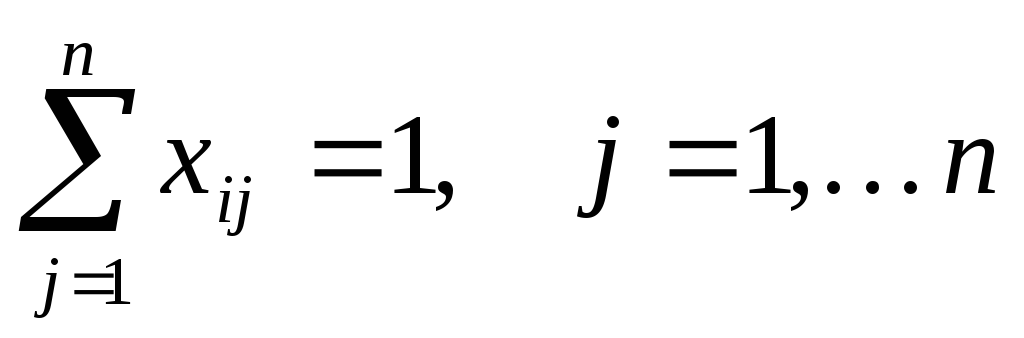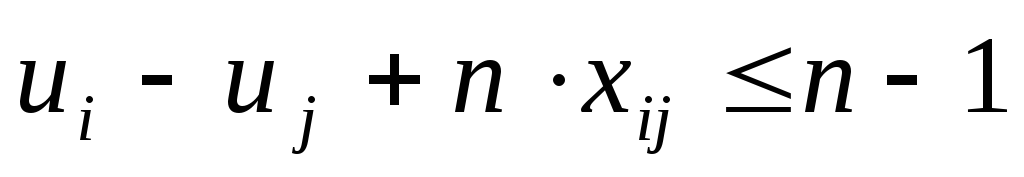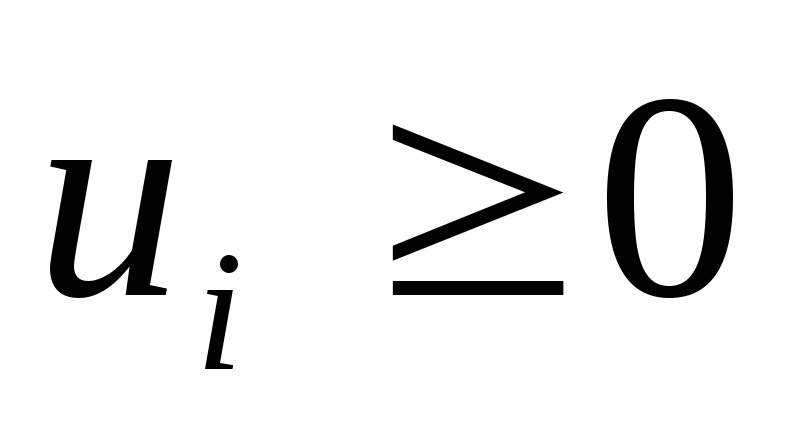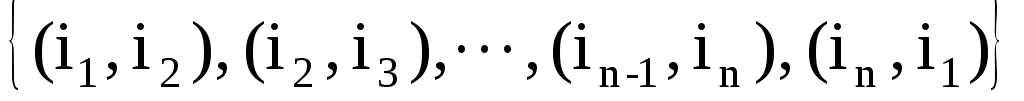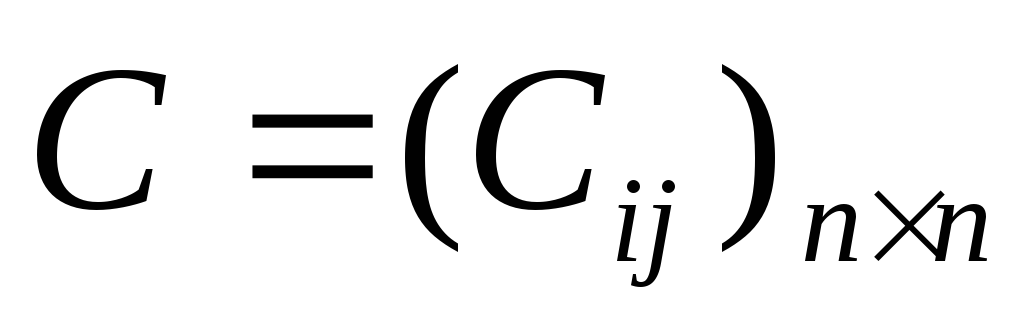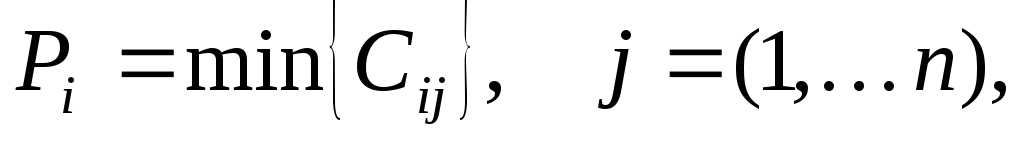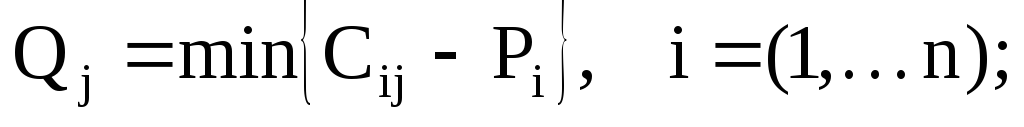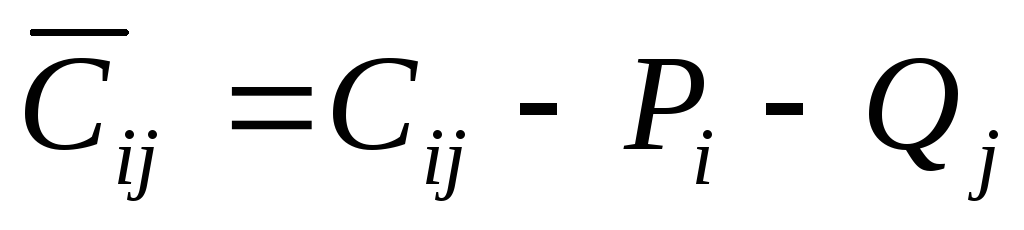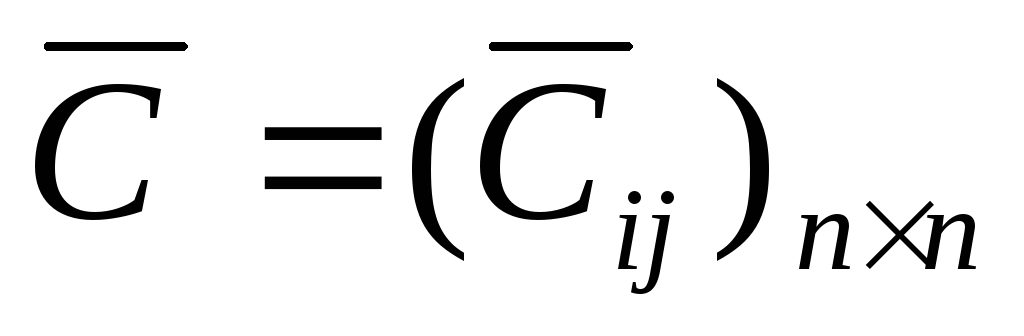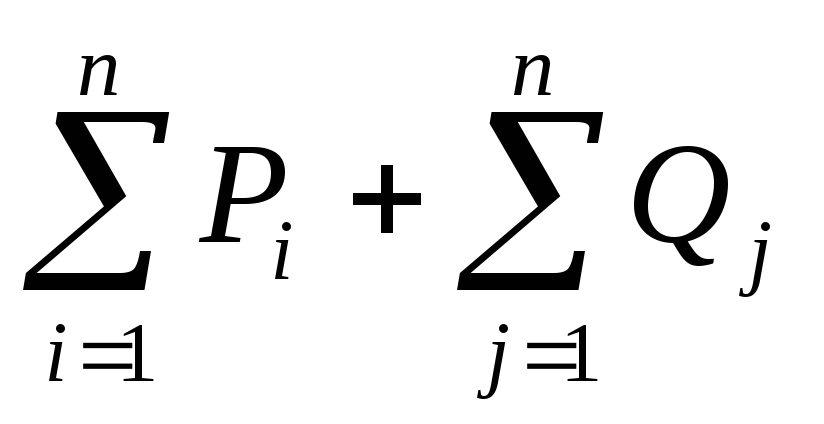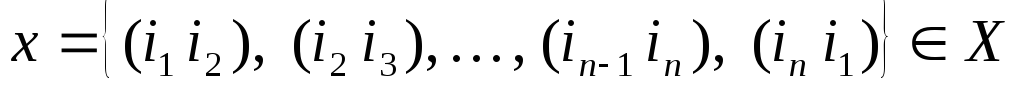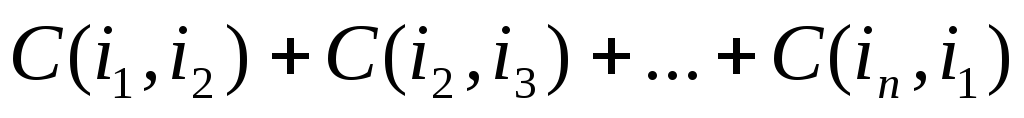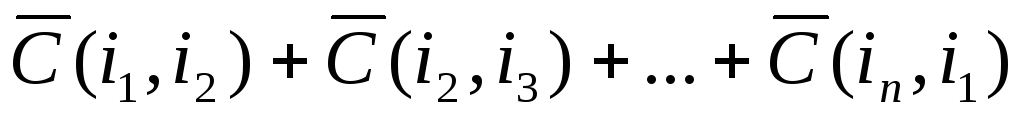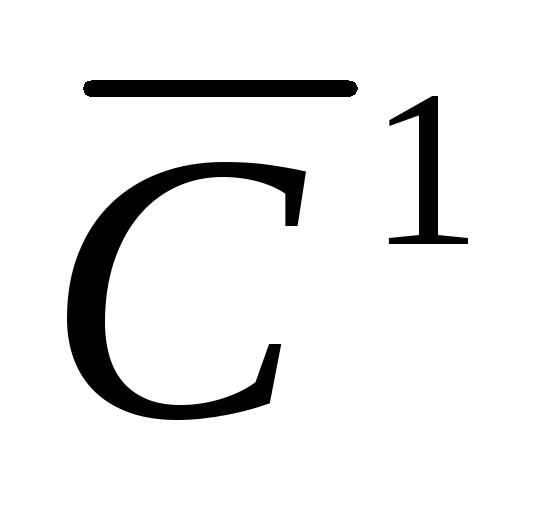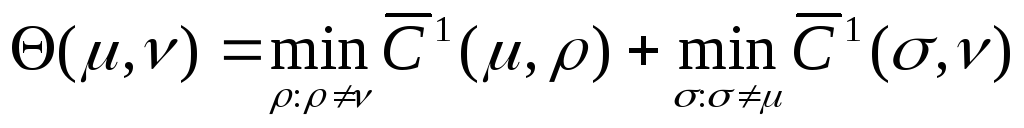Решение задачи коммивояжера
В задаче коммивояжера для формирования оптимального маршрута объезда n городов необходимо выбрать один лучший из (n-1)! вариантов по критерию времени, стоимости или длине маршрута. Эта задача связана с определением гамильтонова цикла минимальной длины. В таких случаях множество всех возможных решений следует представить в виде дерева — связного графа, не содержащего циклов и петель. Корень дерева объединяет все множество вариантов, а вершины дерева — это подмножества частично упорядоченных вариантов решений.
Инструкция . Выберите размерность матрицы (количество городов). Полученное онлайн решение сохраняется в файле Word и Excel (см. пример решения задачи коммивояжера).
Математическая модель задачи коммивояжера
Сформулированная задача — задача целочисленная. Пусть хij=1 , если путешественник переезжает из i -ого города в j -ый и хij=0 , если это не так.
Формально введем (n+1) город, расположенный там же, где и первый город, т.е. расстояния от (n+1) города до любого другого, отличного от первого, равны расстояниям от первого города. При этом, если из первого города можно лишь выйти, то в (n+1) город можно лишь придти.
Введем дополнительные целые переменные, равные номеру посещения этого города на пути. u1=0 , un+1=n . Для того, чтобы избежать замкнутых путей, выйти из первого города и вернуться в (n+1) введем дополнительные ограничения, связывающие переменные xij и переменные ui ( ui целые неотрицательные числа).
Методы решения задачи коммивояжера
- метод ветвей и границ (алгоритм Литтла или исключения подциклов). Пример решения методом ветвей и границ;
- венгерский метод. Пример решения венгерским методом.
5.2. Задача коммивояжера
Имеется n городов, пронумерованных числами 1, 2. n. Для любой пары городов (i, j) задано расстояние (время, путевые расходы) C(i,j) 0 между ними. Поэтому в общем случае C(i, j) C(j, i). Коммивояжер, выезжая из какого-либо города, должен посетить все города по одному разу и вернуться в исходный город. Необходимо определить такую последовательность объезда городов, при которой длина маршрута была бы минимальной.
Другая интерпретация этой задачи связана с минимизацией времени переналадок при обработке на одном станке партии из n различных деталей. Здесь C(i, j) – время переналадки при переходе от обработки детали i к обработке детали j. Требуется найти последовательность обработки деталей, минимизирующую общее время переналадок.
Для записи постановки задачи в терминах целочисленного линейного программирования определим переменные следующим образом: 
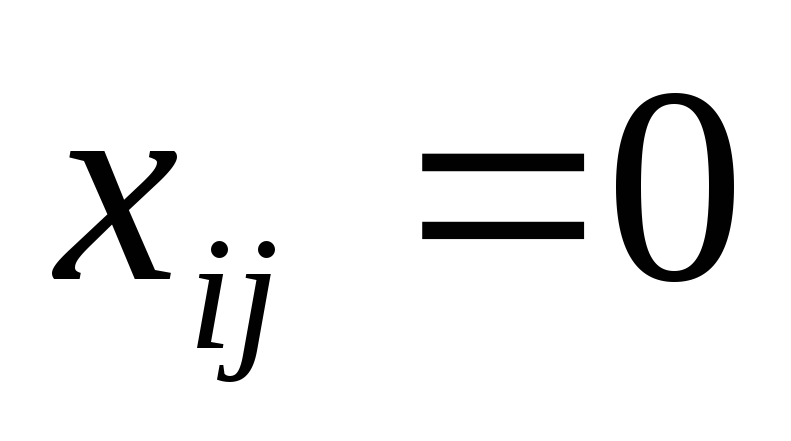
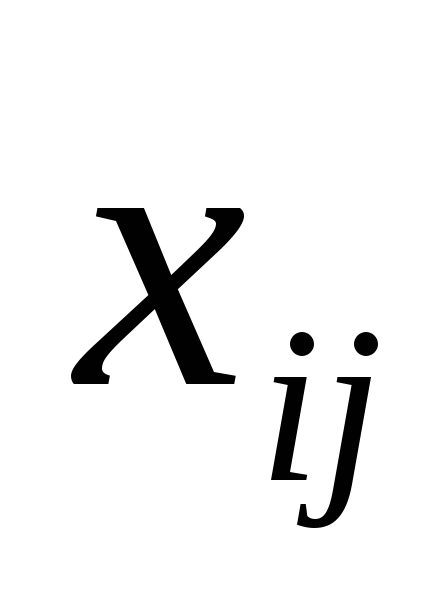
(5.1)
(въезд в город j); (5.2)
(выезд из города i); (5.3)
(i j); (5.4)
xij = , ,целые, i = 1, . m, j = 1, . n. (5.5)
Ограничения (5.4) требуют, чтобы маршрут образовывал контур.
Применение метода ветвей и границ для решения задачи коммивояжера
Допустимый маршрут х представим как множество упорядоченных пар городов:
х = .
Каждый допустимый маршрут представляет собой цикл, проходя по которому коммивояжер посещает каждый город ровно один раз и возвращается в исходный город. Каждая упорядоченная пара (i, j) является дугой маршрута. Длина F(х) маршрута х равна сумме соответствующих элементов C(i, j). Заметим, что множество всех допустимых маршрутов X содержит (n-1)! элементов.
Обозначим через матрицу расстояний. Чтобы запретить переезды вида (i,i), положим C(i, i) = +∞ (i = 1,…, n).
Пусть
.
Тогда – редуцированная матрица.
Пусть d(X) = – сумма констант редуцирования.
Тогда для любого маршрута
F(х) = =
= +d(X) ≥ d(X) (5.6)
Неравенство (5.6) показывает, что d(X) является оценкой снизу для множества Х. Кроме того, после редукции длины всех маршрутов уменьшаются на одну и ту же величину d(X) и, следовательно, оптимальный маршрут, найденный с использованием редуцированной матрицы, оптимален и для исходной задачи.
Ветвление
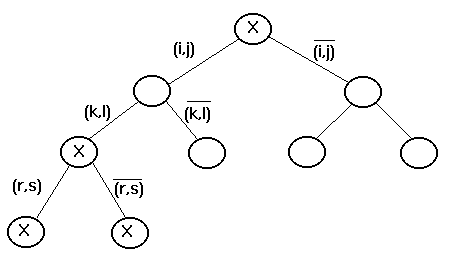
Процесс ветвления можно представить в виде дерева, каждая вершина которого соответствует некоторому множеству маршрутов, являющемуся подмножеством множества Х. При этом начальная вершина соответствует множеству всех маршрутов Х (рис. 5.6).
Рис. 5.6. Ветвление
На каждом шаге из числа кандидатов на ветвление выбирается множество Х 1 с наименьшей оценкой. Оно разветвляется на два подмножества 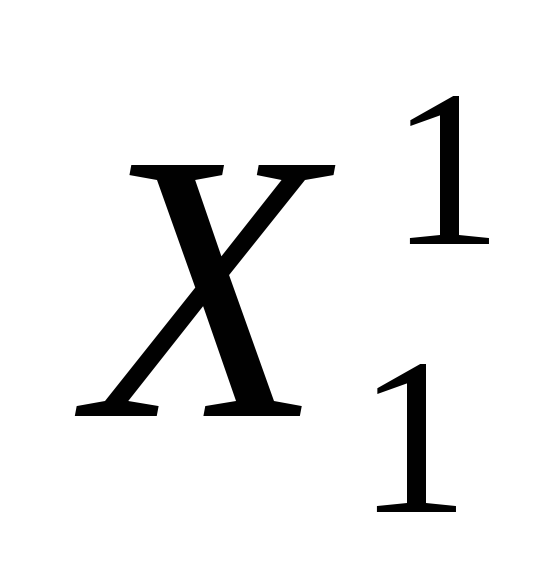
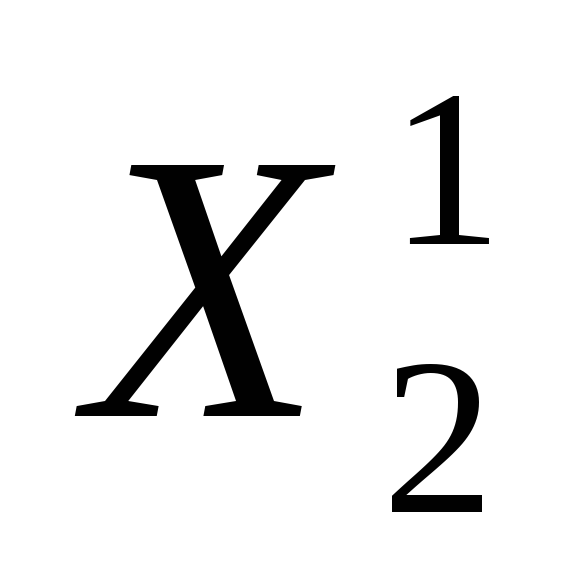
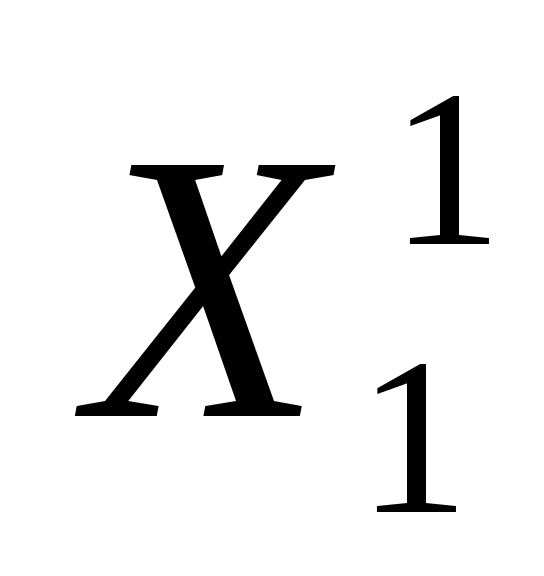
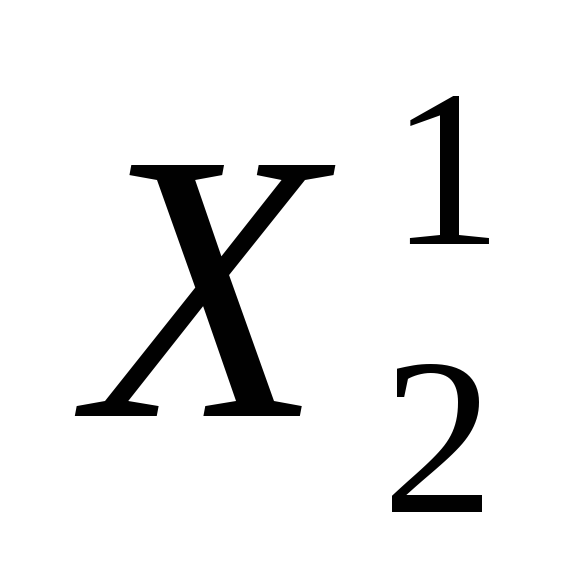
Ребро дерева, соединяющее вершины Х 1 и 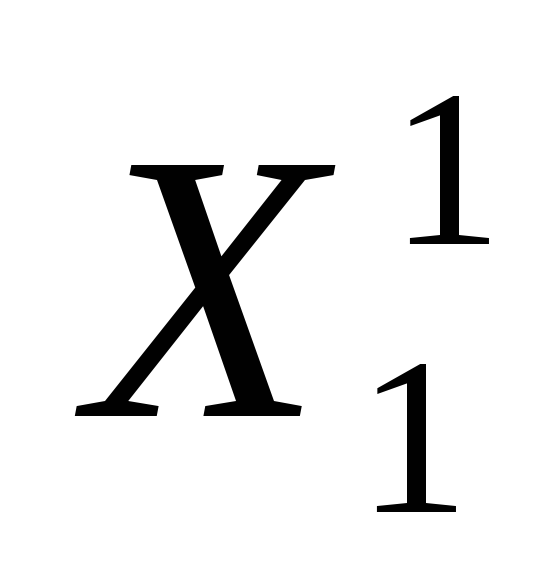
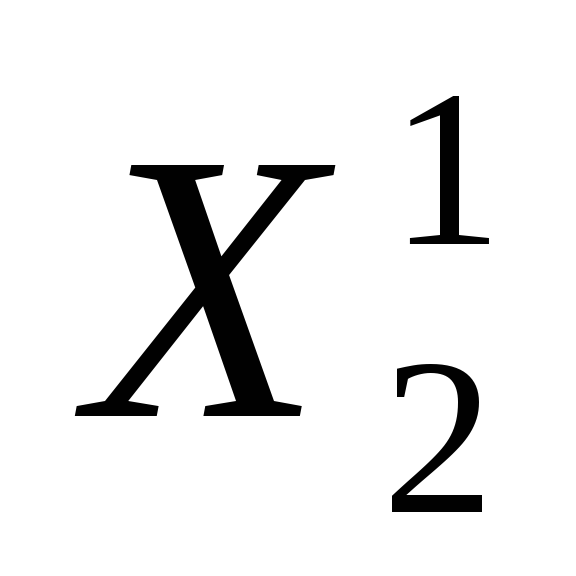
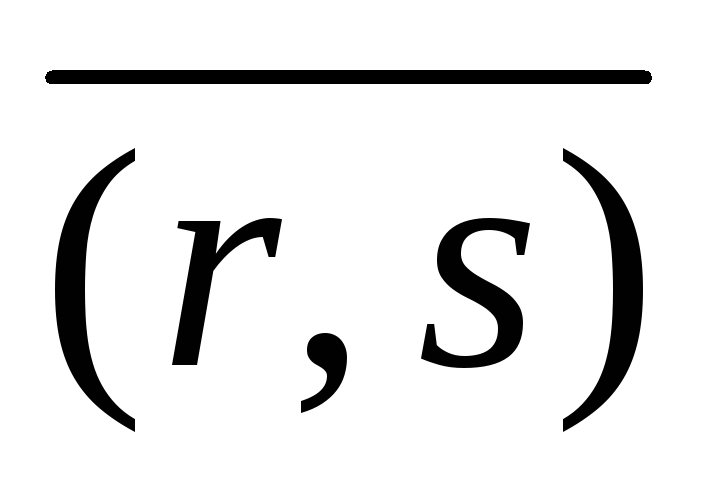
Пусть 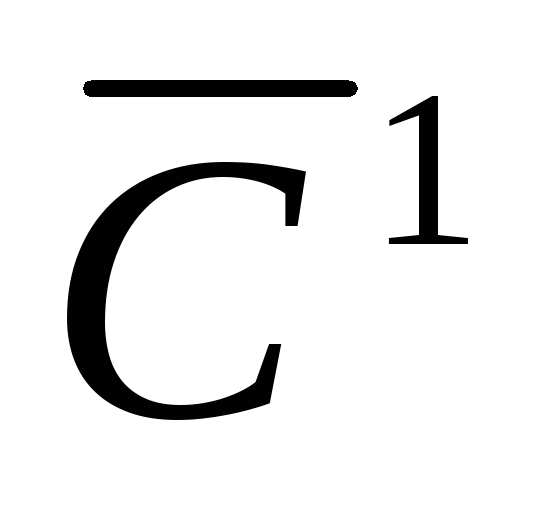
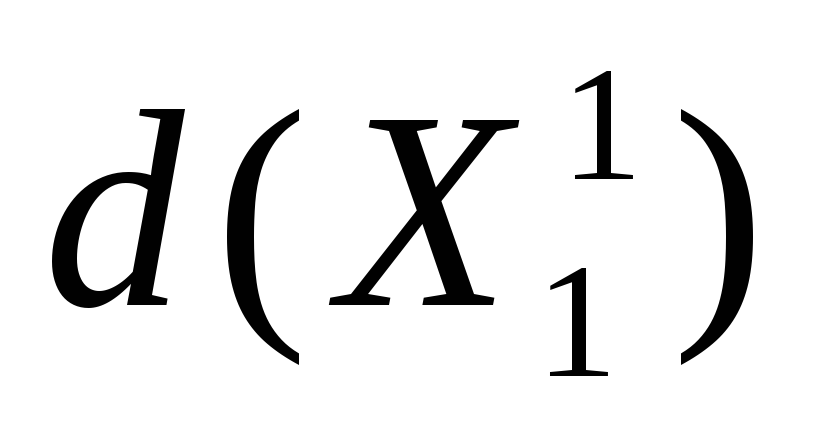
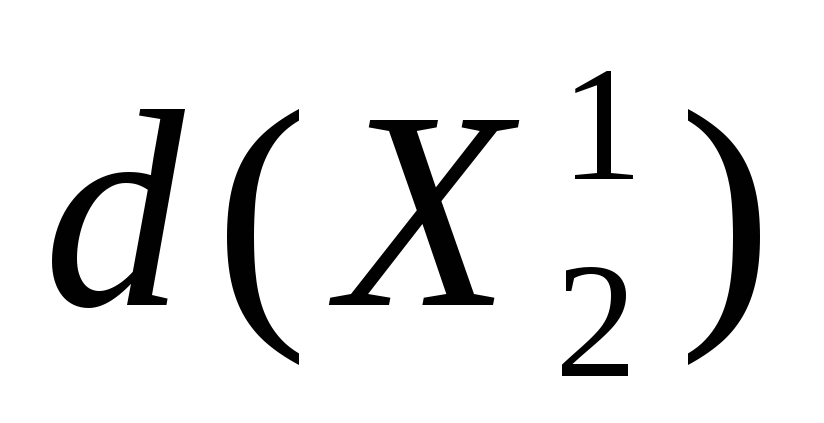
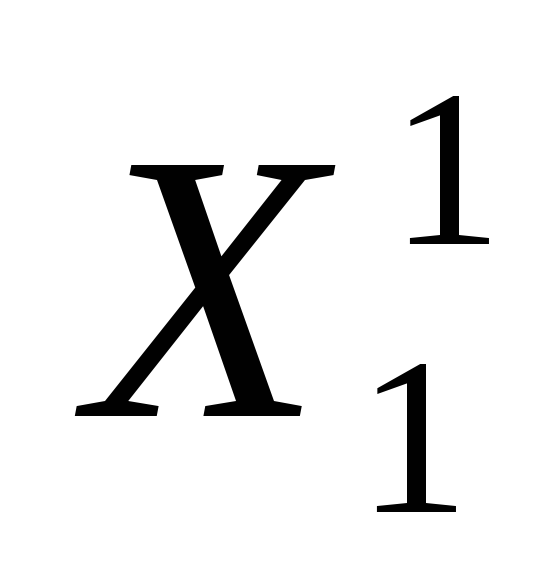
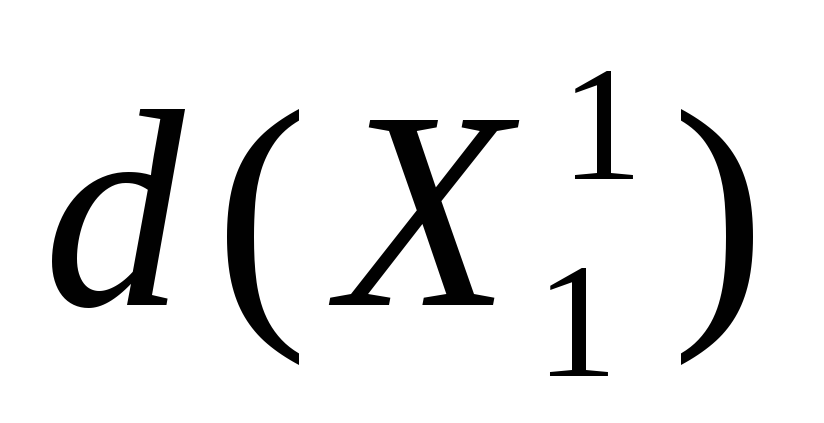
(,) = 0, (5.7)
поскольку все маршруты множества 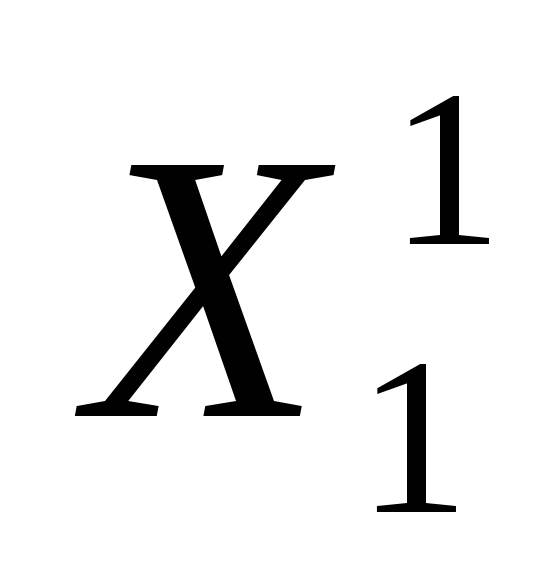
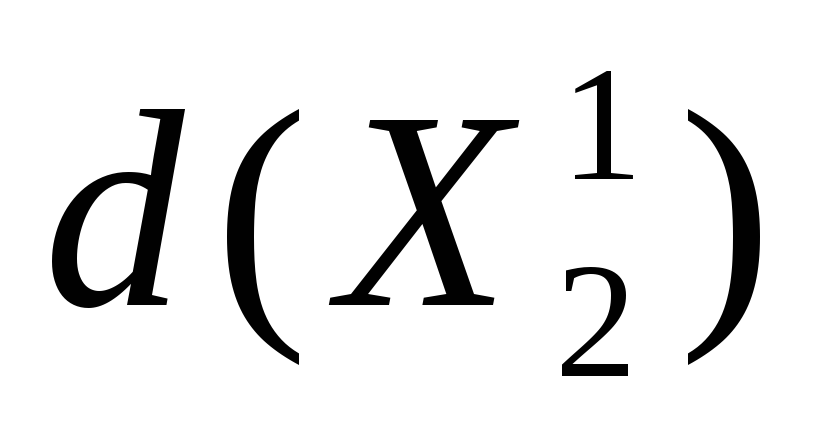
Смысл введения функции