Задача 8 ферзей java

Решение задачи о 8 Ферзях с помощью массива

Каждый, наверное, сталкивался с задачей расстановки 8 ферзей на шахматной доске.
Рассмотрим решение данной задачи с использованием массива.

Итак, имеем одномерный массив состоящий из 8 элементов. Индексные значения — это строки, а значения в архиве по соответствующим индексам — это столбец шахматной доски соответственно.

Для того, чтобы мы оставили Ферзя в покое и начали перемещать следующего, должны отсутствовать иные Ферзи:
1. по вертикали
2. по диагоналям
3. по горизонтали

Третий пункт в данном методе решения этой задачи можно исключить сразу, так как два Ферзя в одной строке мы изначально не рассматриваем.

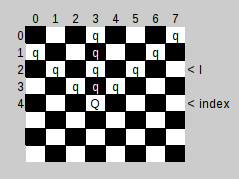
На рисунке показано, какие поля попадают под «бой» (Q — устанавливаемый Ферзь, q — поля на которых не должно быть других.)

Из чего получаем, что нам необходимо для исключения вертикали сравнить равенство номер столбцов, а для исключения диагоналей сравнить модуль разницы столбцов с разницей строк у устанавливаемого и проверяемого Ферзей.

Вот что мы в итоге получаем:

public class Ferzi2 < static int[] chessboard = ; static int index = 0; static int version = 0; public static void main(String[] args)

Данная статья не подлежит комментированию, поскольку её автор ещё не является полноправным участником сообщества. Вы сможете связаться с автором только после того, как он получит приглашение от кого-либо из участников сообщества. До этого момента его username будет скрыт псевдонимом.

О песочнице

Это «Песочница» — раздел, в который попадают дебютные публикации пользователей, желающих стать полноправными участниками сообщества.

Если у вас есть приглашение, отправьте его автору понравившейся публикации — тогда её смогут прочитать и обсудить все остальные пользователи Хабра.

Чтобы исключить предвзятость при оценке, все публикации анонимны, псевдонимы показываются случайным образом.

О модерации

• рекламные и PR-публикации
• вопросы и просьбы (для них есть Хабр Q&A);
• вакансии (используйте Хабр Карьеру)
• статьи, ранее опубликованные на других сайтах;
• статьи без правильно расставленных знаков препинания, со смайликами, с обилием восклицательных знаков, неоправданным выделением слов и предложений и другим неуместным форматированием текста;
• жалобы на компании и предоставляемые услуги;
• низкокачественные переводы;
• куски программного кода без пояснений;
• односложные статьи;
• статьи, слабо относящиеся к или не относящиеся к ней вовсе.

Источник

Русские Блоги

Используйте рекурсивное мышление и алгоритм поиска с возвратом для решения проблемы восьми ферзей (реализация на Java)

Задача восьми королев

Проблема восьми ферзей — старая и хорошо известная проблема и типичный случай алгоритмов поиска с возвратом. Проблема была поднята шахматистом Максом Бетелем в 1848 году: поместите восемь ферзей на шахматную доску 8 × 8 так, чтобы они не могли атаковать друг друга, то есть две ферзя не могут находиться в одном ряду. Спросите, сколько путей находится в одном столбце или на одной диагональной линии. Гаусс считает, что существует 76 вариантов. В 1854 году разные авторы опубликовали 40 различных решений в Chess Magazine в Берлине. Позже кто-то решил 92 вида результатов, используя теорию графов. После изобретения компьютера существует множество компьютерных языков, которые могут решить эту проблему.

Введение в проблему

Проблема восьми ферзей — это проблема, основанная на шахматах: как можно разместить восемь ферзей на шахматной доске 8 × 8, чтобы ни один ферзь не мог напрямую взять других ферзей? Для достижения этой цели никакие две ферзя не могут находиться на одной горизонтальной, вертикальной или диагональной линии. Проблема восьми ферзей может быть обобщена на более общую проблему размещения n ферзей: размер доски становится n1 × n1, а количество ферзей также становится n2. И проблема может быть решена только при n2 ≥ 1 или n1 ≥ 4.
Задача о восьми ферзях была впервые предложена шахматистом Максом Бетелем в 1848 году. После этого математики продолжили его изучение, включая Гаусса и Кантора, и обобщили его на более общую проблему размещения n ферзей. Первое решение проблемы восьми ферзей было дано Францем Ноком в 1850 году. Knock был также одним из первых, кто обобщил проблему на более общую проблему размещения n ферзей. В 1874 году С. Гундель предложил метод решения по определителю, который позже был усовершенствован Дж. В. Л. Глешером.
Азгер Дейкстра использовал этот вопрос в 1972 году в качестве примера, чтобы проиллюстрировать свои способности так называемого структурного программирования.
Проблема восьми королев появилась у седьмого посетителя знаменитой видеоигры в начале 1990-х годов.

проблема решена.

Первый:

Самый глупый способ — определить 8 циклов for. . . .

Второй тип: алгоритм поиска с возвратом.

Код

public class Queen  private int[] column; // Есть ли ферзь в том же столбце, 1 означает, что есть private int[] rup; // Есть ли ферзь сверху справа налево снизу private int[] lup; // Есть ферзь сверху слева направо снизу private int[] queen; //ответ private int num; // Номер решения public Queen()  column = new int[8+1]; rup = new int[(2*8)+1]; lup = new int[(2*8)+1]; for (int i = 1; i  8; i++) column[i] = 0; for (int i = 1; i  (2*8); i++) rup[i] = lup[i] = 0; // Исходное определение - все без ферзя queen = new int[8+1]; > public void backtrack(int i)  if (i > 8)  showAnswer(); > else  for (int j = 1; j  8; j++)  if ((column[j] == 0) && (rup[i+j] == 0) && (lup[i-j+8] == 0))  // Если ферзя нет queen[i] = j; // Установить как занятый column[j] = rup[i+j] = lup[i-j+8] = 1; backtrack(i+1); // Вызов цикла column[j] = rup[i+j] = lup[i-j+8] = 0; > > > > protected void showAnswer()  num++; System.out.println("\ nОтвет" + num); for (int y = 1; y  8; y++)  for (int x = 1; x  8; x++)  if(queen[y]==x)  System.out.print("Q"); > else  System.out.print("."); > > System.out.println(); > > public static void main(String[] args)  Queen queen = new Queen(); queen.backtrack(1); > > 

Третий тип: рекурсивный вызов

Код

package p03.Рекурсия; /* * Линия 1 * 1 * Строка 2 * 3 * Строка 3 * 5 * Строка 4 * 2 X * Строка 5 * 4 X * Строка 6 * X * 8 X * Строка 6 * X * 7 * Строка 5 * 2 X * Строка 6 X * 4 X * Строка 7 * 6 X * Строка 8 * X * 4 * . * * 8 * 6 * 7 * 8 * 4 * 5 * 6 * 7 * 8 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * */ public class EightQueen  private static int count=0; // Записываем первую возможность private static int N=8; public static void main(String[] args)  int[][] arr=new int[N][N]; // Элемент по умолчанию - 0 1, когда ферзь eightQueen(0,arr); // Вывести все возможные решения восьми ферзей и начать с первой строки 0 > //row [0,7] private static void eightQueen(int row, int[][] arr)  if(row==N)// Условие печати, при условии, что это 8 ферзей, оно будет печататься каждый раз, когда достигнет 9-й строки. count++; System.out.println(" "+count+"Виды:"); for(int i=0;iarr.length;i++) for(int j=0;jarr[i].length;j++) System.out.print(arr[i][j]+" "); > System.out.println(); > >else // Делаем резервную копию массива int[][] newArr=new int[N][N]; for(int i=0;iarr.length;i++) for(int j=0;jarr[i].length;j++) newArr[i][j]=arr[i][j]; > > for(int col=0;colN;col++) /* Определите, есть ли ферзь вверху, вверху слева и вверху справа от текущего элемента. */ if(noDangerous(row,col,newArr)) for(int c=0;cN;c++) newArr[row][c]=0;// Устанавливаем ферзя в других позициях текущей строки на 0 > newArr[row][col]=1; eightQueen(row+1, newArr); > > > > private static boolean noDangerous(int row, int col, int[][] newArr)  //Наверху for(int r=row-1;r>=0;r--) if(newArr[r][col]==1) return false; > > //Верхний левый for(int r=row-1,c=col-1;r>=0&&c>=0;r--,c--) if(newArr[r][c]==1) return false; > > //В правом верхнем углу for(int r=row-1,c=col+1;r>=0&&cN;r--,c++) if(newArr[r][c]==1) return false; > > return true; > > 

Источник

Решение задачи о 8 Ферзях с помощью массива

2015-03-01 в 10:06, admin , рубрики: Песочница, метки: java, ненормальное программирование, Программирование

Каждый, наверное, сталкивался с задачей расстановки 8 ферзей на шахматной доске.
Рассмотрим решение данной задачи с использованием массива.

Итак, имеем одномерный массив состоящий из 8 элементов. Индексные значения — это строки, а значения в архиве по соответствующим индексам — это столбец шахматной доски соответственно.

Для того, чтобы мы оставили Ферзя в покое и начали перемещать следующего, должны отсутствовать иные Ферзи:
1. по вертикали
2. по диагоналям
3. по горизонтали

Третий пункт в данном методе решения этой задачи можно исключить сразу, так как два Ферзя в одной строке мы изначально не рассматриваем.

На рисунке показано, какие поля попадают под «бой» (Q — устанавливаемый Ферзь, q — поля на которых не должно быть других.)

Из чего получаем, что нам необходимо для исключения вертикали сравнить равенство номер столбцов, а для исключения диагоналей сравнить модуль разницы столбцов с разницей строк у устанавливаемого и проверяемого Ферзей.

Вот что мы в итоге получаем:

public class Ferzi2 < static int[] chessboard = ; static int index = 0; static int version = 0; public static void main(String[] args) < do < if (checking())< if (index == 7) < System.out.println(version++ + " [0]=" + chessboard[0] + " [1]=" + chessboard[1] + " [2]=" + chessboard[2] + " [3]=" + chessboard[3] + " [4]=" + chessboard[4] + " [5]=" + chessboard[5] + " [6]=" + chessboard[6] + " [7]=" + chessboard[7]); chessboard[index]++; >else < index++; >> else < chessboard[index]++; >> while (chessboard[0] <8); >static boolean checking() < int i; if (index == 0) < return true; >if (chessboard[index]>7) < chessboard[index] = 0; index--; return false; >for (i=0;i > return true; > > 

Источник