Задача 3 диагональная матрица python

Получить все диагонали в матрице / списке списков в Python

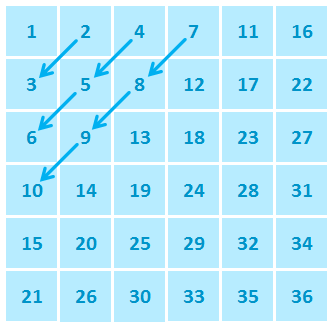
Я ищу питоновский способ получить все диагонали (квадратной) матрицы, представленные в виде списка списков. Предположим, что у меня есть следующая матрица:

matrix = [[-2, 5, 3, 2], [ 9, -6, 5, 1], [ 3, 2, 7, 3], [-1, 8, -4, 8]] 

l = len(matrix[0]) print [matrix[i][i] for i in range(l)] # [-2, -6, 7, 8] print [matrix[l-1-i][i] for i in range(l-1,-1,-1)] # [ 2, 5, 2, -1] 

[[-2], [9, 5], [3,-6, 3], [-1, 2, 5, 2], [8, 7, 1], [-4, 3], [8], [2], [3,1], [5, 5, 3], [-2, -6, 7, 8], [9, 2, -4], [3, 8], [-1]] 

7 ответов

import numpy as np matrix = np.array( [[-2, 5, 3, 2], [ 9, -6, 5, 1], [ 3, 2, 7, 3], [-1, 8, -4, 8]]) diags = [matrix[::-1,:].diagonal(i) for i in range(-3,4)] diags.extend(matrix.diagonal(i) for i in range(3,-4,-1)) print [n.tolist() for n in diags] 

Выход

[[-2], [9, 5], [3, -6, 3], [-1, 2, 5, 2], [8, 7, 1], [-4, 3], [8], [2], [3, 1], [5, 5, 3], [-2, -6, 7, 8], [9, 2, -4], [3, 8], [-1]] 

import numpy as np # Alter dimensions as needed x,y = 3,4 # create a default array of specified dimensions a = np.arange(x*y).reshape(x,y) print a print # a.diagonal returns the top-left-to-lower-right diagonal "i" # according to this diagram: # # 0 1 2 3 4 . # -1 0 1 2 3 # -2 -1 0 1 2 # -3 -2 -1 0 1 # : # # You wanted lower-left-to-upper-right and upper-left-to-lower-right diagonals. # # The syntax a[slice,slice] returns a new array with elements from the sliced ranges, # where "slice" is Python [start[:stop[:step]] format. # "::-1" returns the rows in reverse. ":" returns the columns as is, # effectively vertically mirroring the original array so the wanted diagonals are # lower-right-to-uppper-left. # # Then a list comprehension is used to collect all the diagonals. The range # is -x+1 to y (exclusive of y), so for a matrix like the example above # (x,y) = (4,5) = -3 to 4. diags = [a[::-1,:].diagonal(i) for i in range(-a.shape[0]+1,a.shape[1])] # Now back to the original array to get the upper-left-to-lower-right diagonals, # starting from the right, so the range needed for shape (x,y) was y-1 to -x+1 descending. diags.extend(a.diagonal(i) for i in range(a.shape[1]-1,-a.shape[0],-1)) # Another list comp to convert back to Python lists from numpy arrays, # so it prints what you requested. print [n.tolist() for n in diags] 

Выход

[[ 0 1 2 3] [ 4 5 6 7] [ 8 9 10 11]] [[0], [4, 1], [8, 5, 2], [9, 6, 3], [10, 7], [11], [3], [2, 7], [1, 6, 11], [0, 5, 10], [4, 9], [8]] 

Источник

Линейная алгебра на Python. [Урок 1]. Создание Матрицы. Общие понятия

Эта статья открывает список уроков на тему “Линейная алгебра с примерами на Python“ . Мы постараемся рассказать о базовых понятиях линейной алгебры, которые могут быть полезны тем, кто занимается машинным обучением и анализом данных, и будем сопровождать все это примерами на языке Python .

Матрицы

Матрицей в математике называют объект, записываемый в виде прямоугольной таблицы, элементами которой являются числа (могут быть как действительные, так и комплексные). Пример матрицы приведен ниже.

В общем виде матрица записывается так:

Представленная выше матрица состоит из i-строк и j-столбцов. Каждый ее элемент имеет соответствующее позиционное обозначение, определяемое номером строки и столбца на пересечении которых он расположен: \(a_\)- находится на i-ой строке и j-м столбце.

Важным элементом матрицы является главная диагональ , ее составляют элементы, у которых совпадают номера строк и столбцов.

Виды матриц и способы их создания в Python

Матрица в Python – это двумерный массив, поэтому задание матриц того или иного вида предполагает создание соответствующего массива. Для работы с массивами в Python используется тип данных список (англ. list ). Но с точки зрения представления матриц и проведения вычислений с ними списки – не очень удобный инструмент, для этих целей хорошо подходит библиотека Numpy , ее мы и будем использовать в дальнейшей работе.

Напомним, для того, чтобы использовать библиотеку Numpy ее нужно предварительно установить, после этого можно импортировать в свой проект. По установке Numpy можно подробно прочитать в разделе “Установка библиотеки Numpy” из введения. Для того чтобы импортировать данный модуль, добавьте в самое начало программы следующую строку

Если после импорта не было сообщений об ошибке, то значит все прошло удачно и можно начинать работу. Numpy содержит большое количество функций для работы с матрицами, которые мы будем активно использовать. Обязательно убедитесь в том, что библиотека установлена и импортируется в проект без ошибок.

Рассмотрим, различные варианты матриц и способы их задания в Python .

Вектор

Вектором называется матрица, у которой есть только один столбец или одна строка. Более подробно свойства векторов, их геометрическая интерпретация и операции над ними будут рассмотрены в “ Главе 2 Векторная алгебра” .

Вектор-строка

Вектор-строка имеет следующую математическую запись.

Такой вектор в Python можно задать следующим образом.

>>> v_hor_np = np.array([1, 2]) >>> print(v_hor_np ) [1 2]

Если необходимо создать нулевой или единичный вектор , то есть вектор, у которого все элементы нули либо единицы, то можно использовать специальные функции из библиотеки Numpy .

Создадим нулевую вектор-строку размера 5 .

>>> v_hor_zeros_v1 = np.zeros((5,)) >>> print(v_hor_zeros_v1 ) [0. 0. 0. 0. 0.]

В случае, если требуется построить вектор-строку так, чтобы она сама являлась элементом какого-то массива, это нужно для возможности транспонирования матрицы (см. раздел “ 1.3 Транспонирование матрицы” ), то данную задачу можно решить так.

>>> v_hor_zeros_v2 = np.zeros((1, 5)) >>> print(v_hor_zeros_v2 ) [[0. 0. 0. 0. 0.]]

Построим единичную вектор-строку в обоих из представленных для нулевого вектора-строки форм.

>>> v_hor_one_v1 = np.ones((5,)) >>> print(v_hor_one_v1) [1. 1. 1. 1. 1.]

>>> v_hor_one_v2 = np.ones((1, 5)) >>> print(v_hor_one_v2) [[1. 1. 1. 1. 1.]]

Вектор-столбец

Вектор-столбец имеет следующую математическую запись.

В общем виде вектор столбец можно задать следующим образом.

>>> v_vert_np = np.array([[1], [2]]) >>> print(v_vert_np) [[1] [2]]

Рассмотрим способы создания нулевых и единичных векторов-столбцов. Построим нулевой вектор-столбец .

>>> v_vert_zeros = np.zeros((5, 1)) >>> print(v_vert_zeros) [[0.] [0.] [0.] [0.] [0.]]

Единичный вектор-столбец можно создать с помощью функции ones() .

>>> v_vert_ones = np.ones((5, 1)) >>> print(v_vert_ones) [[1.] [1.] [1.] [1.] [1.]]

Квадратная матрица

Довольно часто, на практике, приходится работать с квадратными матрицами . Квадратной называется матрица, у которой количество столбцов и строк совпадает. В общем виде они выглядят так.

Создадим следующую матрицу.

В Numpy можно создать квадратную матрицу с помощью метода array() .

>>> m_sqr_arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> print(m_sqr_arr) [[1 2 3] [4 5 6] [7 8 9]]

Как вы уже наверное заметили, аргументом функции np.array() является список Python , его можно создать отдельно и передать в функцию.

>>> m_sqr = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] >>> m_sqr_arr = np.array(m_sqr) >>> print(m_sqr_arr) [[1 2 3] [4 5 6] [7 8 9]]

Но в Numpy есть еще одни способ создания матриц – это построение объекта типа matrix с помощью одноименного метода. Задать матрицу можно в виде списка.

>>> m_sqr_mx = np.matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> print(m_sqr_mx) [[1 2 3] [4 5 6] [7 8 9]]

Также доступен стиль Matlab , когда между элементами ставятся пробелы, а строки разделяются точкой с запятой, при этом такое описание должно быть передано в виде строки.

>>> m_sqr_mx = np.matrix('1 2 3; 4 5 6; 7 8 9') >>> print(m_sqr_mx) [[1 2 3] [4 5 6] [7 8 9]]

Диагональная матрица

Особым видом квадратной матрицы является диагональная – это такая матрица, у которой все элементы, кроме тех, что расположены на главной диагонали, равны нулю.

Диагональную матрицу можно построить вручную, задав только значения элементам на главной диагонали.

>>> m_diag = [[1, 0, 0], [0, 5, 0], [0, 0, 9]] >>> m_diag_np = np.matrix(m_diag) >>> print(m_diag_np) [[1 0 0] [0 5 0] [0 0 9]]

Библиотека Numpy предоставляет инструменты, которые могут упростить построение такой матрицы.

Первый вариант подойдет в том случае, если у вас уже есть матрица, и вы хотите сделать из нее диагональную. Создадим матрицу размера 3 3 .

>>> m_sqr_mx = np.matrix('1 2 3; 4 5 6; 7 8 9')

Извлечем ее главную диагональ.

>>> diag = np.diag(m_sqr_mx) >>> print(diag) [1 5 9]

Построим диагональную матрицу на базе полученной диагонали.

>>> m_diag_np = np.diag(np.diag(m_sqr_mx)) >>> print(m_diag_np) [[1 0 0] [0 5 0] [0 0 9]]

Второй вариант подразумевает построение единичной матрицы, ей будет посвящен следующий параграф.

Единичная матрица

Единичной матрицей называют такую квадратную матрицу, у которой элементы главной диагонали равны единицы, а все остальные нулю.

Создадим единичную матрицу на базе списка, который передадим в качестве аргумента функции matrix() .

>>> m_e = [[1, 0, 0], [0, 1, 0], [0, 0, 1]] >>> m_e_np = np.matrix(m_e) >>> print(m_e_np) [[1 0 0] [0 1 0] [0 0 1]]

Такой способ не очень удобен, к счастью для нас, для построения такого типа матриц в библиотеке Numpy есть специальная функция – eye() .

>>> m_eye = np.eye(3) >>> print(m_eye) [[ 1. 0. 0.] [ 0. 1. 0.] [ 0. 0. 1.]]

В качестве аргумента функции передается размерность матрицы, в нашем примере – это матрица 3 3 . Тот же результат можно получить с помощью функции identity() .

>>> m_idnt = np.identity(3) >>> print(m_idnt) [[ 1. 0. 0.] [ 0. 1. 0.] [ 0. 0. 1.]]

Нулевая матрица

У нулевой матрицы все элементы равны нулю.

Пример того, как создать такую матрицу с использованием списков, мы приводить не будем, он делается по аналогии с предыдущим разделом. Что касается Numpy , то в составе этой библиотеки есть функция zeros() , которая создает нужную нам матрицу.

>>> m_zeros = np.zeros((3, 3)) >>> print(m_zeros) [[ 0. 0. 0.] [ 0. 0. 0.] [ 0. 0. 0.]]

В качестве параметра функции zeros() передается размерность требуемой матрицы в виде кортежа из двух элементов, первый из которых – число строк, второй – столбцов. Если функции zeros() передать в качестве аргумента число, то будет построен нулевой вектор-строка, это мы делали в параграфе, посвященном векторам.

Задание матрицы в общем виде

Если у вас уже есть данные о содержимом матрицы, то создать ее можно используя списки Python или функцию matrix() из библиотеки Numpy .

>>> m_mx = np.matrix('1 2 3; 4 5 6') >>> print(m_mx) [[1 2 3] [4 5 6]]

Если же вы хотите создать матрицу заданного размера с произвольным содержимым, чтобы потом ее заполнить, проще всего для того использовать функцию zeros() , которая создаст матрицу заданного размера, заполненную нулями.

>>> m_var = np.zeros((2, 5)) >>> print(m_var) [[ 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0.]]

P.S.

Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта . Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.

Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.

Источник

Задача 3 диагональная матрица python

В первой строке подаются высота и ширина холста – натуральные числа w и h (1 ≤ w, h ≤ 100); во второй – целое число n, количество прямоугольников (0 ≤ n ≤ 5000). Затем программа получает n строк с координатами левого верхнего и правого нижнего углов прямоугольников – x1, y1, x2, y2.

Целое число – площадь незакрашенной поверхности холста.

Примеры ввода и вывода

Строка с числами n и m, разделенными пробелом.

Матрица, заполненная в соответствии с условием задачи.

Пример ввода и вывода

В первой строке подается число n – количество строк. Затем программа получает n строк с элементами матрицы.

Максимальный элемент из заштрихованной области матрицы.

Пример ввода и вывода

Пример ввода и вывода

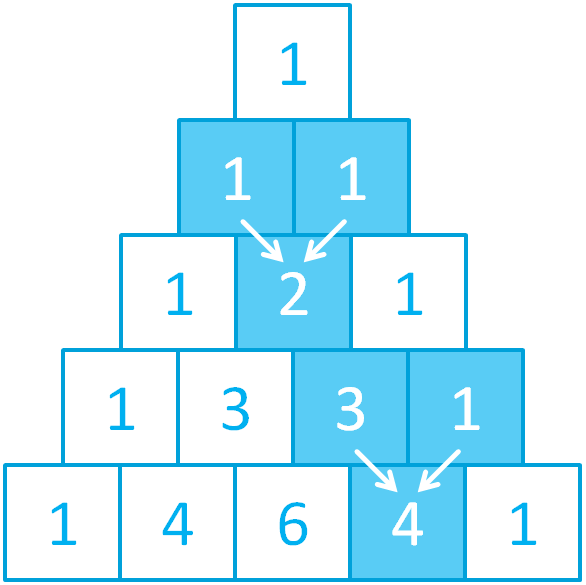
Решение

def trianglePascal(n): if n == 0: return [1] else: st = trianglePascal(n - 1) return [1] + [st[i] + st[i+1] for i in range(n - 1)] + [1] n = int(input()) print(trianglePascal(n)) 

n = int(input()) li = [1] for i in range(n): for j in range(len(li) - 1): li[j] = li[j] + li[j + 1] li.insert(0, 1) print(li) 

from math import factorial n = int(input()) print([int(factorial(n) / (factorial(j) * factorial(n - j))) for j in range(n + 1)]) 

l = [1] for _ in range(int(input())): l = [a + b for a, b in zip([*l, 0], [0, *l])] print(l) 

import math def fac(num): return math.factorial(num) def pasc(n): row = [1] for i in range(1, n + 1): row.append(int(fac(n) / (fac(i) * fac(n - i)))) return row n = int(input()) print(pasc(n)) 

Материалы по теме

Источник