What is load factor in java

HashMap Load Factor

HashMap is one of the most high performing class in java collection framework. HashMap almost gives constant time performance for any size of data for frequent operations – insert and retrieve. It is very popular data structure and found useful for solving many problems due to O(1) time complexity for both insert and retrieve operation. This is the main reason why HashMap is considered for the heavy sized data and it will still provide faster insertion and retrieval operations.

There are mainly two factors which affect the performance of HashMap.

These two factors plays important role in performance of HashMap so these should be chosen very carefully while constructing an HashMap object.

Before proceeding further, It is important to understand the HashMap in depth. So please go through the below link :

HashMap Initial Capacity

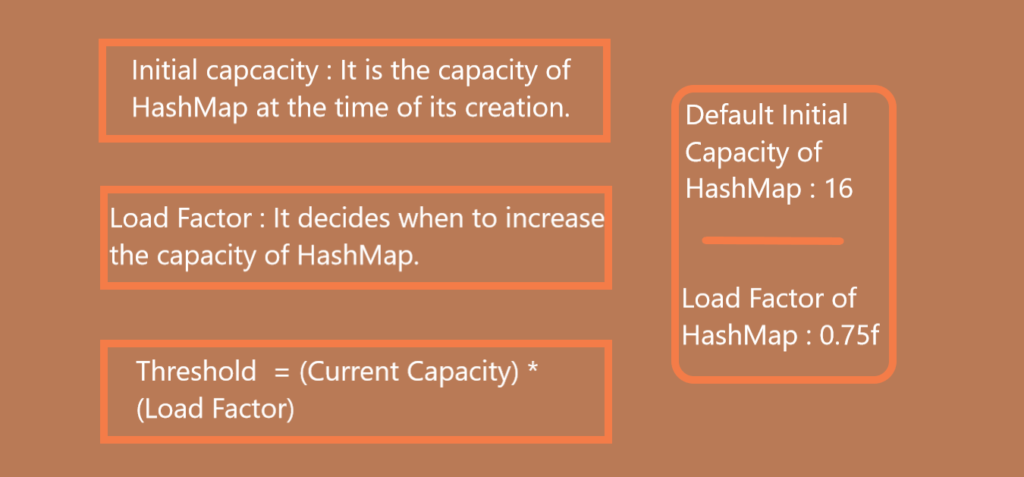
As we know, HashMap uses hash table as its underlying data structure. The capacity of an HashMap is the number of buckets present in the hash table. The initial capacity is the capacity of an HashMap at the time of its creation.

The default initial capacity of the HashMap is 2 4 i.e 16.

The capacity of the HashMap is doubled each time as it reaches the threshold. i.e the capacity is increased to 2 5 =32, 2 6 =64, 2 7 =128….. when the threshold is reached.

HashMap Load Factor

Load Factor is a measure which decides when to increase the hashmap capacity i.e buckets to maintain insert and retrieve operation complexity as O(1).

When the total number of items in hashmap goes on increasing keeping the default initial capacity of hashmap 16, At one point of time, hashmap performance will start degrading and need to increase buckets for improving performance.

The default load factor of HashMap is 0.75f.

HashMap Threshold Calculation

The threshold of an HashMap is calculated with the product of current capacity and load factor.

Threshold = (Current Capacity) * (Load Factor)

For example, if HashMap object is created with initial capacity of 16 then :

As we know, HashMap Load Factor is 0.75.

That means, the capacity of the HashMap is increased from 16 to 32 after the 12th element (key-value pair) is added into the HashMap object.

How Initial Capacity And Load Factor plays important role in Performance Of HashMap

Internally, Rehashing is done whenever HashMap reaches its threshold.

Rehashing is the procedure where a new HashMap object with a new capacity is created and all the old elements are placed into new object after re-calculating their hashcodes.

The process of re-hashing is costly as it is both time and space consuming so it affects the HashMap performance.

To maintain the performance, the initial capacity should be chosen very carefully. Initial capacity should be decided by keeping number of expected elements in mind. We should ensure that rehashing does not occur frequently.

You have to be very careful while choosing the load factor of HashMap too. According to Oracle doc, the default load factor of 0.75f always gives best performance in terms of both time and space.

For example :

If you choose HashMap load factor as 1.0f.

Threshold = 16 * 1.0 = 16;

It means, rehashing takes place after filling 100% of the current capacity.

This may save the space but it will increase the retrieval time of existing elements.

Suppose if you choose load factor as 0.5f, then rehashing takes place after filling 50% of the current capacity. This will increase the number of rehashing operations. This will further degrade the performance of HashMap in terms of both time and space.

So, you have to be very careful while choosing the initial capacity and load factor of an HashMap object. Choose the initial capacity and load factor such that they minimize the number of rehashing operations.

Conclusion

Congratulations Readers! In this article you have learnt the Load Factor of HashMap, Initial Capacity of HashMap, How these are important for performance of HashMap and What is the Rehashing process.

Источник

Load Factor in HashMap in Java with Examples

HashMap is a class that implements the Map interface of Java Collections Framework. The most important feature of a HashMap is that it has a constant time performance for retrieval and insertion. The two factors that dictate the performance of a HashMap are:

Before we explain what is the Load Factor of a HashMap, it is essential to understand its structure.

A HashMap has nodes that contain the key value pair much like a node in a Map. HashMap has buckets that contain the nodes, a bucket may contain more than one node. The basic structure of a HashMap is as follows:

Schematic of the structure of HashMap

Index: It is the integer value obtained after performing bitwise AND operation on the value of hash of the key and array size minus one.

where hashcode is a predefined function that returns the integer value of the hash of the key and ArraySize is the number of buckets in the HashMap.

Bucket: It is a LinkedList structure of nodes.

Node: It is the elementary unit of a HashMap. It contains the key-value pair and a link to the next node.

The syntax to declare a HashMap object is as follows:

HashMap objectName = new HashMap(int initialCapacity, float loadFactor)

Initial Capacity

The Initial Capacity is essentially the number of buckets in the HashMap which by default is 2 4 = 16. A good HashMap algorithm will distribute an equal number of elements to all the buckets.

Say we have 16 elements then each bucket will have 1 node, the search for any element will be achieved with 1 lookup. If we have 32 elements then each bucket will have 2 nodes, the search for any element will be achieved with 2 lookups. Similarly, if we have 64 elements then each bucket will have 4 nodes, the search for any element will be achieved with 4 lookups and so on.

As you can observe when the number of elements doubles the number of lookup increment by 1, which is good for the performance.

But what happens when the number of elements goes to a very high value, say 10,000, in that case, we will require 625 lookups. Similarly, if the number of elements is 10,00,000 we will require 62,500 lookups. Such a high number of lookups will degrade the performance of the HashMap. This is where the Load Factor comes into play.

Load Factor

The Load Factor is a threshold, if the ratio of the current element by initial capacity crosses this threshold then the capacity increases so that the operational complexity of the HashMap remains O(1). The meaning of operational complexity of O(1) means the retrieval and insertion operations take constant time.
The default load factor of a HashMap is 0.75f.

How do we decide when to increase the capacity?

Let us take an example, since the initial capacity by default is 16, consider we have 16 buckets right now.

We insert the first element, the current load factor will be 1/16 = 0.0625. Check is 0.0625 > 0.75 ? The answer is No, therefore we don’t increase the capacity.

Next we insert the second element, the current load factor will be 2/16 = 0.125. Check is 0.125 > 0.75 ? The answer is No, therefore we don’t increase the capacity.

Similarly, for 3rd element, load factor = 3/16 = 0.1875 is not greater than 0.75, No change in the capacity.

4th element, load factor = 4/16 = 0.25 is not greater than 0.75, No change in the capacity.

5th element, load factor = 5/16 = 0.3125 is not greater than 0.75, No change in the capacity.

6th element, load factor = 6/16 = 0.375 is not greater than 0.75, No change in the capacity.

7th element, load factor = 7/16 = 0.4375 is not greater than 0.75, No change in the capacity.

8th element, load factor = 8/16 = 0.5 is not greater than 0.75, No change in the capacity.

9th element, load factor = 9/16 = 0.5625 is not greater than 0.75, No change in the capacity.

10th element, load factor = 10/16 = 0.625 is not greater than 0.75, No change in the capacity.

11th element, load factor = 11/16 = 0.6875 is not greater than 0.75, No change in the capacity.

12th element, load factor = 12/16 = 0.75 is equal to 0.75, still No change in the capacity.

13th element, load factor = 13/16 = 0.8125 is greater than 0.75, at the insertion of the 13th element we double the capacity.

Now the capacity is 32.

In a similar way, every time an insertion crosses the load factor of 0.75 the capacity is doubled for a constant time performance of get() < retrieval >and put() < insertion >operations.

Solve DSA problems on GfG Practice.

Источник

Load Factor and Rehashing

Rehashing is the process of increasing the size of a hashmap and redistributing the elements to new buckets based on their new hash values. It is done to improve the performance of the hashmap and to prevent collisions caused by a high load factor.

When a hashmap becomes full, the load factor (i.e., the ratio of the number of elements to the number of buckets) increases. As the load factor increases, the number of collisions also increases, which can lead to poor performance. To avoid this, the hashmap can be resized and the elements can be rehashed to new buckets, which decreases the load factor and reduces the number of collisions.

During rehashing, all elements of the hashmap are iterated and their new bucket positions are calculated using the new hash function that corresponds to the new size of the hashmap. This process can be time-consuming but it is necessary to maintain the efficiency of the hashmap.

Why rehashing?
Rehashing is needed in a hashmap to prevent collision and to maintain the efficiency of the data structure.

As elements are inserted into a hashmap, the load factor (i.e., the ratio of the number of elements to the number of buckets) increases. If the load factor exceeds a certain threshold (often set to 0.75), the hashmap becomes inefficient as the number of collisions increases. To avoid this, the hashmap can be resized and the elements can be rehashed to new buckets, which decreases the load factor and reduces the number of collisions. This process is known as rehashing.

Rehashing can be costly in terms of time and space, but it is necessary to maintain the efficiency of the hashmap.

How Rehashing is done?
Rehashing can be done as follows:

• For each addition of a new entry to the map, check the load factor.
• If it’s greater than its pre-defined value (or default value of 0.75 if not given), then Rehash.
• For Rehash, make a new array of double the previous size and make it the new bucketarray.
• Then traverse to each element in the old bucketArray and call the insert() for each so as to insert it into the new larger bucket array.

Program to implement Rehashing:

C++

Java

Python3

C#

Javascript

HashMap created Number of pairs in the Map: 0 Size of Map: 5 Default Load Factor : 0.75 Pair(1, Geeks) inserted successfully. Current Load factor = 0.2 Number of pairs in the Map: 1 Size of Map: 5 Current HashMap: key = 1, val = Geeks Pair(2, forGeeks) inserted successfully. Current Load factor = 0.4 Number of pairs in the Map: 2 Size of Map: 5 Current HashMap: key = 1, val = Geeks key = 2, val = forGeeks Pair(3, A) inserted successfully. Current Load factor = 0.6 Number of pairs in the Map: 3 Size of Map: 5 Current HashMap: key = 1, val = Geeks key = 2, val = forGeeks key = 3, val = A Pair(4, Computer) inserted successfully. Current Load factor = 0.8 0.8 is greater than 0.75 Therefore Rehashing will be done. ***Rehashing Started*** Pair(1, Geeks) inserted successfully. Current Load factor = 0.1 Number of pairs in the Map: 1 Size of Map: 10 Pair(2, forGeeks) inserted successfully. Current Load factor = 0.2 Number of pairs in the Map: 2 Size of Map: 10 Pair(3, A) inserted successfully. Current Load factor = 0.3 Number of pairs in the Map: 3 Size of Map: 10 Pair(4, Computer) inserted successfully. Current Load factor = 0.4 Number of pairs in the Map: 4 Size of Map: 10 ***Rehashing Ended*** New Size of Map: 10 Number of pairs in the Map: 4 Size of Map: 10 Current HashMap: key = 1, val = Geeks key = 2, val = forGeeks key = 3, val = A key = 4, val = Computer Pair(5, Portal) inserted successfully. Current Load factor = 0.5 Number of pairs in the Map: 5 Size of Map: 10 Current HashMap: key = 1, val = Geeks key = 2, val = forGeeks key = 3, val = A key = 4, val = Computer key = 5, val = Portal

The time complexity of the insert operation is O(1) and the
Auxiliary space : O(n).

The time complexity of the rehash operation is O(n) and the
Auxiliary space: O(n).

Solve DSA problems on GfG Practice.

Источник