- Binary Search in Java Programming
- What is Binary Search in Java?
- Binary Search Visualization
- Algorithm for Binary Search
- Java Program for Binary Search
- Binary Search when array is in ascending order
- Output
- Binary Search when array is in descending order
- Output
- Binary Search Program Explanation
- Explanation
- Binary Search in Java – Algorithm Example
- How Does the Binary Search Algorithm Work?
- Step #1 - Sort the Array
- Step #2 - Choose Low and High Values
- Step #3 - Choose Midpoint/Middle Element
- Step #4 - Binary Search
- Iteration #1
- Iteration #2
- Binary Search Algorithm Example in Java
- Differences Between Binary Search Algorithm and Binary Search Tree
- Summary
- What is binary search in java
- Comparison with other Searching
- Some problems on Binary Search
- Variants of Binary Search
- Comparison with other Searching
- Some problems on Binary Search
Binary Search in Java Programming
In this lesson, we will understand what is Binary Search in Java Programming along with some examples.
What is Binary Search in Java?
A Binary Search is a searching technique used in java to search an element from an array. Binary search only works on sorted arrays.
Suppose we have a sorted array in ascending order, and we are looking for an element in the array, which is situated, at the end of the array. In this case, linear search is not suitable because it will scan each element from the start until it reached the last element that we are searching for in the array. In this situation, Binary Search is a more suitable and efficient searching technique compare to Linear Search.
In this searching technique, we compare the search element with the middle element of the array. If the search element is greater than the middle element, then we start searching in the right portion of the array after the middle element. If the search element is less then the middle element, then we start searching in the left portion of the array below the middle element. Now we will take only that portion in which the search element may be present and again compare the search element with the middle element of that portion. This process will be in iteration until we find the element, or there is no left or right portion left to search the element.
To clearly understand the binary search technique, let’s go through its algorithm step by step with an example.
Binary Search Visualization
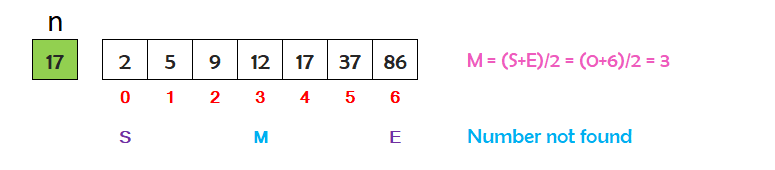
Suppose we have seven numbers stored in ascending order in an array as shown below. We want to search the number 17 in the array.
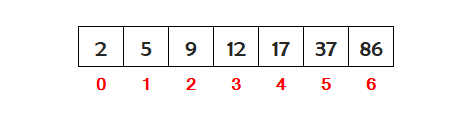
n is a variable that contains the number 17 we want to search in the array.
S is a variable stands for start index and contains the index 0.
E is a variable stands for end index and contains the index 6.
M is a variable stands for middle index and contains the index (S+E)/2=3.
The value of n=17 is not matching with the middle index value 12. The value of n is greater then the middle index value. So we will search in the right portion of the array starting after the middle index.
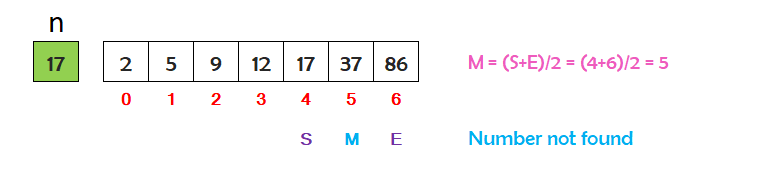
Now the value of S will be M+1=4.
The value of E remains the same, that is 6.
The value of M will be (S+E)/2=5.
The value of n=17 is not matching with the middle index value 37. The value of n is smaller then the middle index value. So we will search in the left portion of the array below the middle index.
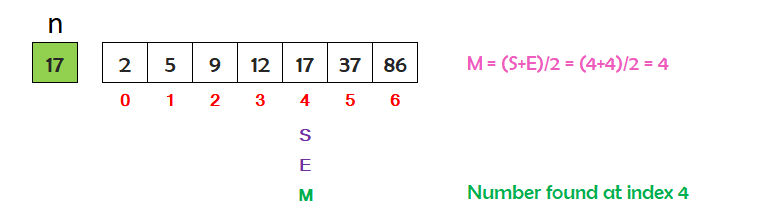
The value of S remains same, that is 4.
Now the value of E will be M-1=4.
The value of M will be (S+E)/2=4.
Now the value of n=17 is matching with the middle index value 17. So, the search is successful and the element is found at index 4.
Algorithm for Binary Search
An algorithm is the steps used to implement the binary search in a java program.
Assume we have N numbers in ascending order, stored in an array. To implement the binary search on N numbers, the steps are as follows.
- Define an array to store N numbers in ascending order for binary search. Suppose we have defined an array with the name num.
- Store the number we want to search in a variable say x.
- Declare a variable f and set its value 0. For example f=0.
- Set the value of the start index variable S=0 and end index variable E=N-1.
- Run a while loop i till S.
- Find the middle index M by dividing the sum of S and E by 2 and consider only the integer part of the result.
- Check if value of x is equal to the value of num[M] then print message Number found at index along with the value of M and set f=1 and then break the loop.
- Check If value of x is greater than the value at num[M] then set the start index S=M+1.
- If value of x is smaller than the value at num[M] then set the end index E=M-1.
- Outside the body of the loop i check if value of f is 0 then print the message Number not found.
Java Program for Binary Search
A Java program to search a number in an array having numbers in ascending order using binary search technique.
Binary Search when array is in ascending order
import java.util.Scanner; public class BinarySearchAscending < public static void main(String args[]) < // define an array that contain numbers in ascending order int num[]= ; int i,x,f,S,E,M; Scanner sc=new Scanner(System.in); System.out.print("Array: "); for(i=0; i // store the number in variable x to search in the array System.out.print("\n\nEnter number to search "); x=sc.nextInt(); // set the value of variable f=0 f=0; // set the start index S, end index E with the start and end index of the array S=0; E=num.length-1; // run a while loop till S is less than or equal to E while(S <=E) < // find the middle index M by dividing the sum of S and E by 2 // and consider only the integer part of the result. M=(S+E)/2; // check if value of x is equal to the value of num[M] then print message // 'Number found at index' along with the value of M and set f=1 and then break the loop if(x==num[M]) < System.out.print("Number found at index "+M); f=1; break; >else if(x>num[M]) // check if value of x is greater than the value at num[M] then set the start index S=M+1 < S=M+1; >else if(x > // check if value of f is 0 then print number not found if(f==0) < System.out.print("Number not found"); >> > Output
Array: 2 5 9 12 17 37 86 Enter number to search 17 Number found at index 4
A Java program to search a number in an array having numbers in descending order using binary search technique.
Binary Search when array is in descending order
import java.util.Scanner; public class BinarySearchDescending < public static void main(String args[]) < // define an array that contain numbers in ascending order int num[]= ; int i,x,f,S,E,M; Scanner sc=new Scanner(System.in); System.out.print("Array: "); for(i=0; i // store the number in variable x to search in the array System.out.print("\n\nEnter number to search "); x=sc.nextInt(); // set the value of variable f=0 f=0; // set the start index S, end index E with the start and end index of the array S=0; E=num.length-1; // run a while loop till S is less than or equal to E while(S <=E) < // find the middle index M by dividing the sum of S and E by 2 // and consider only the integer part of the result. M=(S+E)/2; // check if value of x is equal to the value of num[M] then print message // 'Number found at index' along with the value of M and set f=1 and then break the loop if(x==num[M]) < System.out.print("Number found at index "+M); f=1; break; >else if(x>num[M]) // check if value of x is greater than the value at num[M] then set the end index E=M-1 < E=M-1; >else if(x > // check if value of f is 0 then print number not found if(f==0) < System.out.print("Number not found"); >> > Output
Array: 86 37 17 12 9 5 2 Enter number to search 17 Number found at index 2
Binary Search Program Explanation
The explanation of the above program is given below in details.
Explanation
Array: 2 5 9 12 17 37 86 x = 17 Number to be search in the array f = 0 S = 0 Start index E = 6 End index Running a while loop i till SFor over a decade, Dremendo has been recognized for providing quality education. We proudly introduce our newly open online learning platform, which offers free access to popular computer courses.
Our Courses
News Updates
Do you like cookies? 🍪 We use cookies to ensure you get the best experience on our website. Learn more I agree
Binary Search in Java – Algorithm Example
Ihechikara Vincent Abba
Algorithms provide step by step instructions on solving specific problems. They help you solve problems using efficient, standard, and reusable steps.
The binary search algorithm is one of the commonly used algorithms in programming. It is used to search and find an element in a sorted array.
The binary search algorithm is different from the binary search tree. We'll talk about their differences later in this article.
In this article, you'll learn how the binary search algorithm works with the aid of diagrams and code examples.
You'll see how to implement the algorithm in your Java program.
How Does the Binary Search Algorithm Work?
In this section, you'll see a practical application of binary search using diagrams.
The binary search algorithm is a divide and conquer algorithm that searches for a specific element in a sorted array.
Note that the collection of elements/array must be sorted for the algorithm to work efficiently.
Here are the steps involved with the binary search algorithm:
Step #1 - Sort the Array
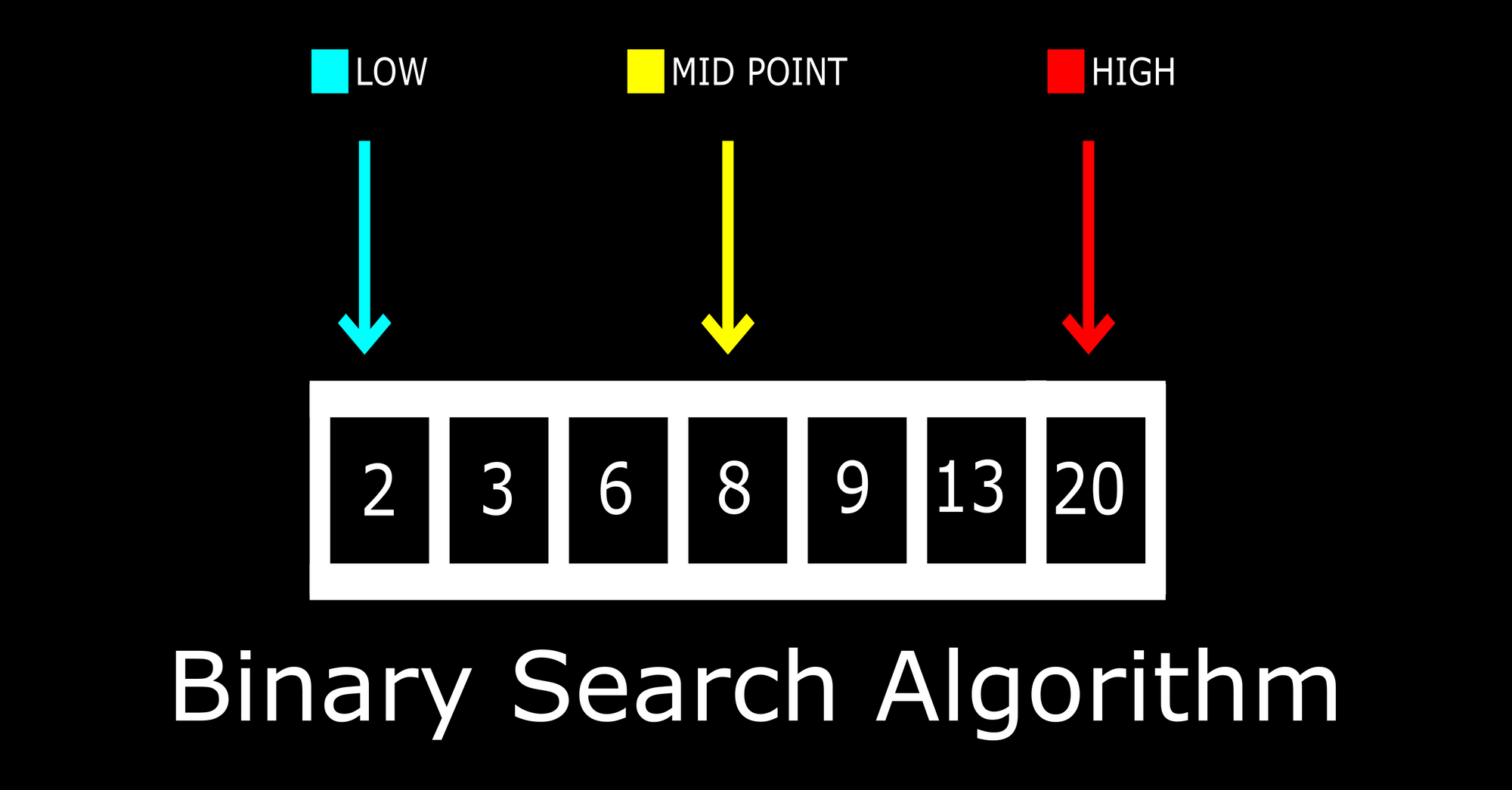
In order to start the search, you'll need to have a sorted array. The image above has a collection of numbers sorted in ascending order: 2,3,6,8,9,13,20.
Let's assume that the element we're looking for is 13. We'll store this in a variable called number_to_search_for .
Step #2 - Choose Low and High Values
The first index of the array will be denoted as low while the highest index will be denoted as high .
These values will help you get the midpoint of the array.
Step #3 - Choose Midpoint/Middle Element
The image above shows the midpoint which is at the center of the array.
Now that you know the low , high , and midpoint of the array, the binary search operation can begin.
Step #4 - Binary Search
This is what happens during the binary search:
- If number_to_search_for is equal to midpoint , the midpoint index will be returned.
- If number_to_search_for is greater than midpoint , search through the elements on the right side of the midpoint .
- If number_to_search_for is less than midpoint , search through the elements on the left side midpoint .
Step 3 will only be relevant if step 2 is false. If number_to_search_for doesn't exist in the array, return -1.
Let's simplify the steps above using diagrams:
This is the array we're working with: 2,3,6,8,9,13,20.
Iteration #1
From the steps listed above, you begin by comparing number_to_search_for to midpoint .
As you can see in the diagram above, the value of number_to_search_for and midpoint are not the same.
The next step is to find out if the number_to_search_for is greater than or less than midpoint .
In our own case, it is greater than midpoint so we'll focus on the elements on the right side of the midpoint — 9, 13, and 20.
This makes the search much faster because we've cut out half of the array that isn't needed.
We'll repeat all the steps for those elements as well.
The steps will run continuously until the element is found. In a case where the element doesn't exist, -1 will be returned.
Iteration #2
Comparing the midpoint and number_to_search_for in the diagram above, we have the same value.
At this point, the binary search operation stops because we've found the number. The index of the number will be returned.
That is: index 5 from the original array (2,3,6,8,9,13,20).
In the next section, you'll see how to implement the algorithm in Java.
Binary Search Algorithm Example in Java
class BinarySearch < private static int binarySearch(int numArray[], int number_to_search_for) < int low = 0; int high = numArray.length - 1; while (low if (number_to_search_for < middleIndexNumber)< high = middleIndex - 1; >if (number_to_search_for > middleIndexNumber) < low = middleIndex + 1; >> return -1; > public static void main(String args[]) < int[] arrayofnums = ; System.out.println(binarySearch(arrayofnums, 13)); // 5 > >In the code above, we created a method called binarySearch with two parameters — int numArray[] and int number_to_search_for :
private static int binarySearch(int numArray[], int number_to_search_for)The first parameter represents the array to be searched through. The second represents the number to be searched for.
Next, we defined the low and high variables to represent the first and last index of the array:
int low = 0; int high = numArray.length - 1;After that, we created a while loop with if statements matching the 3 steps used in the previous section (Step #4 - Binary Search section):
while (low if (number_to_search_for < middleIndexNumber)< high = middleIndex - 1; >if (number_to_search_for > middleIndexNumber) < low = middleIndex + 1; >>You can have a look at the Step #4 - Binary Search section to understand the code in the while loop.
We then returned -1 after the while loop in case the number being searched for doesn't exist in the array.
Lastly, we tested the method to be sure the functionality worked as expected:
public static void main(String args[]) < int[] arrayofnums = ; System.out.println(binarySearch(arrayofnums, 13)); // 5 >We specified 13 as the second parameter and got index 5 returned.
If you use a number that doesn't exist in the array, you'll get -1 returned.
Differences Between Binary Search Algorithm and Binary Search Tree
Although both binary search algorithm and binary search tree are both used for searching, there are some differences in mode operation of operation and data structure.
Here are some differences:
- Binary search algorithm is used for searching while binary search tree is used for searching, insertion, and deletion.
- Binary search algorithm compares the middle element with the element being searched for while binary search tree compares the value of nodes in a tree.
- Binary search algorithm searches through an array or list while binary search tree traverses through a tree of nodes.
You can read more about the binary search tree here.
Summary
In this article, we talked about the binary search algorithm. It is to search for specific elements in an array.
We saw how the algorithm works using visual guides. Then we saw an implementation of the algorithm in Java.
Lastly, we saw the differences between binary search algorithm and binary search tree.
What is binary search in java
Comparison with other Searching
Some problems on Binary Search
- Check if an array is sorted and rotated using Binary Search
- Longest Common Prefix using Binary Search
- Find the Peak Element in a 2D Array/Matrix
- Search an element in a sorted and rotated array with duplicates
- Search for an element in a Mountain Array
- Median of two Sorted Arrays of Different Sizes
- Longest Increasing Subsequence Size (N log N)
- Median of two Sorted Arrays of Different Sizes using Binary Search
- The Painter’s Partition Problem using Binary Search
- Allocate Minimum Number of Pages from N books to M students
- Find largest median of a sub array with length at least K
Variants of Binary Search
Comparison with other Searching
Some problems on Binary Search
- Check if an array is sorted and rotated using Binary Search
- Longest Common Prefix using Binary Search
- Find the Peak Element in a 2D Array/Matrix
- Search an element in a sorted and rotated array with duplicates
- Search for an element in a Mountain Array
- Median of two Sorted Arrays of Different Sizes
- Longest Increasing Subsequence Size (N log N)
- Median of two Sorted Arrays of Different Sizes using Binary Search
- The Painter’s Partition Problem using Binary Search
- Allocate Minimum Number of Pages from N books to M students
- Find largest median of a sub array with length at least K