Вырожденность задачи линейного программирования

9.Вырожденность задач линейного программирования. Правило устранения зацикливания.

факт существования вырожденной системы может привести так называнию зацикливанию, когда должно произойти увеличение целевой функции при переходе к новому опорному плану, а увеличении не происходит.

Если при выборе разрешающего элемента оказалось несколько min отношений, то следует выбрать то элемент, для которого будет наименьшим отношение другого столбца к разрешающим элементам. Если опять будет альтернатива выбора, то составляем отношение элементов след столбца к разрш., до тех пор разр. элемент не будет выбран однозначно.

12. Двойственный симплекс-метод.

1. Приводим задачу к каноническому виду и приводим систему к ед базису (Ж-Г).+ свободные члены не обязательно
2. Переносим условия задачи в симплекс таблицу
3. Освобождаемся от отрицательных свободных членов, выбирая разрешающий элемент по следующиму правилу:

— рассмотрим строку с наибольшим по абсолютной величине отриц. Свободным членом и смотрим, есть ли отриц коэффициенты

-если нет, то задача не имеет решений

-если есть, то для столбцов, содержащих их, находим, наименьшее + отношение свободных членов к соответствующим элементам столбцов

-умножаем эти наименьшие отношения на соотв оценки индексной строки и выбираем min значение

— по выбранному произведению выбираем разрешающий элемент.

8.Симплекс-метод решения задач линейного программирования. Определение исходного опорного решения. Вторая часть симплекс-метода. Симплекс-таблицы.

Решение состоит из 2-х частей

1. Нахождение исходного опорного решения
2. Последовательный переход от полученного опорного решения к новому улучшенному опорному решению.

1. Часть

• Систему приводим к ед базису (Ж-Г)
• Если появились отрицательные свободные члены, то от них избавляются
• Систему снова приводят к ед базису с помощью симплекс преобразований
• Если существует хотя бы 1 отрицательный свободный член, то базисное решение не явл оптимальным:

— в системе приведенной к ед базису, среди отриц. Свободных членов выбираем наибольший по абсолютной величине и уравнение которое ему соотв * на (-1). Затем + почленно к тем уравнениям системы, в которых св члены отриц. В результате получаем преобразованную систему. В которой все свободные члены>=0, но нарушен ед базис:

• Выбираем уравнение в котором нет базисных переменных, смотрим есть ли в нем +коэффициенты(если есть, то берем 1 из них и столбец, содержащий этот коэфф берем за разрешающий)
• В разрешающею строку выбираем по наименьшему + отношению свободных членов к + элементам разрешающего столбца
• Разрешающий элемент принадлежит уравнению, где нет базисных переменных, после 1 шага симплексного преобразования система будет приведена к ед базису и получено опорное решение
• Разрешающий элемент не принадлежит уравнению, которое не содержит базисную переменную, но принадлежит уравнению где свободный член>0. Если мы сделаем шаг симплексного преобразования, то система будет приведена к ед базису. От этого шага поменяется только состав базисных переменных. В этом случае продолжаем работать с интерес нас уравнением, выбирая разрешающий элемент по нашему правилу, до тех пор, пока не придем к первому случаю, либо установим, что система несовместна
• Разрешающий элемент расположен не в интер нас уравнении, а в другом где свободный член =0. В этом случае, если провести итерацию симплекс преобразований, то свободный член в интер нас уравнении не изменится. В этом случае рекомендуется попробовать выбрать др разрешающий элемент и для которого будет выполнен 1 или 2 случай.

Источник

14 Вырожденность в задачах линейного программирования.

Задача линейного программирования является невырожденной если каждый опорный план содержит ровно m положительных компонент, где m – число ограничений в задаче. В вырожденном опорном плане число положительных компонент оказывается меньше числа ограничений: некоторые базисные переменные, соответствующие данному опорному плану, принимают нулевые значения.

Используя геометрическую интерпретацию для простейшего случая, когда n-m=2 (число небазисных переменных равно 2), легко отличить вырожденную задачу от невырожденной. В вырожденной задаче в одной вершине многогранника условий пересекается более двух прямых, описываемых уравнениями вида x_i =0 . Это значит, что одна или несколько сторон многоугольника условий стягиваются в точку.

Аналогично при n-m=3 в вырожденной задаче в одной вершине пересекается более 3-х плоскостей x_i =0.

Если задача линейного программирования оказывается вырожденной, то при плохом выборе вектора условий, выводимого из базиса, может возникнуть бесконечное движение по базисам одного и того же опорного плана. Так называемое явление зацикливания. Хотя в практических задачах линейного программирования зацикливание явление крайне редкое, возможность его не исключена.

Один из приемов борьбы с вырожденностью состоит в преобразовании задачи путем “незначительного” изменения вектора правых частей системы ограничений на величины , таким образом, чтобы задача стала невырожденной и, в то же время, чтобы это изменение не повлияло реально на оптимальный план задачи.

19.Оценки как мера дефицитности ресурсов в рентабельности отдельных видов продукции

Компоненты оптимального решения двойственной задачи называются оптимальными(двойственными) оценками исходно задачи, или объективно обусловленными оценками.

Компоненты оптимального решения исходной задачи I

Превышение затрат на ресурсы над ценой реализации

Компоненты оптимального решения двойственной задачи II

В таблице дополнительные переменные исходной задачи 1 , , , , представляющие согласно выражению:

— разность между запасами ресурсов Sl, S2, Sз, S4 и их потреблением, выражают остатки ресурсов, а дополнительные переменные двойст­венной задачи II , , представляющие в соответствии с выраже­нием:

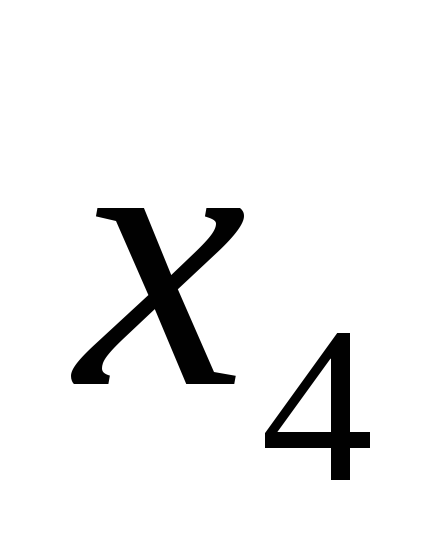
— разность между затратами на ресурсы для производст­ва из них единицы продукции и ценами С_j продукции P₁, Р₂, вы­ражают превышение затрат над ценой.

Ресурсы S1, S2 по оптимальному плану полностью использованы (), и объективно обусловленные оценки этих ресурсов ненулевые . Ресурсы S3, S4 не полностью используются в оптимальном плане и объек­тивно обусловленные оценки этих ресурсов нулевые .

Таким образом, объективно обусловленные оценки ресурсов оп­ределяют степень дефицитности ресурсов: по оптимальному пла­ну производства дефицитные (т.е. полностью используемые) ре­сурсы получают ненулевые оценки, а недефицитные — нулевые оценки.

Источник

2.8. Вырожденная задача лп

При использовании симплекс-метода некоторые свободные члены могут быть равны нулю. Это значит, что в вершине, которой соответствует CТ, равны нулю неkпеременных, а больше (равна нулю и базисная). В этом случае при выборе генерального элемента отношениеb_i/a_ijбудет минимальным именно для этой строки. Ясно, что соответствующую свободную переменную увеличить никак нельзя и целевая функция при переходе в новую вершину не меняется, т.к. мы остаемся фактически в этой же вершине, хотя формально перешли в новую..

Такая задача называется вырожденной задачей. Вырождение отрицательно сказывается на эффективности вычисления. Признаком вырожденности является равенство 0 некоторых свободных членов. В этом случае может произойти 2 отрицательных явления:

1. «Пробуксовка». Переходим в новую вершину, где равна нулю другая совокупность переменных, а на самом деле остаемся в той же точке. Значение ЦФ не меняется.
2. «Зацикливание» алгоритма. Через некоторое количество операций мы можем прийти к первоначальной таблице, следовательно, если алгоритм не менять, то зацикливаемся.

1. Использование степени свободы алгоритма. Например, если в алгоритме сказано: «берем первый по порядку…» — то, если обнаруживается зацикливание, можно взять «второй по порядку». Аналогично, если сказано «берем любой…».
2. «Зашумление» коэффициентов задачи ЛП. Прибавляем матрицу малых случайных величин к матрице А. Получаем А + ξ, где А – матрица коэффициентов; ξ – матрица очень малых случайных величин. Тогда матрица коэффициентов СТ не будет содержать одинаковых чисел и после вычислений появление нулей будет маловероятным. Подробнее этот сложный вопрос освещен в специальной литературе.

2.9. Двойственная задача лп

Важным вопросом анализа полученного решения ЛП является анализ чувствительности решения к параметрам модели (коэффициентам целевой функции, свободным членам ограничений, коэффициентам а_ij). Теория этого вопроса тесно связана с так называемойдвойственной задачей ЛП. Двойственная задача ЛП получается из прямой и она имеет физический смысл, когда прямая задача – задача об использовании ресурсов. Имеются ресурсыmтипов в колчествеb₁, … b_m. Для изготовления одного изделияj – го типа расходуетсяa_ijсырьяi-го типа. Каждое j– ое изделие продается по ценес_j. Ставится задача максимизации стоимости проданных изделий. (2.11) (2.12) Можно рассмотреть эту проблему по-другому. Пусть некоторые величины ∆_i– стоимости единицыi– го ресурса. Нужно определить эти стоимости так, чтобы выполнялись неравенства, выражающие то, что стоимость затраченного ресурса наj– е изделие была бы не меньше стоимости изделия и при этом общие затраты на ресурсы были минимальны. (2.13) _j=1,…n(2.14) Задача (2.13), (2.14) называется двойственной по отношению к задаче (2.11), (2.12) Она получается из прямой (2.11), (2.12) так: коэффициенты целевой функции двойственной задачи – это правые части прямой задачи и наоборот; а коэффициенты a_ij– суммируются по другому индексу (Матрица коэффициентов двойственной задачи это транспонированная матрица прямой задачи). Направление оптимизации целевой функции меняется на противоположное. Основное свойство задачи ЛП: оптимальное значение целевой функции прямой и двойственной задачи ЛП совпадают. Оптимальное решение задачи ЛП находится в седловой точке: maxL по х_j=min по ∆_i. Существует и двойственный симплекс – метод решения задачи ЛП, который в ряде случаев эффективнее прямого [1, 10]. Экономический смысл двойственной задачи: какова цена единицы каждого ресурса ∆_i, чтобы при заданных количествах ресурсовb_iи стоимости единицы продукции с_jобеспечит минимум общей стоимости затрат. ∆_iназываетсядвойственной оценкойилитеневой ценой. Если решение прямой найдено, то ∆_i– есть коэффициенты, стоящие с трокеLв последней оптимальнойCТ. Если ∆_i> 0, то она показывает насколько увеличивается значение целевой функции прямой задачи, если соответствующие запасы сырьяi– го типа увеличиваются на единицу. Соответствующая дополнительная переменная y_iпри этом равна нулю. Это означает, чтоi– ое ограничение выполняется точно (как равенство) и весь ресурсb_i тратится полностью. При малом изменении коэффициентов модели оптимальное решение задачи ЛП не меняется, такое свойство называетсяустойчивостью. На рисунке показано, что для ЦФ1 решением является точка А, для ЦФ3 *(при малом изменении коэффициентовc_jтакже- точка А, а для ЦФ2 решением уже будет точка В. Существуют специальные программы, которые позволяют проанализировать пределы изменения коэффициентов c_j, при которых оптимальное решение не изменяется, а значение целевой функции меняется. Аналогично проводится анализ по правым частям . Современные алгоритмы ЛП способны с использованием современных компьютеров решать задачи ЛП очень большой размерности. Многие из них учитывают архитектуру компьютера. Наиболее широко известны блочные методы ЛП. При большой размерности матрица А будет содержать много нулей. В этом случае задачу можно решать по блокам. Вот почему параметрами сложности решаемой задачи ЛП являются: число переменных,число ограниченийичисло ненулевых коэффициентовограничений. Число итераций симплекс- метода, за которое находится решение в большей степени зависит от числа ограничений. Современные программы ЛП имеют удобный интерфейс, позволяющий моделировать и решать небольшие задачи в удобной «математической» или табличной форме. Для решения задач ЛП большой размерности используются режимы работы с крупными базами исходных данных. (Смотри программыLINDO, а также приложение «Поиск решения» (SOLVER) программыMicrosoftEXCEL.

Источник