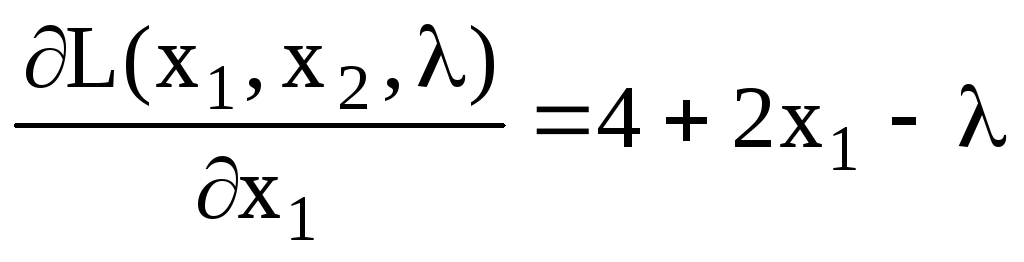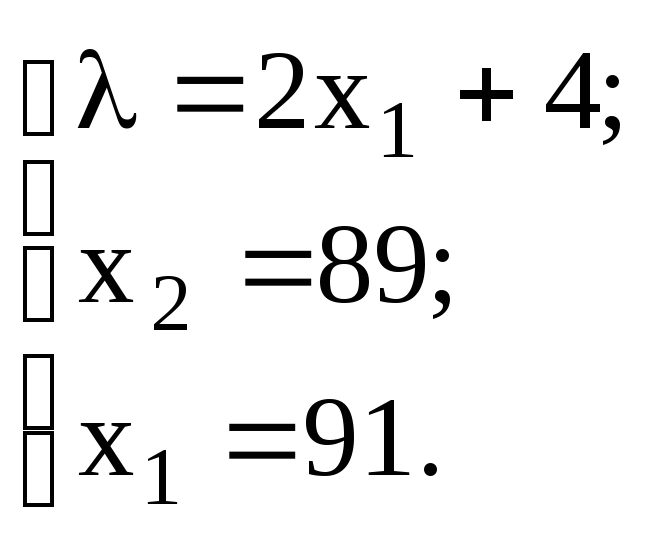Тема 10. Элементы нелинейного программирования
Для ЗНП, в отличие от ЗЛП, нет единого метода решения. В зависимости от вида целевой функции и ограничений разработано несколько специальных методов решения, к которым относятся методы множителей Лагранжа, квадратичное и выпуклое программирование, градиентные методы, ряд приближенных методов решения, графический метод.
2. Метод множителей Лагранжа
Пусть требуется решить ЗНП следующего вида
где и (или) непрерывны и дифференцируемы.
Для решения задачи вводят так называемую функцию Лагранжа L(x, l):
Метод функции Лагранжа сводит ЗНП на условный экстремум к задаче нахождения локального экстремума.
1) Составляют функцию Лагранжа.
2) Находят стационарные точки функции Лагранжа из системы уравнений:
3) Из найденных стационарных точек выбирают те, в которых функция L(x, l) имеет локальные экстремумы. Функция L(x, l) имеет в стационарной точке локальный максимум, если в ней дифференциал второго порядка меньшего нуля (d 2 L), и локальный минимум, если дифференциал второго порядка больше нуля (d 2 L>0).
Множителям Лагранжа можно придать экономический смысл. Если F(x1,x2…xn) – доход, соответствующий плану x=(x1,x2…xn), – затраты некоторых ресурсов, тогда множители будут показывать как изменится максимальный доход, если количество ресурса i-го вида увеличится на единицу.
Задача. Найти условный минимум функции при ограничениях
Составим функцию Лагранжа:
Найдем стационарные точки функции Лагранжа из системы уравнений:
Запишем дифференциал второго порядка функции Лагранжа. Поскольку все частные производные второго порядка, в записи которых присутствуют , равны нулю, то формула дифференциала второго порядка для функции Лагранжа примет вид:
Следовательно, точка является точкой минимума функции . Найдем значение функции в данной точке:
3. Задача выпуклого программирования
Пусть дана система неравенств вида:
причем все функции являются выпуклыми на некотором выпуклом множестве М, а функция либо выпукла вверх (выпукла), либо выпукла вниз (вогнута) на множестве М. З ВП состоит в отыскании такого решения системы ограничений, при котором выпуклая функция достигает минимального значения, или вогнутая функция достигает максимального значения.
Определение 10.1. Точка (x*, λ*) называется седловой точкой функции Лагранжа, если n-мерная точка x* является точкой минимума функции L(x, λ*), а m-мерная точка λ* – точкой максимума функции L(x*, λ), так что x и λ выполняется неравенство:
Теорема 10.1. (Условие регулярности Слейтера) Множество Х допустимых решений ЗВП удовлетворяет условию регулярности Слейтера, если существует по крайне мере одно точка , такая что .
Теорема 10.2 (теорема Куна-Таккера). Чтобы точка x* была оптимальным решением ЗВП, множество допустимых решений которой обладают свойством регулярности Слейтера, необходимо и достаточно, чтобы существовала такая пара (x*, λ*), которая являлась бы седловой точкой функции Лагранжа данной ЗВП.
Замечание 10.1. Если ограничения задачи – линейные функции, то выполнение условия регулярности не требуется.
Для того чтобы найти седловые точки необходимо и достаточно составить систему:
3.10. Задача выпуклого программирования
Определение 1: Функция f(x), определенная на выпуклом множестве Х, называется выпуклой, если для любых точек 


.
Если в этом соотношении при 




Определение 2: Функция f(x), определенная на выпуклом множестве Х, называется вогнутой, если для любых точек 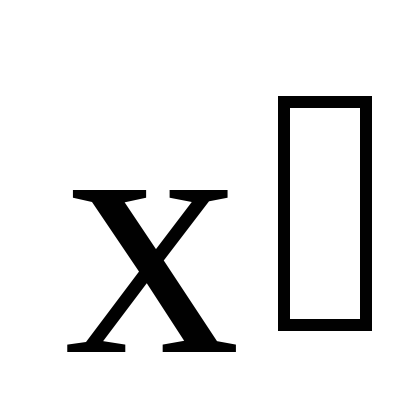


.
Если в этом соотношении при 




Определение 3: Задача математического программирования




в которой либо целевая функция, либо ограничения, либо то и другое нелинейны, называется нелинейной.
Класс задач нелинейного математического программирования очень велик. Общих универсальных методов нет. Однако, есть задачи нелинейного программирования, для которых есть методы решения. Один из таких типов задач являются задачи выпуклого программирования.
В теории выпуклого программирования в качестве основной обычно рассматривается задача минимизации выпуклой функции n переменных 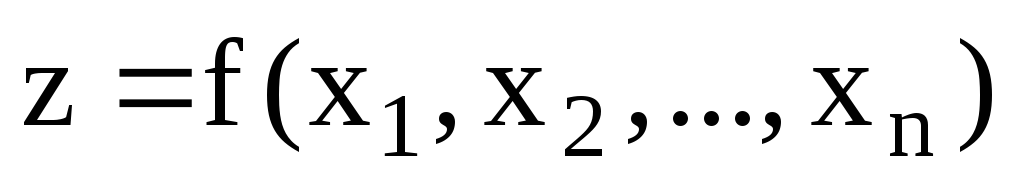
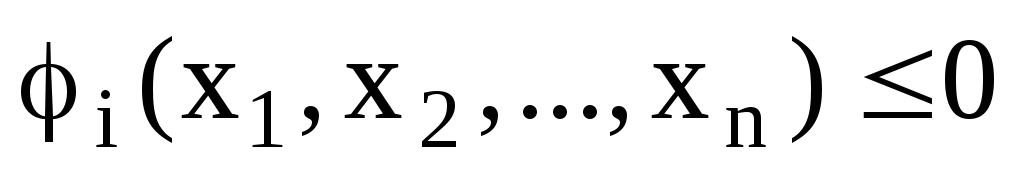
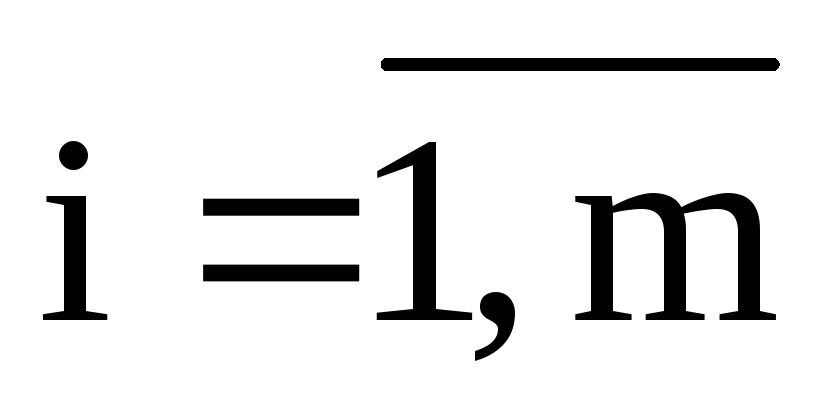
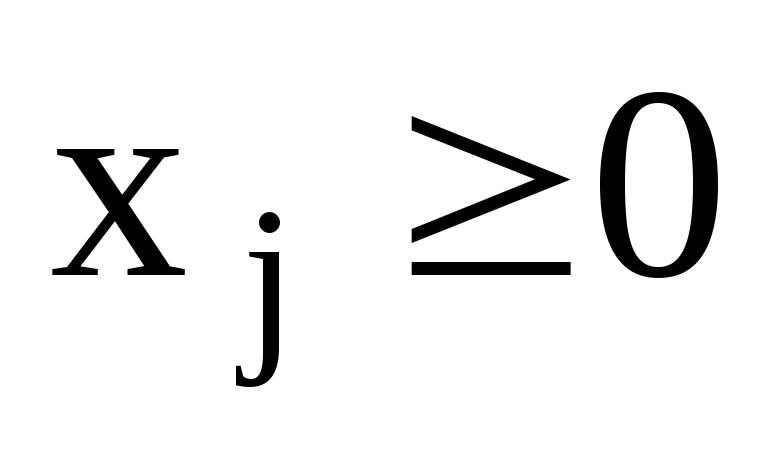

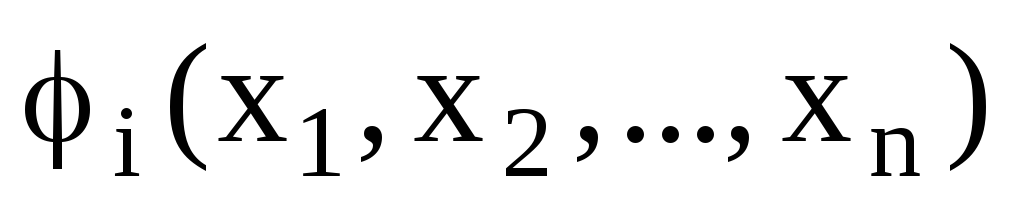
Если 


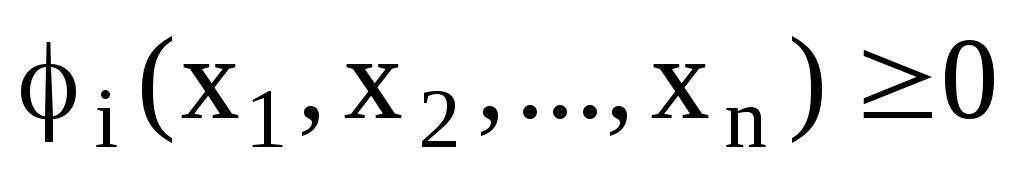



3.11. Метод множителей Лагранжа
Метод множителей Лагранжа является классическим методом решения задач математического программирования (в частности выпуклого).
Рассмотрим классическую задачу оптимизации

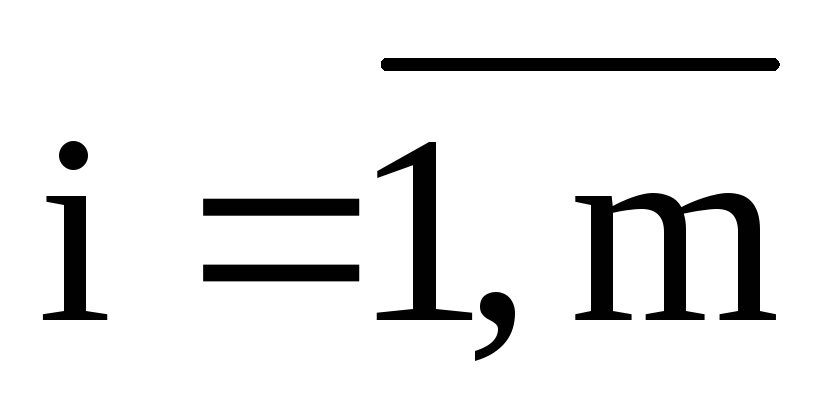
От основной задачи выпуклого программирования в данной постановке задача отличается тем, что в системе ограничений нет неравенств и нет ограничения неотрицательности для переменных.
Классический подход к решению данной задачи дает систему уравнений (необходимые условия), которым должна удовлетворять точка 
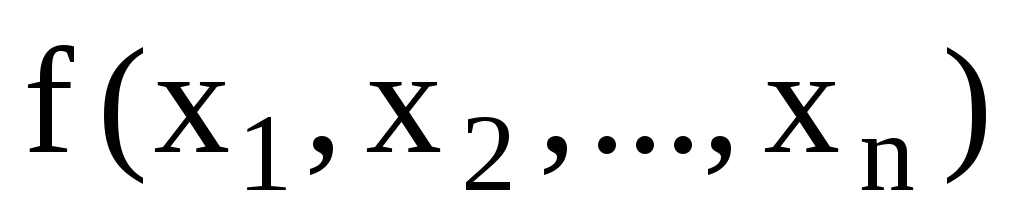
Предположим, что в точке 

равен m. Тогда необходимые условия запишутся в виде:



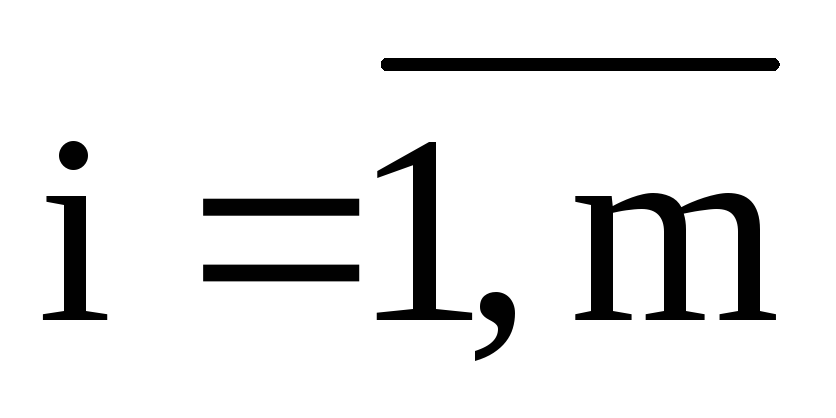
есть функция Лагранжа, – множители Лагранжа.
Алгоритм решения задачи методом множителей Лагранжа:
- Составить функцию Лагранжа.
- Найти частные производные функции Лагранжа по всем переменным
и приравнять их к нулю. Получим систему изn+m уравнений с n+m неизвестными. Решив полученную систему, вычислим стационарные токи функции Лагранжа.
- Из стационарных точек, взятых без
, выбрать точки, в которых функция имеет условный локальный экстремумы при наличии ограничений.
Пример: Решить задачу математического программирования, используя метод множителей Лагранжа. 
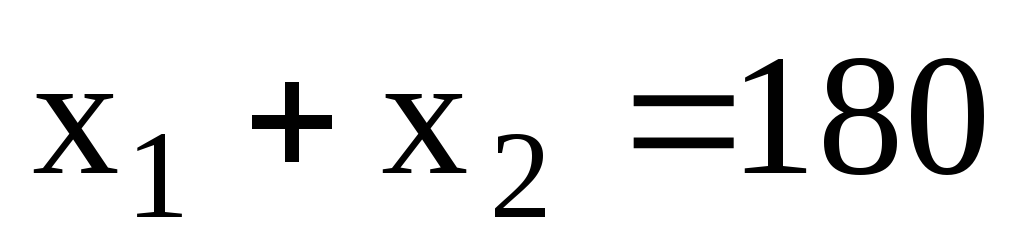




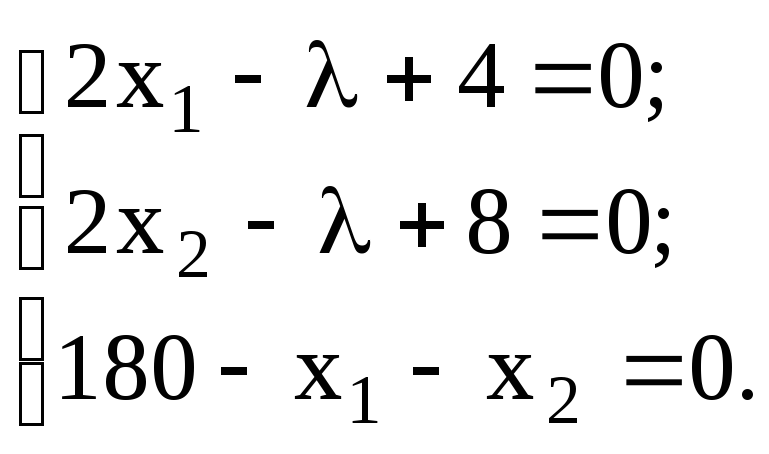
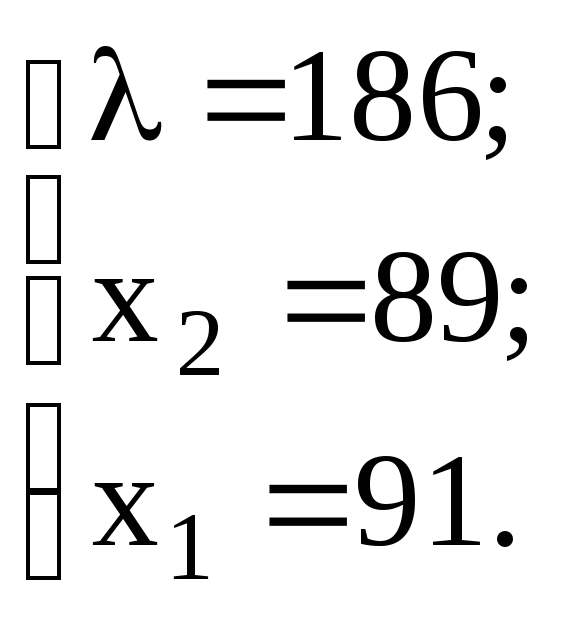
3.10. Задача выпуклого программирования
Определение 1: Функция f(x), определенная на выпуклом множестве Х, называется выпуклой, если для любых точек 


.
Если в этом соотношении при 
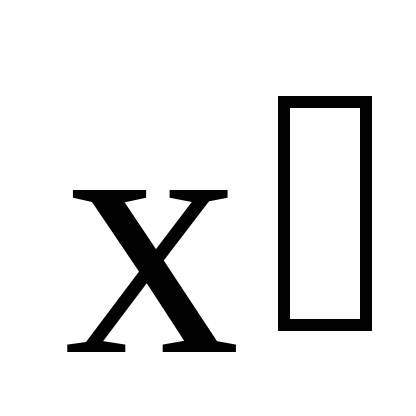



Определение 2: Функция f(x), определенная на выпуклом множестве Х, называется вогнутой, если для любых точек 

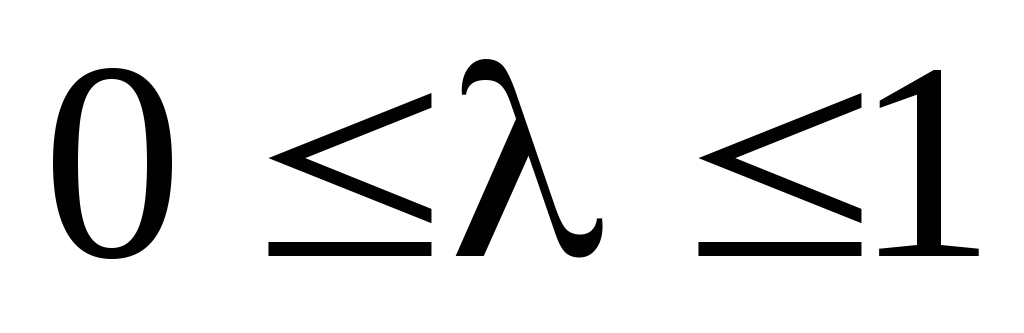
.
Если в этом соотношении при 
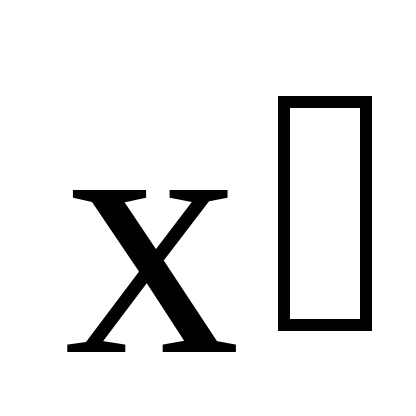



Определение 3: Задача математического программирования
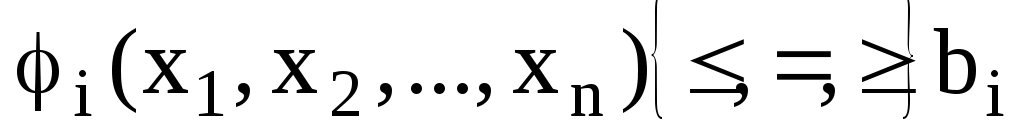



в которой либо целевая функция, либо ограничения, либо то и другое нелинейны, называется нелинейной.
Класс задач нелинейного математического программирования очень велик. Общих универсальных методов нет. Однако, есть задачи нелинейного программирования, для которых есть методы решения. Один из таких типов задач являются задачи выпуклого программирования.
В теории выпуклого программирования в качестве основной обычно рассматривается задача минимизации выпуклой функции n переменных 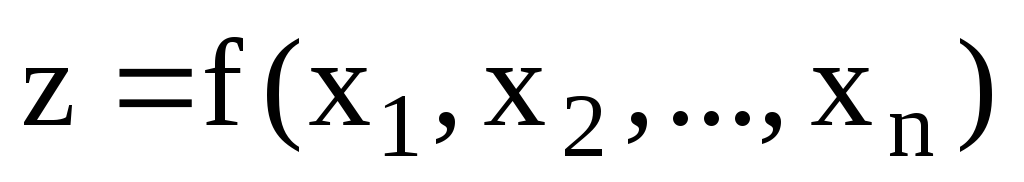





Если 






3.11. Метод множителей Лагранжа
Метод множителей Лагранжа является классическим методом решения задач математического программирования (в частности выпуклого).
Рассмотрим классическую задачу оптимизации


От основной задачи выпуклого программирования в данной постановке задача отличается тем, что в системе ограничений нет неравенств и нет ограничения неотрицательности для переменных.
Классический подход к решению данной задачи дает систему уравнений (необходимые условия), которым должна удовлетворять точка 

Предположим, что в точке 

равен m. Тогда необходимые условия запишутся в виде:




есть функция Лагранжа, – множители Лагранжа.
Алгоритм решения задачи методом множителей Лагранжа:
- Составить функцию Лагранжа.
- Найти частные производные функции Лагранжа по всем переменным
и приравнять их к нулю. Получим систему изn+m уравнений с n+m неизвестными. Решив полученную систему, вычислим стационарные токи функции Лагранжа.
- Из стационарных точек, взятых без
, выбрать точки, в которых функция имеет условный локальный экстремумы при наличии ограничений.
Пример: Решить задачу математического программирования, используя метод множителей Лагранжа. 



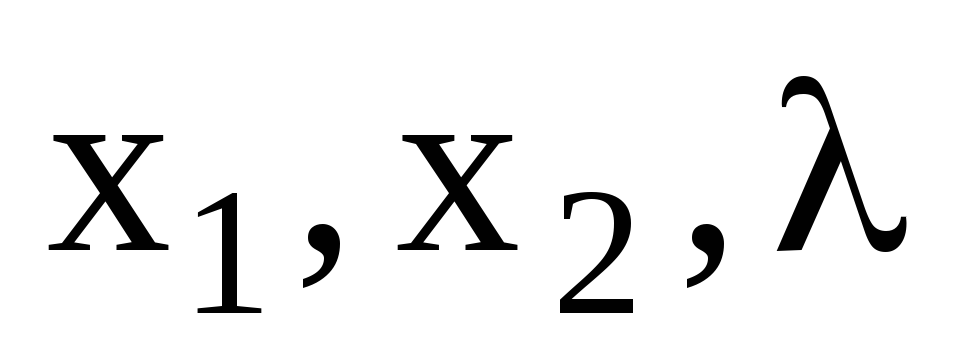








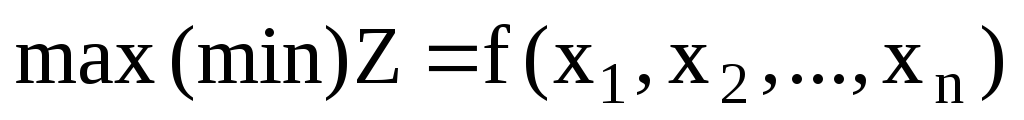




 и приравнять их к нулю. Получим систему изn+m уравнений с n+m неизвестными. Решив полученную систему, вычислим стационарные токи функции Лагранжа.
и приравнять их к нулю. Получим систему изn+m уравнений с n+m неизвестными. Решив полученную систему, вычислим стационарные токи функции Лагранжа.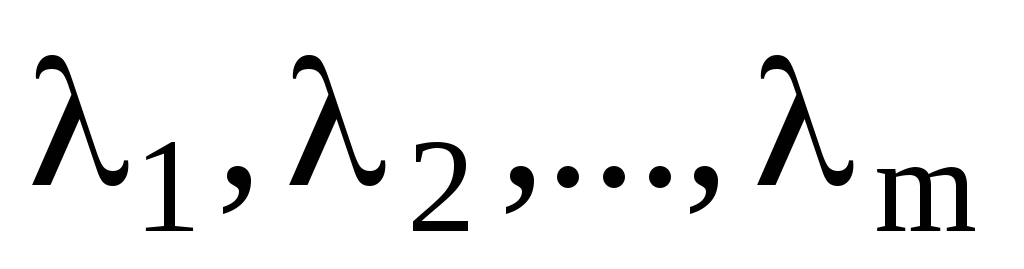 , выбрать точки, в которых функция имеет условный локальный экстремумы при наличии ограничений.
, выбрать точки, в которых функция имеет условный локальный экстремумы при наличии ограничений.










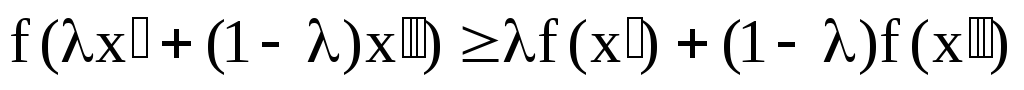







 и приравнять их к нулю. Получим систему изn+m уравнений с n+m неизвестными. Решив полученную систему, вычислим стационарные токи функции Лагранжа.
и приравнять их к нулю. Получим систему изn+m уравнений с n+m неизвестными. Решив полученную систему, вычислим стационарные токи функции Лагранжа. , выбрать точки, в которых функция имеет условный локальный экстремумы при наличии ограничений.
, выбрать точки, в которых функция имеет условный локальный экстремумы при наличии ограничений.