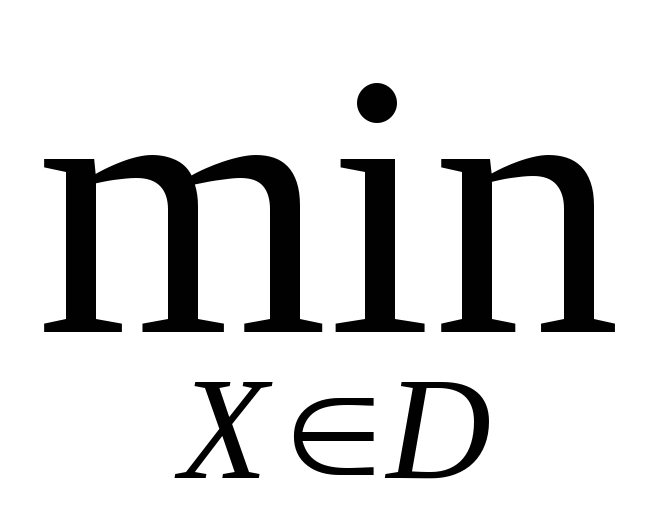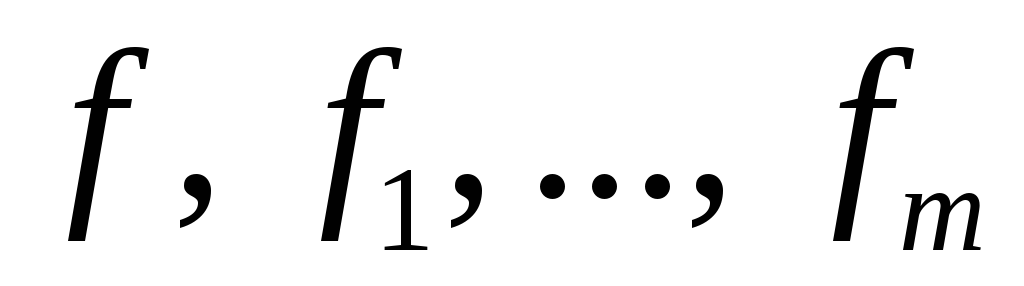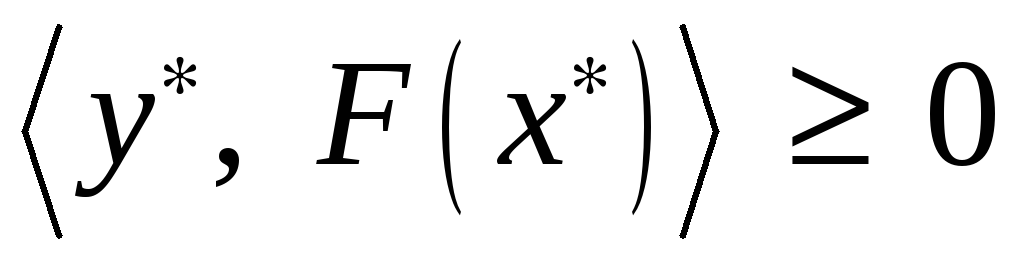§1. Общий подход к решению задач нелинейного программирования.
К задачам нелинейного программирования относятся такие задачи на условный экстремум, в которых нелинейны либо целевая функция , либо, по крайней мере, одна из функций, образующих область допустимых решений, либо нелинейны и целевая функция и функции-ограничения.
Задача нелинейного программирования (задача НП) в общем виде формулируется следующим образом :
где хотя бы одна из функций f, 1, 2. m нелинейна.
Предположим, что все эти функции дифференцируемы. Тогда для определения условного экстремума могут быть использованы методы дифференциального исчисления. Процесс решения будет состоять
1) в определении внутри допустимого множества всех стационарных точек функции f, удовлетворяющих условию =0; j=1,2,…, n;
2) определении той стационарной точки, которая доставляет наибольшее значение функции f внутри области;
3) нахождении максимума функции f внутри каждой границы области и выборе наибольшего ее значения по всем границам;
4) нахождении наибольшего значении функции f в вершинах области;
5) нахождении глобального максимума функции f.
Как видим, решение задачи НП значительно сложнее решения задачи линейного программирования. Для решения последней требовалось исследовать значение целевой функции лишь в вершинах области, да и то не во всех.
§2. Задачи выпуклого программирования
Определение I. Множество называется выпуклым, если отрезок, соединяющий любые две точки множества, также принадлежит этому множеству. Ниже приводятся графические примеры выпуклых (a) и невыпуклых (b) множеств. ( рис. 1)
сякая точка Р отрезка, соединяющего точки Р1, Р2, выражается через эти точки следующим образом:
Каждой точке отрезка соответствует определенное значение λ. Равенство называется выпуклой комбинацией точек Р1 и Р2. Поэтому можно дать другое определение выпуклого множества: множество называется выпуклым, если оно содержит любую выпуклую комбинацию любых двух точек Р1 и Р2, из этого множества.
Определение II. Функция f называется выпуклой на заданном выпуклом множестве, если выполняется следующее неравенство:
Ниже изображена выпуклая функция Z= f (x1, x2) (рис. 2).
ричем M1 = f (P1), M2 = f (P2), M = f (P). Согласно определению выпуклой функции можно записать
Неравенство означает, что все точки поверхности функции, соответствующие отрезку Р1, Р2, лежат не ниже отрезка М1М2. Если функция выпуклая, то такое свойство будет выполняться обязательно.
Определение III. Функция f называется вогнутой на заданном выпуклом множестве, если выполняется следующее неравенство:
На рис. 2 изображена вогнутая функция Z= f (x1, x2). Причем M1 = f (P1), M2 = f (P2),
= f (P). Согласно определению вогнутой функции можно записать
Неравенство означает, что все точки поверхности функции, соответствующие отрезку Р1Р2, лежат не выше отрезка М1М2. Для вогнутых функций такое условие выполняется всегда.
Выпуклые и вогнутые функции имеют большое значение в нелинейном программировании вследствие следующих очевидных свойств этих функций.
1.Сумма выпуклых (вогнутых) функций есть выпуклая (вогнутая) функция.
2.Локальный максимум строго выпуклой функции является ее глобальным максимумом и достигается в единственной точке выпуклого множества, в котором задана функция (рис. 3)
3. Локальный минимум строго вогнутой функции является ее глобальный минимум и достигается в единственной точке выпуклого множества, в котором задана функция (рис. 3)
4. Если выпуклая ( вогнутая) функция не имеет экстремума, то она достигает наименьшего и наибольшего значения на границе выпуклой области ( рис. 4)
5.Если функции i (x1, x2,…, xn); i=1,2,…,m — выпуклые (вогнутые), то множество, образуемое условиями
§3. Задача выпуклого программирования.

где Ф(Х) – выпуклая функция,D – выпуклое не пустое ограниченное и замкнутое множество. Напомним, что по определению выпуклая функция является непрерывной.
Как показано в предыдущем параграфе, во внутреннихточках множества допустимых значенийDфункцияФ(Х) достигает минимального значения в точках, которые являются ее либо стационарными, либо критическими точками. Однако функция может достигать своего наименьшего значения ив граничных точкахобласти определенияD.
Важные свойства задачи выпуклого программирования определяют две следующие теоремы.
Теорема 1. ЕсливнутренняяточкамножестваD является точкой локального минимума в задаче выпуклого программирования, то в этой точке функцияФ(Х) достигает свой глобальный минимум.
Доказательство.Положим, что в точке




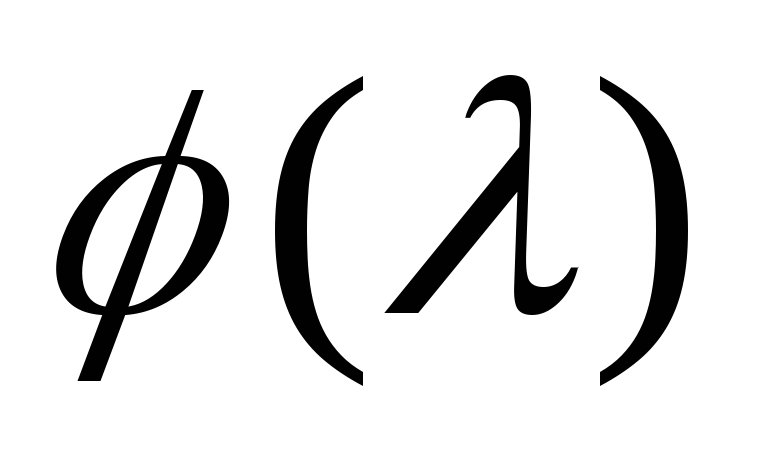


Это значит, что существует окрестность 




Из теоремы следует, что во всех точках локального минимума выпуклая функция имеете одинаковые значения.
Пример 1. Рассмотрим не строго выпуклую квадратичную функцию, определенную в области (рисунок 1). Все локальные минимумы этой функции равны нулю и расположены на прямой
.
Рисунок 1 — К примеру 1
Теорема 2. ФункцияФ(Х), строго выпуклая на выпуклом множестве, имеет в этом множестве одну точку минимума (глобального)●
Условия существования решения задачи выпуклого программирования дает следующая теорема.
Теорема 3. Пусть функцияФ(Х) выпукла на выпуклом множестве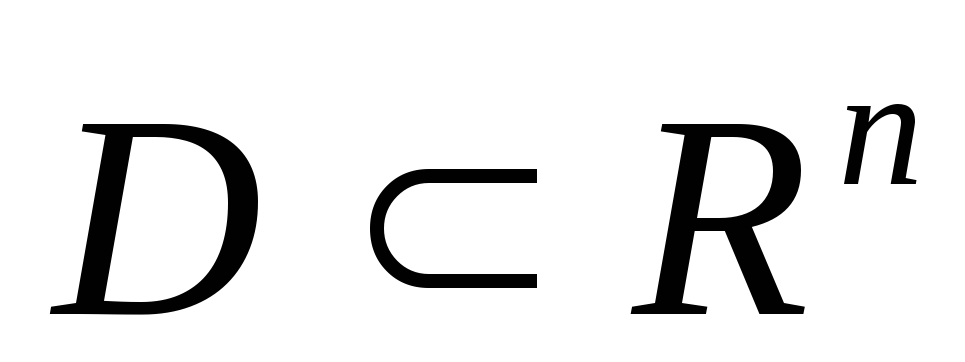


. (1)
Необходимость. Рассмотрим сечение




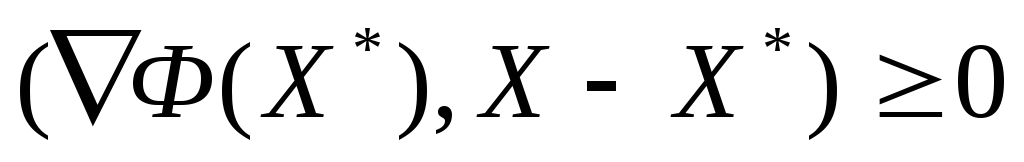
Достаточность. Пусть в точке







Теорему 3 иллюстрирует рисунок 2.
Рисунок 2 — К теореме 2
На рисунке 2 точка 

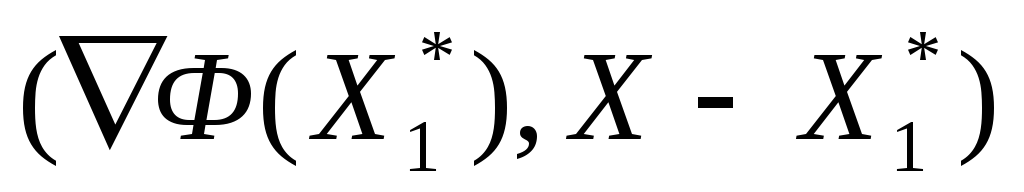



Линии уровня на рисунке 2 получены с помощью следующей MATLAB-программы:
Заметим, что если точка 


REVIZED / 11_Выпуклое_программирование!
Определение 1. Задачей выпуклого программирования называется задача нелинейного программирования, где все функции являются выпуклыми.
Таким образом, задача выпуклого программирования является задачей условной минимизации, где целевая функция выпукла и допустимая область представляет собой выпуклое множество, образованное системой выпуклых неравенств. Поэтому утверждения, полученные ранее в пара-графе 6, справедливы для задачи выпуклого программирования. В данном параграфе мы конкретизируем эти общие результаты и приведем их в форму более удобную для исследования и решения следующей задачи выпуклого программирования:
(1)
, (2)
. (3)
Нам понадобятся некоторые вспомогательные построения в пространстве 





Для задачи (1) – (3) определим множество
,
где .
Лемма. Для задачи выпуклого программирования (1) – (3) множество выпукло.
Доказательство. Выберем произвольные векторы 

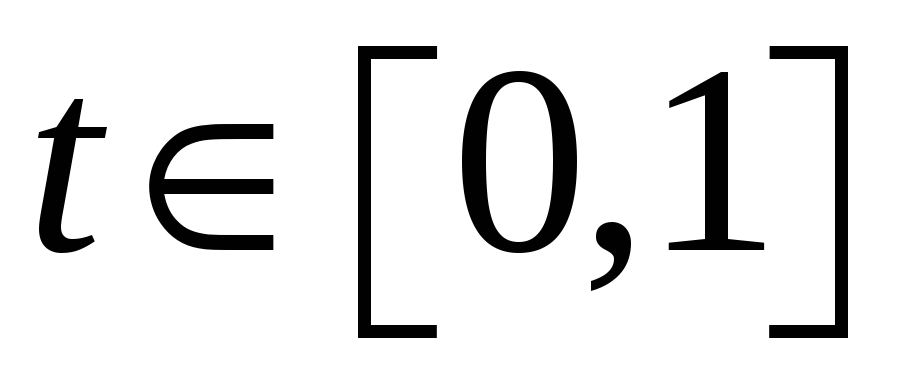







,
.
Из полученных неравенств и вытекает выпуклость множества .
Теорема 1. (Теорема Куна-Таккера в форме о седловой точке функции Лагранжа задачи выпуклого программирования) Пусть в задаче выпуклого программирования (1) – (3) система (2) удовлетворяет условию Слейтера относительно 

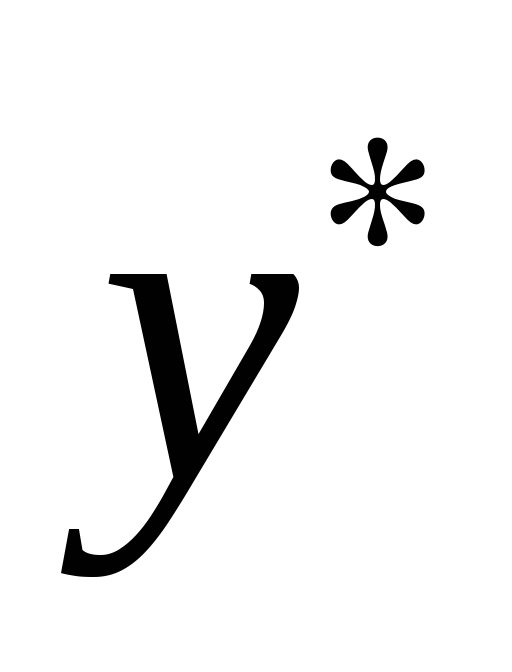

Доказательство. Поскольку достаточность этого условия уже доказана для произвольной задачи нелинейного программирования (см. теорему 2.6 введения), осталось доказать только необходимость.
Необходимость. Пусть 





Убедимся, что 

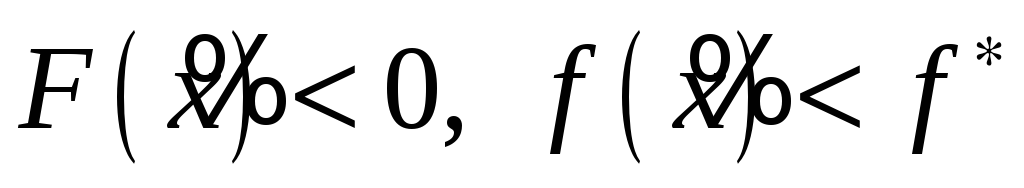


Итак, 

вектор 


. (4)
Убедимся далее, что все координаты вектора 





Легко увидеть, что при любом 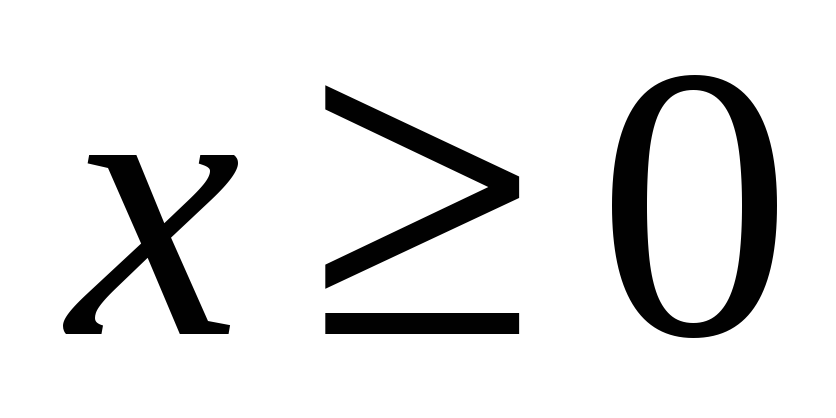


. (5)
Покажем, что 






Обозначим 


. (6)
Отсюда при следует
. (7)
С другой стороны, так как 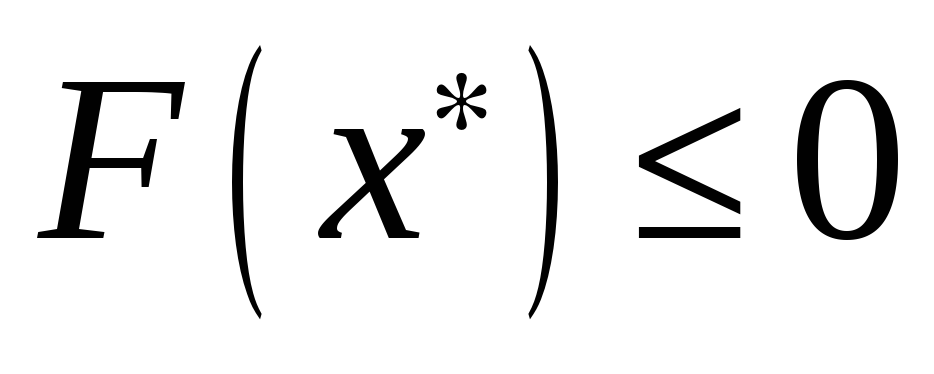

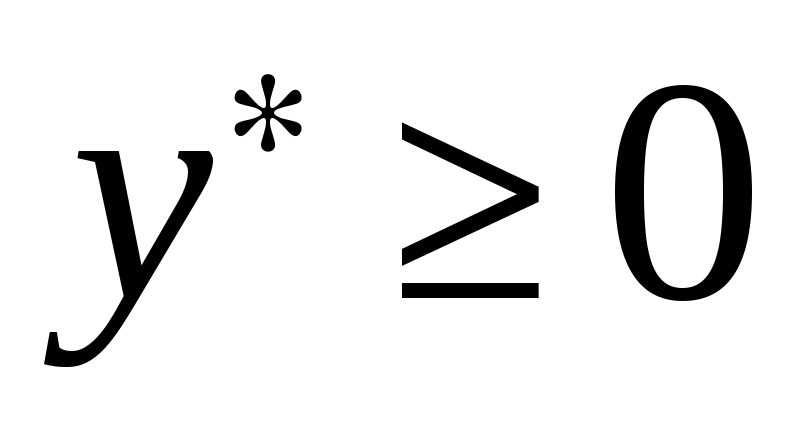
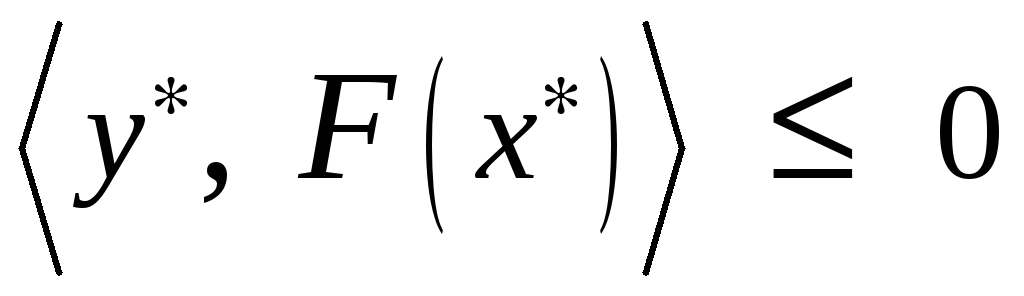

. (8)
,
(9)
Далее, пусть 

.
. (10)
Неравенства (9), (10) и означают, что – седловая точка функции Лагранжа задачи выпук-
лого программирования. Что и требовалось.
Прежде, чем познакомиться с еще одним вариантом теоремы Куна-Таккера, приведем следующую теорему, которая представляет собой критерий условного минимума в терминах конусов опорных векторов.
Теорема 2. Пусть 





. (11)
Доказательство следует непосредственно из теоремы 6.5 и определения конуса 


Теорема 3. (Теорема Куна-Таккера в дифференциальной форме для задачи выпуклого программирования) Пусть дана задача выпуклого программирования в виде (1), (2), где все функции 


, (12)
.
Доказательство. Покажем, что условия (12) и (13) эквивалентны включению (11). Пусть точка 


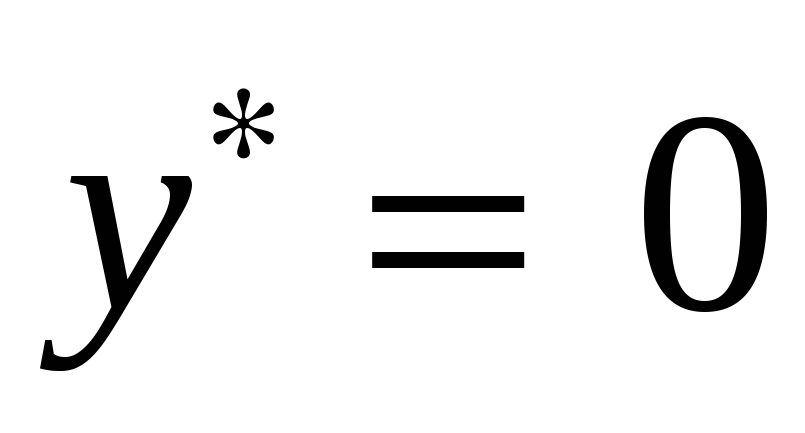
Пусть теперь 





В заключение параграфа приведем формулировки двух теорем Куна-Таккера для задачи вы-
пуклого программирования с линейными ограничениями.
Теорема 4. Пусть в задаче выпуклого программирования (1) – (3) система ограничений (2) имеет вид 



существовал неотрицательный вектор 

Отметим, что в этом случае функция Лагранжа имеет вид .
Теорема 5. Пусть в задаче выпуклого программирования (1), (2) целевая функция 
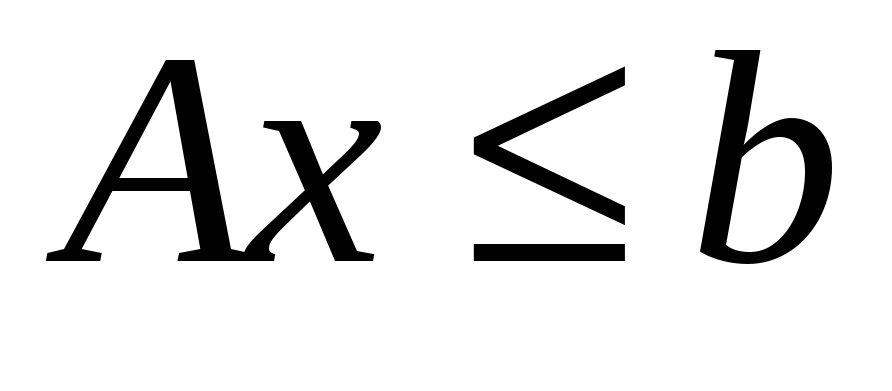





Заметим, что в теоремах 4 и 5 не требуется выполнения условия Слейтера, поэтому они не являются частными случаями теорем 1 и 3 и требуют самостоятельного доказательства.