Общая постановка задач динамического программирования.
Рассмотрим управляемый процесс. Например, распределение средств между предприятиями, использующими ресурсы в течение ряда лет.
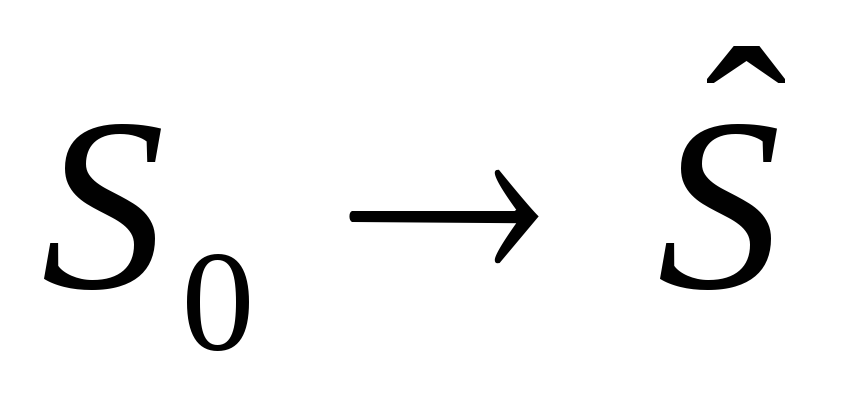
В результате управления система (объект) Sпереходит из состояния

Пусть управление можно разбить на nшагов, то есть решения принимаются последовательно на каждом шаге, а управление, переводящее системуSиз


Пусть 
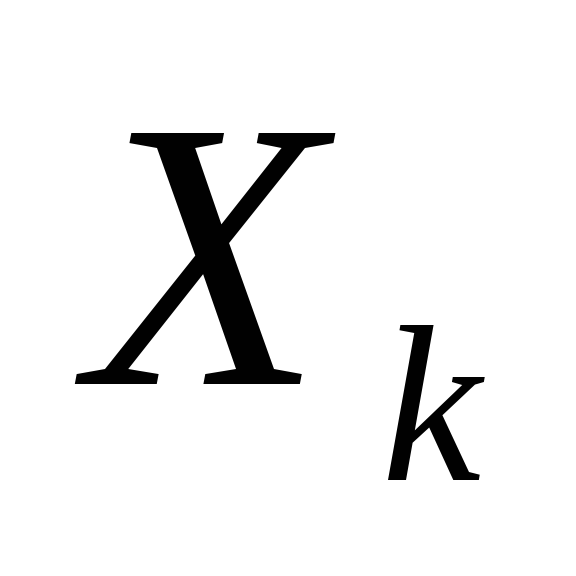
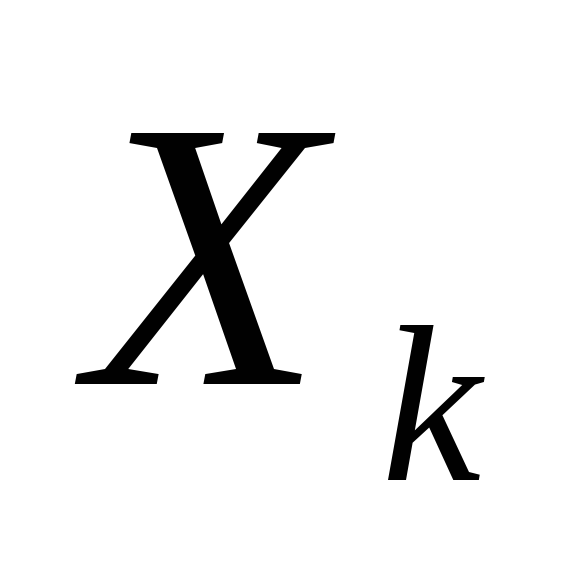




- Состояние
зависит только от предыдущего состояния
и управления на предыдущем шаге и не зависит от предшествующих состояний и управлений. Это требование называется «отсутствие последствий».
— уравнение состояний.
- Целевая функция является аддитивной от показателей эффективности на каждом шаге. Обозначим показатель эффективности к-ого шаге через:


- Задача оптимизации интерпретируется как n-шаговый процесс управления.
- Целевая функция равна сумме целевых функций на каждом шаге.
- Выбор управления на k-ом шаге зависит от состояния системы к этому шагу, не влияет на предшествующие шаги (отсутствие обратной связи).
- Состояние послеk-ого шага зависит только от предшествующего состояния
и управления
(нет последствий).
- На каждом шаге управление
зависит от конечного числа управляющих переменных, а состояние
от конечного числа параметров.
Вычислительная схема задач динамического программирования безразлична к способам задания функции и ограничений, связана с принципом оптимальности и использует рекуррентные соотношения.
Принцип оптимальности.
Принцип оптимальности(был предложен Беллманом в 1953 г.): каково бы ни было состояние системыSв результате какого либо числа шагов, на ближайшем шаге надо выбирать управление так, чтобы оно в совокупности с оптимальными управлениями на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный. Основное требование принципа оптимальности состоит в том, что процесс управления должен быть без обратных связей, то есть управление на каждом шаге не должно оказывать влияние на предшествующие шаги. При оптимальном управлении, утверждается, что любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого процесса по отношению к исходному состоянию этого процесса. Следовательно, решение на каждом шаге является наилучшим с точки зрения управления в целом.
1.nbsp; nbsp; Вычислительная схема метода динамического программирования:
a)nbsp; nbsp; зависит от
1.nbsp; nbsp; Вычислительная схема способа динамического программирования:
a)nbsp; nbsp; зависит от способов задания функций;
b)nbsp; nbsp; зависит от методов задания ограничений;
c)nbsp; nbsp; связана с принципом оптимальности Беллмана. (*ответ к тесту*)
2.nbsp; nbsp; Какую задачку можно решить методом динамического программирования:
a)nbsp; nbsp; транспортную задачку;
b)nbsp; nbsp; задачку о замене оборудования; (*ответ к тесту*)
c)nbsp; nbsp; принятия решения в конфликтной ситуации.
3.nbsp; nbsp; Способ наибыстрейшего спуска является:
a)nbsp; nbsp; способом множителей Лагранжа;
b)nbsp; nbsp; градиентным способом; (*ответ к тесту*)
c)nbsp; nbsp; методом кусочно-линейной аппроксимации.
4.nbsp; nbsp; nbsp;nbsp;Множители Лагранжа в экономическом смысле описывают:
a)nbsp; nbsp; доход, соответствующий плану;
b)nbsp; nbsp; издержки ресурсов;
c)nbsp; nbsp; стоимость (оценку) ресурсов. (*ответ к тесту*)
5.nbsp; nbsp; nbsp;nbsp;Функция нескольких переменных называется сепарабельной, если она может быть представлена в виде:
a)nbsp; nbsp; суммы функций одной переменной; (*ответ к тесту*)
b)nbsp; nbsp; творения функций нескольких переменных;
c)nbsp; nbsp; суммы выпуклых функций.
6.nbsp; nbsp; nbsp;nbsp;Платежной матрицей именуется матрица, элементами которой являются:
a)nbsp; nbsp; годовые прибыли отраслевых компаний;
b)nbsp; nbsp; выигрыши, соответствующие стратегиям игроков; (*ответ к тесту*)
c)nbsp; nbsp; налоговые платежи предприятий.
7.nbsp; nbsp; nbsp;nbsp;Верхней ценой парной забавы является:
a)nbsp; nbsp; гарантированный выигрыш игрока А при любой стратегии игрока В;
b)nbsp; nbsp; гарантированный выигрыш игрока В;
c)nbsp; nbsp; гарантированный проигрыш игрока В. (*ответ к тесту*)
8.nbsp; nbsp; nbsp;nbsp;Незапятанной ценой забавы именуется:
a)nbsp; nbsp; верхняя стоимость игры;
b)nbsp; nbsp; нижняя стоимость забавы;
c)nbsp; nbsp; общее значение верхней и нижней ценой забавы. (*ответ к тесту*)
9.nbsp; nbsp; nbsp;nbsp;Вероятно ли привести матричную забаву к задачке линейного программирования:
a)nbsp; nbsp; возможно; (*ответ к тесту*)
b)nbsp; nbsp; невероятно;
c)nbsp; nbsp; вероятно, если платежная матрица единичная.
Метод динамического программирования
Метод динамического программирования основан на пошаговой оптимизации целевой функции, где в качестве такой функции могут выступать стоимость, ресурсные затраты, финансово-экономические затраты, а также кратчайшие пути. Рассмотрим пример топологической оптимизации.
Пример 1. Пусть дана карта местности (рис. 10.3). Разбиваем эту карту координатной сеткой. Шаг сетки выбираем, исходя из условия точности. Узлы координатной сетки считаем вершинами графа.
Рис. 10.3. Карта местности
Проставляем веса ребер, учитывая, какая цель преследуется. Построение пути осуществляем из конечной вершины в начальную, исходя из следующих приоритетных направлений: вниз и вправо (при движении к конечной вершине). На первом этапе движения до конечной вершины В вынужденные, т.е. вниз и вправо (рис. 10.4, а). На последующих шагах направление движения определяется оптимизацией длин путей (рис. 10.4, б).
Рис. 10.4. Выбор кратчайшего пути: а — первый шаг; б — второй шаг; в — траектория пути
В результате выполнения операций определяется длина пути между вершинами (22 единицы) и траектория движения (по стрелкам), показанная на рис. 10.4, в.
Метод динамического программирования рассматривает многостадийные процессы принятия решения. При постановке задачи динамического программирования формируется некоторый критерий. Процесс разбивается на стадии (шаги), в которых принимаются решения, приводящие к достижению общей поставленной цели. Таким образом, метод динамического программирования — это метод пошаговой оптимизации.
Введем функцию fr определяющую минимальную длину пути из начальной вершины в вершину /. Обозначим через S- длину пути между вершинами inj,afj— наименьшую длину пути между вершиной j и начальной вершиной. Выбирая в качестве i такую вершину, которая минимизирует сумму (S- + fj), получаем уравнение
Трудность решения этого уравнения состоит в том, что неизвестная функция входит в обе части равенства. В такой ситуации приходится прибегать к классическому методу последовательных приближений (итераций), используя рекуррентную формулу
гдtfj k) — k-e приближение функции.
Возможен другой подход к решению поставленной задачи с помощью метода стратегий. При движении из начальной точки i в конечную точку к получается приближение = Sik, где Sik — длина пути между точками i и к.
Следующее приближение — поиск решения в классе двузвенных ломаных. Дальнейшие приближения отыскивают в классе трехзвенных, четырехзвенных и других ломаных.
Пример 2. Используя метод динамического программирования, найти кратчайший путь между вершинами 1 и 6 в графе на рис. 10.5.
Первый этап алгоритма — поиск длины минимального пути. Для вершины 1 имеем/j = 0, так как для этой вершины никакой путь еще не пройден.
Имеем^ = minfiS’jj + /j> =2 + 0 = 2 ;/3 = тш13 +/J = 4 + 0 = 4; Из рис. 10.5 видно, что из вершины 1 в вершину 4 возможны два пути (1—4) и (1—2—4), поэтому функция 7^ будет иметь вид
откуда выбирается минимальное значение функции/^ = 5. Аналогичным способом определяются значения функций/5 и/6:
Рис. 10.5. Исходный граф (а) и соответствующая ему матрица смежности (б)
Из последних соотношений находим, что имеют место следующие минимальные значения:/5 = 5,/6 = 7. Таким образом, в результате выполнения первого этапа алгоритма найдено, что кратчайший путь из вершины 1 в вершину 6 равен 7.
На втором этапе алгоритма будет найдена последовательность вершин, через которые проходит вычисленный минимальный путь. Для этого необходимо найти последовательность тех функций, которым соответствовал выбираемый минимум. Для функции/6 минимум вычислялся через значение функцииВ свою очередь, минимум функции/5 был вычислен через минимальное значение функции /2, а оно, в свою очередь, — через минимальное значение функции/г Следовательно, «отработка назад» от конечной вершины 6 искомого пути до его начальной вершины 1 позволяет указать последовательность проходимых при этом вершин графа: (1—2—5—6).
Пример 3. Определить кратчайший путь из вершины 1 в вершину 10 для графа, представленного на рис. 10.6.
Рис. 10.6. Взвешенный ориентированный граф
Находим последовательно значения функции/^, (в условных единицах) для каждой вершины ориентированного графа:
Длина кратчайшего пути составляет 14 условных единиц. Для выбора оптимальной траектории движения следует выполнить просмотр функций/^.в обратном порядке, т.е. с/,0 Пусть ft = /|0. В данном случае
Получаем, что (3 + /8) = 14, т.е./=/8. Значит, из вершины 10 следует перейти к вершине 8. Имеем])=/%• Рассмотрим функцию
Таким образом, получаем кратчайший путь от вершины 1 к вершине 10:
Рассмотренный метод определения кратчайшего пути может быть распространен и на неориентированные графы.
Пример 4. Для графа (рис. 10.6) найти кратчайший путь от вершины 1 до вершины 10, рассматривая граф как неориентированный. Матрица смежности весов графа в этом случае имеет вид:
Записываем выражения для функции^.:

Указанные целевые функции представляют собой систему линейных алгебраических уравнений (в примере 10 уравнений и 10 неизвестных).
Рассмотрим один из вариантов ее решения, учитывая, что/, = 0. Тогда имеем:
Подставив выражение для./^ в/5, получим Тогда
Окончательно имеем:/, = 17;/10 = 14.
Таким образом, кратчайший путь равен (1-4-6—8—10).

 зависит только от предыдущего состояния
зависит только от предыдущего состояния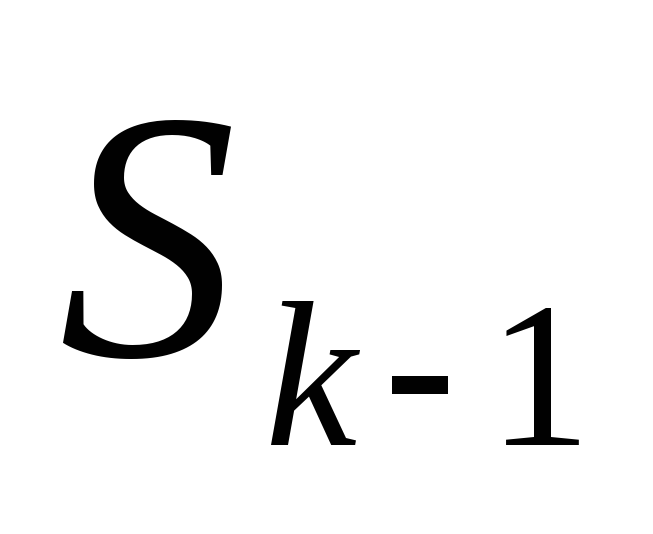 и управления на предыдущем шаге и не зависит от предшествующих состояний и управлений. Это требование называется «отсутствие последствий».
и управления на предыдущем шаге и не зависит от предшествующих состояний и управлений. Это требование называется «отсутствие последствий». — уравнение состояний.
— уравнение состояний. и управления
и управления (нет последствий).
(нет последствий). зависит от конечного числа управляющих переменных, а состояние
зависит от конечного числа управляющих переменных, а состояние от конечного числа параметров.
от конечного числа параметров.















