- Транспонирование и умножение матриц на Python
- Транспонирование матрицы
- Программа Python для транспонирования матрицы
- Умножение матриц
- Умножение двух матриц
- Способ 1: Использование метода вложенного цикла
- Способ 2: Использование метода понимания вложенного списка
- Transpose of a Matrix in Python
- Introduction to Matrix Transpose in Python
- Transpose of a Matrix using Nested Loop
- Transpose of a Matrix using Nested List Comprehension
- Transpose of a Matrix using Zip
- Transpose of a Matrix using NumPy Library
- For Square Matrix
- For Rectangular Matrix
- Conclusion
- Learn More:
- Линейная алгебра на Python. [Урок 2]. Транспонирование Матрицы
- Транспонирование матрицы
- P.S.
Транспонирование и умножение матриц на Python
В этом уроке мы напишем программы на Python для транспонирования и умножения матриц и вывода результатов.
Прежде чем писать программу транспонирования матрицы на Python, давайте сначала посмотрим на обзор транспонирования.
Транспонирование матрицы
Если вы заменяете строки матрицы столбцом той же матрицы, это называется транспонированием матрицы. Обозначается как X’. Например: Элемент в i-й строке и j-м столбце в X будет помещен в j-ю строку и i-й столбец в X’.
Пример: Предположим, мы взяли следующую матрицу A:
A = [[5, 4, 3] [2, 4, 6] [4, 7, 9] [8, 1, 3]]
At будет транспонированием указанной выше матрицы, т. е. A [i] [j] = At [j] [i], и поэтому At должно быть:
В = [5, 2, 4, 8] [4, 4, 7, 1] [3, 6, 9, 3]
Программа Python для транспонирования матрицы
Теперь мы напишем программу на Python для транспонирования входной заданной матрицы, где мы выполняем операцию, как мы выполнили в приведенном выше примере. Чтобы выполнить операцию транспонирования матрицы, мы будем использовать метод вложенного цикла for.
Давайте разберемся с использованием и реализацией этого метода на следующем примере.
# Define a matrix A A = [[5, 4, 3], [2, 4, 6], [4, 7, 9], [8, 1, 3]] # Define an empty matrix of reverse order transResult = [[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]] # Use nested for loop on matrix A for a in range(len(A)): for b in range(len(A[0])): transResult[b][a] = A[a][b] # store transpose result on empty matrix # Printing result in the output print("The transpose of matrix A is: ") for res in transResult: print(res) The transpose of matrix A is: [5, 2, 4, 8] [4, 4, 7, 1] [3, 6, 9, 3]
Умножение матриц
В этом разделе мы напишем программу на Python для умножения двух входных матриц и выведем результат на выходе. Эта программа укажет, как умножать две матрицы, имеющие определенные значения.
Прежде чем писать программу на Python, давайте сначала посмотрим на обзор умножения двух матриц.
Умножение матриц — это бинарная операция, в которой используется пара матриц для создания другой матрицы. Элементы в матрице умножаются в соответствии с элементарной арифметикой.
При умножении двух матриц элементы строки первой матрицы умножаются на элементы столбца второй матрицы.
Пример: предположим, что мы взяли следующие две матрицы A и B:
A = [[5, 4, 3] [2, 4, 6] [4, 7, 9]] and, B = [[3, 2, 4] [4, 3, 6] [2, 7, 5]]
C будет объединением двух указанных выше матриц, т. е. C = A + B, и поэтому C должно быть:
C = [[37, 43, 59] [34, 58, 62] [58, 92, 103]]
Как мы видим, результирующая матрица C, также известная как произведение матриц, имеет то же количество строк, что и первая матрица (матрица A), и такое же количество столбцов, как и вторая матрица (матрица B). Мы также знаем этот тип умножения матриц как скалярное произведение матриц.
Умножение двух матриц
Теперь мы напишем программу Python для умножения двух матриц, где мы выполняем умножение, как мы это делали в приведенном выше примере. Мы можем использовать различные методы для написания такой программы на Python, но в этом руководстве будем использовать только следующие два метода:
- Использование метода вложенного цикла.
- Использование метода понимания вложенного списка.
В обоих методах мы напишем пример программы, чтобы понять их реализацию для умножения двух матриц.
Способ 1: Использование метода вложенного цикла
В этом методе мы собираемся использовать вложенный цикл for для двух матриц, выполнять над ними умножение и сохранять результат умножения в третьей матрице в качестве итогового значения.
Давайте разберемся с реализацией этого метода на следующем примере.
# Define two matrix A and B in program A = [[5, 4, 3], [2, 4, 6], [4, 7, 9]] B = [[3, 2, 4], [4, 3, 6], [2, 7, 5]] # Define an empty matrix to store multiplication result multiResult = [[0, 0, 0], [0, 0, 0], [0, 0, 0]] # Using nested for loop method on A & B matrix for m in range(len(A)): for n in range(len(B[0])): for o in range(len(B)): multiResult[m][n] += A[m][o] * B[o][n] # Storing multiplication result in empty matrix # Printing multiplication result in the output print("The multiplication result of matrix A and B is: ") for res in multiResult: print(res) The multiplication result of matrix A and B is: [37, 43, 59] [34, 58, 62] [58, 92, 103]
Способ 2: Использование метода понимания вложенного списка
В этом методе мы будем использовать понимание вложенного списка, чтобы получить результат умножения двух входных матриц. При использовании в программе метода понимания списка мы также будем использовать «zip в Python» для вложенного списка. Давайте разберемся с реализацией этого метода на следующем примере.
# Define two matrix A & B in the program A = [[5, 4, 3], [2, 4, 6], [4, 7, 9]] B = [[3, 2, 4], [4, 3, 6], [2, 7, 5]] # Using nested list method with zip in Python multiResult = [[sum(a * b for a, b in zip(Arow, Bcol)) for Bcol in zip(*B)] for Arow in A] # Printing multiplication result in the output print("The multiplication result of matrix A and B is: ") for res in multiResult: print(res) The multiplication result of matrix A and B is: [37, 43, 59] [34, 58, 62] [58, 92, 103]
Transpose of a Matrix in Python
The transpose of a matrix is nothing but a matrix obtained by changing the rows into columns and columns into rows. If a matrix is initially N x M , then after the transpose, the matrix becomes M x N . We can denote the transpose of a matrix (A) by A’ or A^T. Transpose of a matrix in python can be implemented in various ways such as nested loops, nested list comprehension, zip() function, and transpose() function of NumPy library.
Introduction to Matrix Transpose in Python
Before learning how to transpose a matrix in Python, we should first understand the matrix and transpose of a matrix.
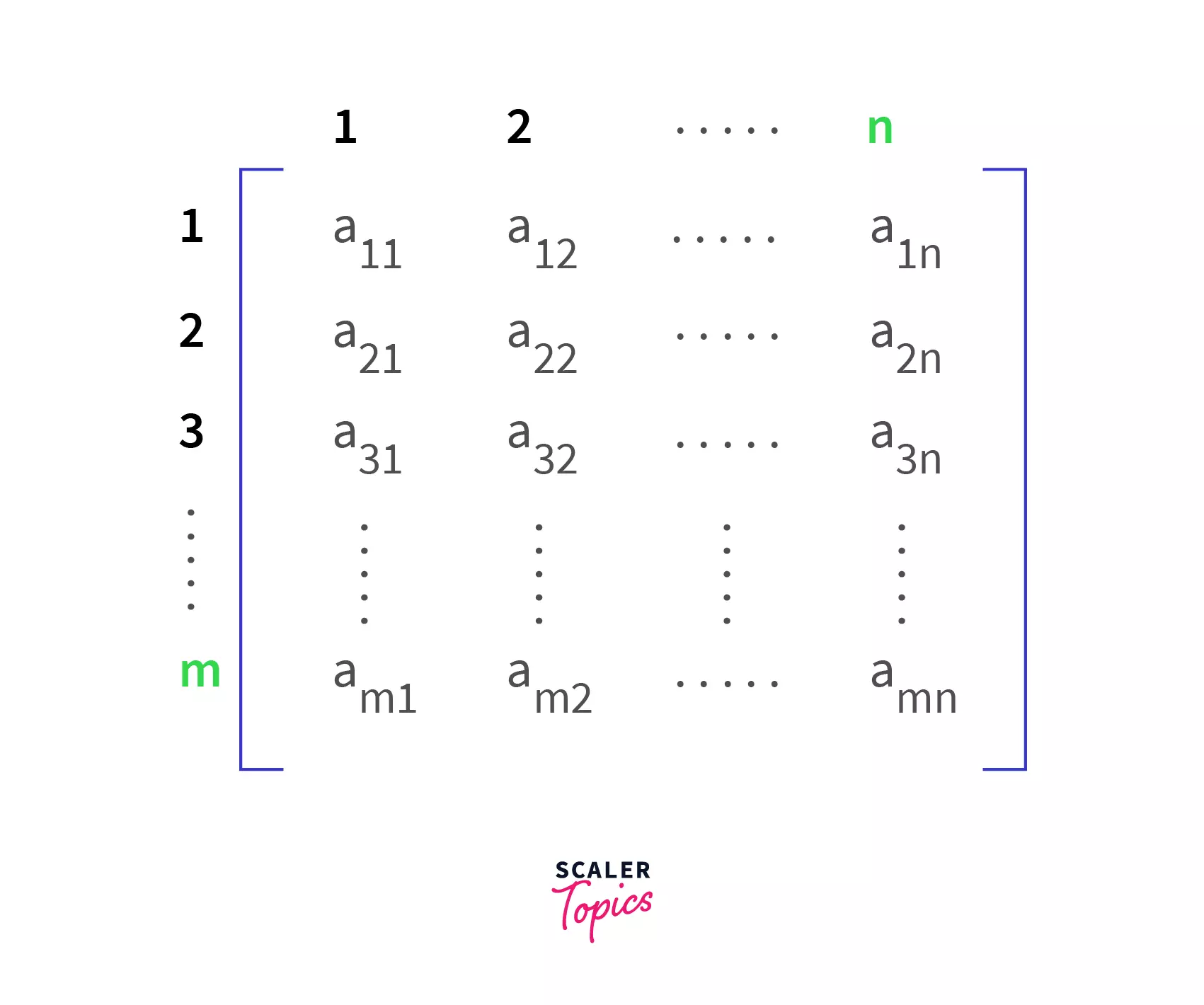
A matrix is a rectangular array of some data(numbers, letters, or other objects) arranged in the form of rows and columns. A matrix is composed of rows and columns. If the number of rows is N and the number of columns is M. Then we say the matrix is a N x M matrix. Refer to the image below to see how a matrix is represented using subscripts.
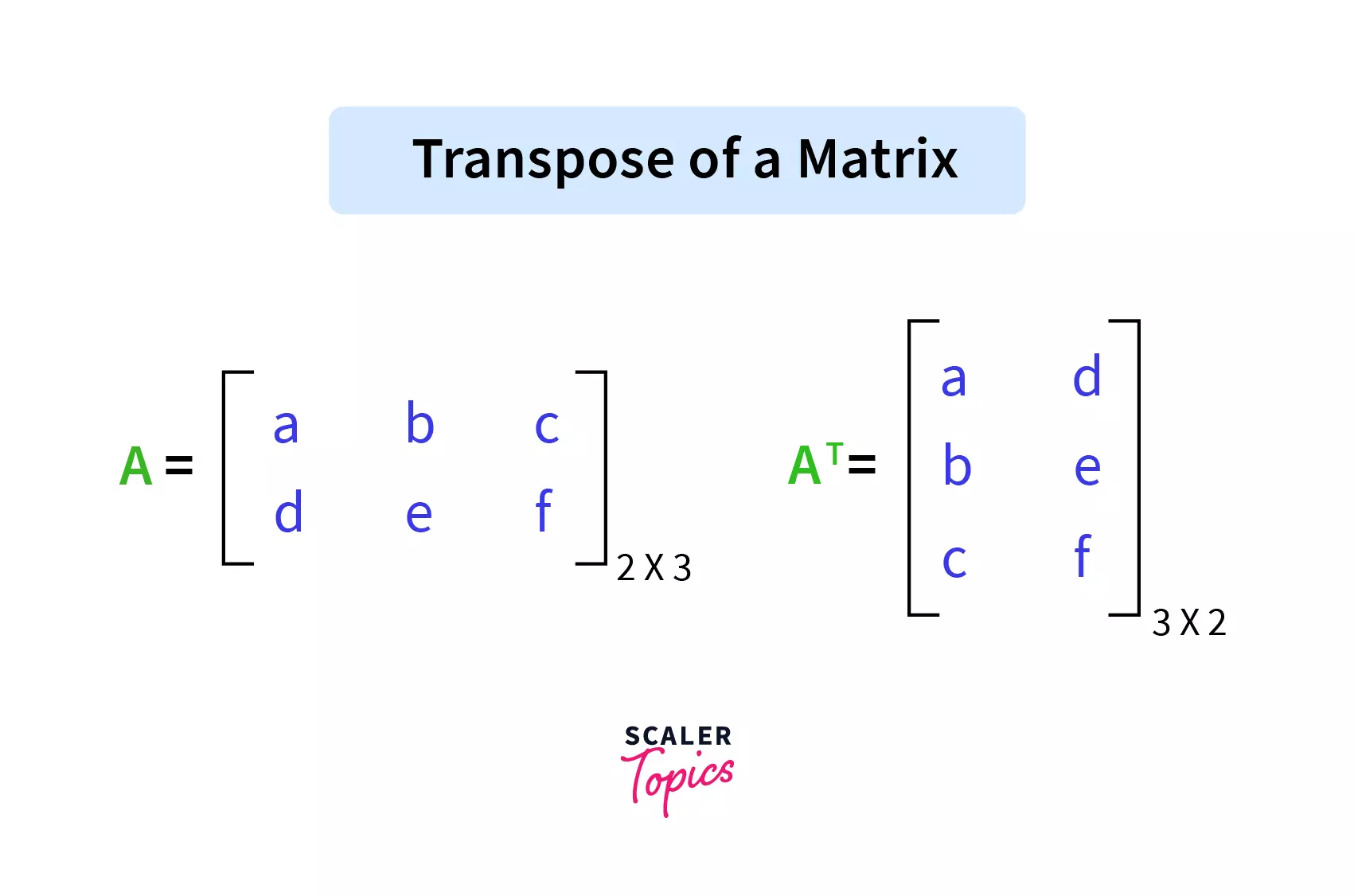
Now, the transpose of the matrix is nothing but a matrix obtained by changing the rows into columns and columns into rows. If a matrix is initially N x M (N is several rows and M is several columns), then after the transpose, the matrix becomes M x N (M is the number of rows and N is several columns). Refer to the image below to visualize the transpose of a matrix.
Note: Transpose of a matrix A is denoted by either A’ or A^T.
Now, in python a matrix can be implemented using nested lists. Example: matrix = [[1, 2], [2, 3], [3, 4]] As we can see, the matrix has 3 rows and 2 columns so it is a 3×2 matrix. We can visualize the matrix as:
After the transpose, the matrix has 2 rows and 3 columns so it becomes a 2×3 matrix. The transpose of the matrix will look like as shown below:
The transpose of a matrix in Python can be implemented in various ways. Let us now discuss them one by one.
Transpose of a Matrix using Nested Loop
As we have seen, we can implement a matrix using nested lists(lists inside a list). So, we can use a nested loop (loop inside another loop). By running two loops (using I and j variables), we can change the value present at the ith row and jth column to the jth row and ith column. Refer to the code below for a better understanding.
Here, we are placing the matrix[i][j] element into the transpose[j][i] .
Transpose of a Matrix using Nested List Comprehension
We have seen how to get transpose of a matrix in python using nested loops, but we can also use the pythonic way (shorter way). List comprehension (creating lists based on existing iterables) is very frequently used in these scenarios as list comprehension helps us to write concise codes (codes which take less space). Refer to the code below for a better understanding.
Transpose of a Matrix using Zip
We can also obtain the transpose of a matrix in python using the map() function and zip() function.
- map() is a function that works as an iterator, it returns a result after applying the provided function on each of its iterable items.
- zip(iterable) is also a function that takes iterables as arguments and returns an iterator.
Let us see the code for better understanding.
Transpose of a Matrix using NumPy Library
So far, we have seen all the built-in methods of getting the transpose of a matrix in python. We can use a library named NumPy , built to work around arrays. The NumPy library helps us to work with large data sets and supports various methods that help us to work with multi-dimensional arrays efficiently. We will use the transpose() function of the NumPy library. Let us see the code for a better understanding.
Note: Since NumPy is an external library, we need to install NumPy with the command `pip install NumPy.
For Square Matrix
The transpose of a square matrix results in another square matrix because the number of rows and columns are the same. Let us take an example of a square matrix ( NxN ):
For Rectangular Matrix
As we know, the transpose of an NxM matrix will result in an NxM matrix. Since N and M are of different values, the matrix is not considered a rectangular matrix. Let us take an example of the 2×5 matrix:
Conclusion
- A matrix is a rectangular array of some data(numbers, letters, or other objects) arranged in the form of rows and columns.
- The transpose of a matrix is nothing but a matrix obtained by changing the rows into columns and columns into rows. Transpose of a matrix A is denoted by either A’ or A^T.
- If a matrix is initially N x M , then after the transpose, the matrix becomes M x N .
- Transpose of a matrix in python can be implemented using nested loops, nested list comprehension, zip() function, and transpose() function of the NumPy library.
Learn More:
Линейная алгебра на Python. [Урок 2]. Транспонирование Матрицы
В этом уроке мы рассмотрим операцию “транспонирование матрицы” и как она выполняется на Python. Также разберем на примерах свойства этой операции.
Транспонирование матрицы
Транспонирование матрицы – это процесс замены строк матрицы на ее столбцы, а столбцов соответственно на строки. Полученная в результате матрица называется транспонированной. Символ операции транспонирования – буква T .
Транспонированная будет выглядеть так:
Решим задачу транспонирования матрицы на Python . Создадим матрицу A:
>>> A = np.matrix('1 2 3; 4 5 6') >>> print(A) [[1 2 3] [4 5 6]] Транспонируем матрицу с помощью метода transpose():
>>> A_t = A.transpose() >>> print(A_t) [[1 4] [2 5] [3 6]]
Существует сокращенный вариант получения транспонированной матрицы, он очень удобен в практическом применении:
Рассмотрим на примерах свойства транспонированных матриц. Операции сложения и умножение матриц, а также расчет определителя более подробно будут рассмотрены в последующих уроках.
Свойство 1 . Дважды транспонированная матрица равна исходной матрице:
>>> A = np.matrix('1 2 3; 4 5 6') >>> print(A) [[1 2 3] [4 5 6]] >>> R = (A.T).T >>> print(R) [[1 2 3] [4 5 6]] Свойство 2 . Транспонирование суммы матриц равно сумме транспонированных матриц:
>>> A = np.matrix('1 2 3; 4 5 6') >>> B = np.matrix('7 8 9; 0 7 5') >>> L = (A + B).T >>> R = A.T + B.T >>> print(L) [[ 8 4] [10 12] [12 11]] >>> print(R) [[ 8 4] [10 12] [12 11]] Свойство 3 . Транспонирование произведения матриц равно произведению транспонированных матриц расставленных в обратном порядке:
>>> A = np.matrix('1 2; 3 4') >>> B = np.matrix('5 6; 7 8') >>> L = (A.dot(B)).T >>> R = (B.T).dot(A.T) >>> print(L) [[19 43] [22 50]] >>> print(R) [[19 43] [22 50]] В данном примере, для умножения матриц, использовалась функция dot() из библиотеки Numpy.
Свойство 4 . Транспонирование произведения матрицы на число равно произведению этого числа на транспонированную матрицу:
>>> A = np.matrix('1 2 3; 4 5 6') >>> k = 3 >>> L = (k * A).T >>> R = k * (A.T) >>> print(L) [[ 3 12] [ 6 15] [ 9 18]] >>> print(R) [[ 3 12] [ 6 15] [ 9 18]] Свойство 5 . Определители исходной и транспонированной матрицы совпадают:
>>> A = np.matrix('1 2; 3 4') >>> A_det = np.linalg.det(A) >>> A_T_det = np.linalg.det(A.T) >>> print(format(A_det, '.9g')) -2 >>> print(format(A_T_det, '.9g')) -2 Ввиду особенностей Python при работе с числами с плавающей точкой, в данном примере вычисления определителя рассматриваются только первые девять значащих цифр после запятой (за это отвечает параметр ‘.9g’ ).
P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта . Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.