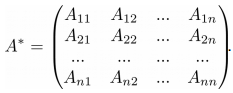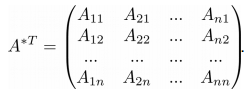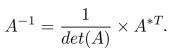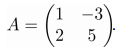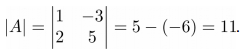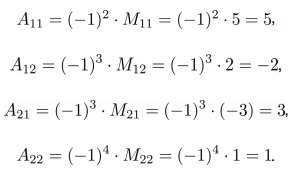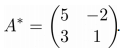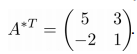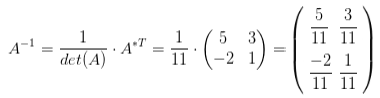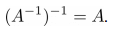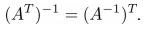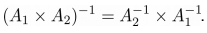Вычисление обратной матрицы python

Линейная алгебра на Python. [Урок 5]. Обратная матрица и ранг матрицы

Обратной матрицей A -1 матрицы A называют матрицу, удовлетворяющую следующему равенству:

где – E это единичная матрица.

Для того, чтобы у квадратной матрицы A была обратная матрица необходимо и достаточно чтобы определитель |A| был не равен нулю. Введем понятие союзной матрицы . Союзная матрица A* строится на базе исходной A путем замены всех элементов матрицы A на их алгебраические дополнения.

Транспонируя матрицу A*, мы получим так называемую присоединенную матрицу A* T :

Теперь, зная как вычислять определитель и присоединенную матрицу, мы можем определить матрицу A -1 , обратную матрице A:

Пример вычисления обратной матрицы. Пусть дана исходная матрица A, следующего вида:

Для начала найдем определитель матрицы A:

Как видно из приведенных вычислений, определитель матрицы не равен нулю, значит у матрицы A есть обратная. Построим присоединенную матрицу, для этого вычислим алгебраические дополнения для каждого элемента матрицы A:

Союзная матрица будет иметь следующий вид:

Присоединенная матрица получается из союзной путем транспонирования:

Решим задачу определения обратной матрицы на Python. Для получения обратной матрицы будем использовать функцию inv():

>>> A = np.matrix('1 -3; 2 5') >>> A_inv = np.linalg.inv(A) >>> print(A_inv) [[ 0.45454545 0.27272727] [-0.18181818 0.09090909]]

Рассмотрим свойства обратной матрицы.

Свойство 1 . Обратная матрица обратной матрицы есть исходная матрица:

>>> A = np.matrix('1. -3.; 2. 5.') >>> A_inv = np.linalg.inv(A) >>> A_inv_inv = np.linalg.inv(A_inv) >>> print(A) [[1. -3.] [2. 5.]] >>> print(A_inv_inv) [[1. -3.] [2. 5.]]

Свойство 2 . Обратная матрица транспонированной матрицы равна транспонированной матрице от обратной матрицы:

>>> A = np.matrix('1. -3.; 2. 5.') >>> L = np.linalg.inv(A.T) >>> R = (np.linalg.inv(A)).T >>> print(L) [[ 0.45454545 -0.18181818] [ 0.27272727 0.09090909]] >>> print(R) [[ 0.45454545 -0.18181818] [ 0.27272727 0.09090909]]

Свойство 3 . Обратная матрица произведения матриц равна произведению обратных матриц:

>>> A = np.matrix('1. -3.; 2. 5.') >>> B = np.matrix('7. 6.; 1. 8.') >>> L = np.linalg.inv(A.dot(B)) >>> R = np.linalg.inv(B).dot(np.linalg.inv(A)) >>> print(L) [[ 0.09454545 0.03272727] [-0.03454545 0.00727273]] >>> print(R) [[ 0.09454545 0.03272727] [-0.03454545 0.00727273]]

Ранг матрицы

Ранг матрицы является еще одной важной численной характеристикой. Рангом называют максимальное число линейно независимых строк (столбцов) матрицы. Линейная независимость означает, что строки (столбцы) не могут быть линейно выражены через другие строки (столбцы). Ранг матрицы можно найти через ее миноры, он равен наибольшему порядку минора, который не равен нулю. Существование ранга у матрицы не зависит от того квадратная она или нет.

Вычислим ранг матрицы с помощью Python. Создадим единичную матрицу:

>>> m_eye = np.eye(4) >>> print(m_eye) [[1. 0. 0. 0.] [0. 1. 0. 0.] [0. 0. 1. 0.] [0. 0. 0. 1.]]

Ранг такой матрицы равен количеству ее столбцов (или строк), в нашем случае ранг будет равен четырем, для его вычисления на Python воспользуемся функцией matrix_rank():

>>> rank = np.linalg.matrix_rank(m_eye) >>> print(rank) 4

Если мы приравняем элемент в нижнем правом углу к нулю, то ранг станет равен трем:

>>> m_eye[3][3] = 0 >>> print(m_eye) [[1. 0. 0. 0.] [0. 1. 0. 0.] [0. 0. 1. 0.] [0. 0. 0. 0.]] >>> rank = np.linalg.matrix_rank(m_eye) >>> print(rank) 3

P.S.

Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта . Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.

Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.

Линейная алгебра на Python. [Урок 5]. Обратная матрица и ранг матрицы : 1 комментарий

1. pedro kekulé 23.10.2019 i want that help me
   1) написать программу вычисляющую обратную матрицу 2) написать программу для решения СЛАУ с помощью обратной матрицы 3) сравнить скорость работы всех трёх методов решения СЛАУ

Источник

Inverse of a matrix using numpy

To calculate inverse of a matrix in numpy, say matrix M, it should be simply: print M.I Here’s the code:

x = numpy.empty((3,3), dtype=int) for comb in combinations_with_replacement(range(10), 9): x.flat[:] = comb print x.I 

I’m presuming, this error occurs because x is now flat, thus ‘ I ‘ command is not compatible. Is there a work around for this? My goal is to print the INVERSE MATRIX of every possible numerical matrix combination.

commented on the other answer also, but you have to defined x as a matrix np.matrix(x) so that the .I method is available.

5 Answers 5

The I attribute only exists on matrix objects, not ndarray s. You can use numpy.linalg.inv to invert arrays:

Note that the way you’re generating matrices, not all of them will be invertible. You will either need to change the way you’re generating matrices, or skip the ones that aren’t invertible.

try: inverse = numpy.linalg.inv(x) except numpy.linalg.LinAlgError: # Not invertible. Skip this one. pass else: # continue with what you were doing 

Also, if you want to go through all 3×3 matrices with elements drawn from [0, 10), you want the following:

for comb in itertools.product(range(10), repeat=9): 

rather than combinations_with_replacement , or you’ll skip matrices like

numpy.array([[0, 1, 0], [0, 0, 0], [0, 0, 0]]) 

Источник

NumPy, часть 4: linalg

В прошлых частях мы разбирались с основными операциями над массивами и randomом в NumPy. Теперь же мы приступим к более серьёзным вещам, которые есть в NumPy. Первый на очереди у нас модуль numpy.linalg, позволяющий делать многие операции из линейной алгебры.

Возведение в степень

linalg.matrix_power(M, n) — возводит матрицу в степень n.

Разложения

linalg.cholesky(a) — разложение Холецкого.

linalg.qr(a[, mode]) — QR разложение.

linalg.svd(a[, full_matrices, compute_uv]) — сингулярное разложение.

Некоторые характеристики матриц

linalg.eig(a) — собственные значения и собственные векторы.

linalg.norm(x[, ord, axis]) — норма вектора или оператора.

linalg.cond(x[, p]) — число обусловленности.

linalg.det(a) — определитель.

linalg.slogdet(a) — знак и логарифм определителя (для избежания переполнения, если сам определитель очень маленький).

Системы уравнений

linalg.solve(a, b) — решает систему линейных уравнений Ax = b.

linalg.tensorsolve(a, b[, axes]) — решает тензорную систему линейных уравнений Ax = b.

linalg.lstsq(a, b[, rcond]) — метод наименьших квадратов.

linalg.inv(a) — обратная матрица.

• linalg.LinAlgError — исключение, вызываемое данными функциями в случае неудачи (например, при попытке взять обратную матрицу от вырожденной).
• Подробная документация, как всегда, на английском: https://docs.scipy.org/doc/numpy/reference/routines.linalg.html
• Массивы большей размерности в большинстве функций linalg интерпретируются как набор из нескольких массивов нужной размерности. Таким образом, можно одним вызовом функции проделывать операции над несколькими объектами.

Для вставки кода на Python в комментарий заключайте его в теги