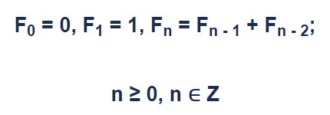Вычисление чисел фибоначчи java

Solving the Fibonacci problem using Dynamic Programming in Java

Today, I am going to give a tutorial on how to solve the Fibonacci problem using Dynamic Programming in Java. Before we start to talk about Dynamic Programming. I would like to start briefly on what the Fibonacci problem is. If you already know the problem. Feel free to skip to the next section.

Fibonacci problem

According to Wikipedia, “Fibonacci number are the numbers in the following integer sequence, called the Fibonacci sequence, and characterized by the fact that every number after the first two is the sum of the two preceding ones”

For example: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55

In modern usage, the sequence is extended by one more initial item: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55

In any given sequence of Fn, it often represent as,
Fn = Fn-1 + Fn-2, with seed value of F1=1, F2=1 or F0=0, F1=1 depends on your first initial value.

These are the values at the nth of the Fibonacci sequence.

0	1	2	3	4	5	6	7	8	9	10
0	1	1	2	3	5	8	13	21	34	55

For example, at the 8th of Fibonacci sequence is 21.

Okay, now that we have Fibonacci problem covered. Let’s talk about Dynamic Programming and how it can be useful to us to solve this problem.

Dynamic Programming

The basic idea of Dynamic Programming is to save the result of the subproblem so that if we see it again in the future. We can simply use it instead of recomputing the value again. In the long run, it should save some or a lot of time which reduces the running time complexity of the problem. (which is what you should always try to do when doing competitive programming questions)

Let’s take the simple example of the Fibonacci numbers: finding the nth Fibonacci number defined by Fn = Fn-1 + Fn-2 and F0=0, F1=1

The easiest and obvious way of doing this is to use the recursion:

Recursion

By using the caching technique or Memoization, we have eliminate the needed to recomputed a lot of numbers as you can see in the tree diagram above. Hence, the running time should be improved tons. However, the space complexity of the problem just got increased to O(N) as we created a HashMap to store the results of the value. (acting as cache) However, this is still not perfect. As you can see, number 7 has been asked 1 time. Number 6 has been asked 2 times. Number 5 has been asked 2 times. Number 4 has been asked 2 times. Rest of the number got asked twice except 0. The next question is, is it possible that all the number will get computed/asked once and we get what we want at the end?

Yes, it is totally possible. Let’s try it.

Bottom Up

A better way to do this is to get rid of the recursion all-together by evaluating the results in the right order. Instead of top down, we are going for bottom up.

 public HashMapInteger, Integer> hm = new HashMapInteger, Integer>(); public int getFibonacciNumberBottomUpWithCache(int n)  hm.put(0, 0); hm.put(1, 1); for(int i = 2; i  n; i++)  hm.put(i, hm.get(i - 1) + hm.get(i - 2)); > return hm.get(n); >

Now that we are going with the right direction. Each number in the sequence ONLY gets touch once. Hence, the running time should get further improved here compared with the top down approach. However, the next question is, do we really need to save the results to the cache? and waste another O(N) space. The answer here is not really. We can use constant space and store the only necessary partial results along the way:

 public int getFibonacciNumberBottomUpWithoutCache(int n)  if (n == 0 || n == 1) return n; int fnMin2 = 0; int fnMin1 = 1; int sum = 0; for(int i = 2; i  n; i++)  sum = fnMin1 + fnMin2; fnMin2 = fnMin1; fnMin1 = sum; > return sum; >

Here, the runnning time for this approach should stay O(N) like above using the cache. However, we greatly reduced the space complexity from O(N) to O(1) constant space. Both running time and space complexity optimized.

Tada. You have done it using the Dynamic Programming way=)

Wrapping Up

This tutorial is largely based on a StackOverflow post by Tristan.

His idea of applying the Dynamic Programming is as follows:

• Find the recursion in the problem.
• Top-down: store the answer for each subproblem in a table to avoid having to recompute them.
• Bottom-up: Find the right order to evaluate the results so that partial results are available when needed.

Notes from his as well: Dynamic programming generally works for problems that have an inherent left to right order such as strings, trees or integer sequences. If the naive recursive algorithm does not compute the same subproblem multiple time, dynamic programming won’t help.

In case you want to run the live example, click the link here.

Hopefully this guide has help you to solve the Fibonacci problem using the Dynamic Programming. Thank you for reading!

Resources

I’ll try to keep this list current and up to date. If you know of a great resource you’d like to share or notice a broken link, please let us know.

Getting started

Share

PoAn (Baron) Chen

Software Engineer at Microsoft. Graduated from @uvic. Previously worked at @illumina, @ACDSee, @AEHelp and @AcePersonnel1. My words are my own.

Comments

Disclaimer: the theme of the site is largely based on will-jekyll-template by Willian Justen

Источник

Что должен знать программист на Java о числах Фибоначчи

Часто на собеседованиях, особенно в иностранных компаниях, могут расспрашивать об алгоритмах, а в стрессовой ситуации судорожно что-то вспоминать бывает не всегда просто. Поэтому нужно готовиться. Для начала, хотя бы освежить в памяти основные алгоритмы. Сегодня мы разберем такое явление как числа Фибоначчи и наиболее встречаемые варианты задач, связанных с ними. Числа Фибоначчи — это последовательность натуральных чисел, которая начинается с чисел ноль и один, а каждое последующее число равно сумме двух предыдущих:

Стоит отметить, что иногда 0 опускается, и ряд начинается с 1 1 2 3… Как правило в условиях задачи сразу уточняется, с каких первых двух чисел начинается ряд (0,1 или 1,1), поэтому дальше мы будем рассматривать решения для обоих случаев.

Получение первых n чисел Фибоначчи в Java

 int[] arr = new int[n]; arr[0] = 0; arr[1] = 1; for (int i = 2; i

Мы создаём массив размера n. Первые два элемента будут равны нулю и единице, а остальные элементы получаем, проходясь по данному циклу и используя предыдущие числа из массива. И выводим на экран:

 int[] arr = new int[n]; arr[0] = 1; arr[1] = 1; for (int i = 2; i

Всё, что нам нужно было изменить — это первый элемент массива arr[0]: с 0 на 1. Соответственно, первые 10 элементов будут:

Первые n чисел Фибоначчи через stream

 Stream.iterate(new int[], arr -> new int[]) .limit(n) .map(y -> y[0]) .forEach(x -> System.out.println(x)); 

Статический метод iterate класса Stream возвращает бесконечный упорядоченный поток, созданный применением функции к начальному массиву arr. В нашем случае в качестве функции служит задание правила составления каждого нового массива, основываясь на предыдущем. Как итог мы получим поток из массивов:

Но их будет бесконечное количество, и поэтому с помощью .limit(n) мы урезаем количество элементов до первых n (в нашем случае до 10). Однако нам не нужен поток массивов, поэтому с помощью .map(y -> y[0]) мы отбираем по первому элементу каждого массива и получаем поток с необходимыми нам числами и с помощью forEach выводим на консоль. Выглядит покруче, не так ли? при первых элементах 1,1 этот код также будет почти таким же:

 Stream.iterate(new int[], arr -> new int[]) .limit(n) .map(y -> y[0]) .forEach(x -> System.out.println(x)); 

Сумма чисел Фибоначчи

 int n = 10; int result = Stream.iterate(new int[], arr -> new int[]) .limit(n) .map(t -> t[0]) .mapToInt(Integer::intValue) .sum(); System.out.println(result); 

Получение n-ого число в ряде Фибоначчи

 public int getFibonacciValue(int n) < if (n else if (n == 2) < return 1; >else < return getFibonacciValue(n - 1) + getFibonacciValue(n - 2); >> 

 public int getFibonacciValue(int n) < if (n == 0) < return 0; >else if (n == 1) < return 1; >else < return getFibonacciValue(n - 1) + getFibonacciValue(n - 2); >> 

В этом случае нам достаточно задать только первый элемент как 1, так как второй элемент будет таким же, и реакция метода будет такой же. При этом мы задаём реакцию метода на 0, ведь если не задать, то когда придёт 2 как аргумент, рекурсивно вызывается этот же метод, но с аргументом 0. Далее будет запускаться этот же метод, но уже с отрицательными числами и так до отрицательной бесконечности. Как итог мы получим StackOverflowError.

Тем не менее, рекурсивный способ не рекомендуется использовать, потому что в отличие от предыдущих способов, которые работают за линейное время от O(n), рекурсивный способ может работать значительно дольше. Почему? Рекурсивный способ может работать долго, так как в процессе расчёта функция будет много раз вызываться от одного и того же аргумента. Например, при вычислении getFibonacciValue(7) функция сделает рекурсивные вызовы к getFibonacciValue(5) и getFibonacciValue(6), оба рекурсивных вызова будут обращаться к getFibonacciValue(4)), что и приведёт к многоразовому вызову одних и тех же операций. На собеседовании можно показать этот способ как вариант решения, но при этом рассказать об этих его недостатках и взамен предложить другой способ. Также стоит отметить, что тип int в Java позволяет хранить от -2147483648 до 2147483647, поэтому получится вычислить только первые 46 чисел Фибоначчи: при попытке получить следующее 47-ое возникнет переполнение, и мы получим отрицательное число. Если же мы будем использовать тип данных long вместо int, то получится правильно вычислить первые 91 число Фибоначчи. Чтобы вычислять последующие числа Фибоначчи, необходимо воспользоваться классом BigInteger, который реализует логику хранения и арифметических операций действительно БОЛЬШИХ чисел.

Источник

Вычисление чисел Фибоначчи

Числа Фибоначчи — это числа такой последовательности, в которой первые два элемента — 0 и 1, а каждый последующий элемент равен сумме двух предшествующих. Выглядит это так:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …

Примечание Иногда 0 опускается, и в этом случае ряд начинается с 1, но мы будем использовать последовательность с 0 на первой позиции.

Формула записывается следующим образом:

Вычисление ряда Фибоначчи — стандартная задача, которую задают на собеседованиях, чтобы проверить кандидата на понимание алгоритмов. Не так популярна, как сортировка, но всё же.

Давайте вычислим ряд и его отдельные элементы, использовав для этого язык Java.

Вычислить ряд Фибоначчи циклом

Предположим, что нам нужно вывести на экран первые десять чисел последовательности Фибоначчи. Мы помним, что:

Тогда наша последовательность будет иметь такой вид:

Но нам нужно вывести результат с использованием программы. Держите код с объяснениями в комментариях:

Выполнение завершится на десятом элементе. Количество элементов при этом можно менять, изменив значение в условиях цикла.

Найти число Фибоначчи через рекурсию

Рекурсивная функция — это такая функция, которая вызывает саму себя. Она также неплохо отрабатывает в алгоритмических задачах вроде чисел Фибоначчи, но ей требуется больше времени.

Почему так происходит? Всё дело в том, что рекурсивная функция приводит к многоразовому вызову одних и тех же операций. Именно из-за этого её не рекомендуется использовать, но если уж на собеседовании прозвучит такая задача, вы будете готовы.

Рассмотрим пример, в котором нам нужно получить n-ое число в ряде Фибоначчи:

public int fibonacciValue(num) < if (num else if (num == 2) < return 1; >else < return fibonacciValue(num - 1) + fibonacciValue(num - 2); >>

Если в качестве num задать большое значение, программа зависнет.

Тип int в Java может хранить значения до 2147483647, так что вычислить получится лишь первые 46 чисел Фибоначчи. Тип long хранит до 9223372036854775807, а это 91 число Фибоначчи. Класс BigInteger призван работать с действительно большими значениями, вот только само выполнение программы это никак не ускорит.

Использовать для вычисления Stream

Stream в Java — это компонент для самостоятельной внутренней итерации своих же элементов. Подробнее о нём вы можете почитать в нашей статье о Java Stream API.

И, разумеется, Stream подходит для вычисления элементов последовательности Фибоначчи:

Stream.iterate(new int[], arr -> new int[]) //Задаём лимит значений: .limit(num) //Отбираем по первому элементу каждого массива: .map(y -> y[0]) //Выводим в консоль: .forEach(x -> System.out.println(x));

В данном примере метод iterate() будет возвращать упорядоченный поток, ограниченный лимитом в num значений и созданный с применением функции к начальному массиву arr . В консоль будет выведено следующее:

А так мы получим сумму чисел последовательности по элемент num включительно:

int fibonacciValuesSum = Stream.iterate(new int[], arr -> new int[]) .limit(num) .map(y -> y[0]) .mapToInt(Integer::intValue) .sum(); System.out.println(fibonacciValuesSum);

Математический тест

Любите математику? Попробуйте решить наш математический тест:

Источник