Алгоритмическая сложность
Алгоритмическая сложность — тема отдельного курса в классических университетских программах. Как, впрочем, и математический анализ. Однако на собеседовании Вас вряд ли попросят посчитать интеграл, а вот про сложность алгоритмов спрашивают практически всех на любую позицию программиста. А знакомо ли Вам понятие алгоритмическая сложность? А какая сложность быстрой сортировки? А это в лучшем или в худшем случае? Бывает, с горем пополам разобрались с какой-нибудь задачей на логику, но вас добивают: а какая сложность Вашего решения, можно ли ускорить? В этом посте постараюсь объяснить, что тут к чему, и не пугайтесь, если для Вас NP-полнота значит не больше, чем NP-пустота.
Важность понятия алгоритмической сложности в том, что на практике, как правило, существует разумно оптимальный способ решить задачу. Использовав его, дальнейшая оптимизация будет улучшать производительность на 10-50%, что потребует ещё в два или пять раз больше времени на разработку. Одновременно с этим, неправильно выбранный способ решения будет работать медленнее в десять, в сто, в тысячу раз. На практике система виснет на простых операциях, загрузка занимает секунды, а всевозможные запланированные задачи запускаются по ночам и работают часами. И объёмы данных отнюдь не терабайты, достаточно нескольких миллионов записей. И я расскажу, почему.
Сложность алгоритма — это ответ на вопрос сколько действий придётся совершить, чтобы решить задачу, в зависимости от параметров задачи. Разнородных параметров в задаче может быть много, и разнородных действий тоже. И то и другое нужно сократить до одного: один параметр и одно действие, остальное отбросить. Например, Вы листаете договор из тысячи страниц и подписываете каждую. Входной параметр такой задачи будет количество страниц, а действие — поставить подпись. Перелистывание страниц мы не считаем за важное действие, потому что это намного быстрее подписи. Не важно, сколько времени уйдёт на всё, два часа или два дня — кто-то расписывается быстрее, кто-то медленнее. Но каждому потребуется 1000 действий для выполнения алгоритма. Если обобщить, то требуется N действий при N страницах. Легко можно посчитать, что если Вы подписали договор из 10 страницы за 10 минут, то на 60 страниц Вы потратите час. Если оптимизировать процесс и подписывать только первую страницу, то потребуется одна минута вне зависимости от количества страниц.
Другой пример — на бумаге разлинован квадрат со стороной 10. В каждой клетке нужно поставить точку, всего точек 100 (N^2). Если потребовалось 10 минут на всё про всё, то, чтобы повторить алгоритм на квадрате со стороной 60, потребуется 10 / 100 * 60 * 60 = 360 минут, то есть 6 часов. Итого в одной задаче увеличив входной параметр в шесть раз, мы потратили в 6 раз больше времени, а в другой — в 36. Разница колоссальная.
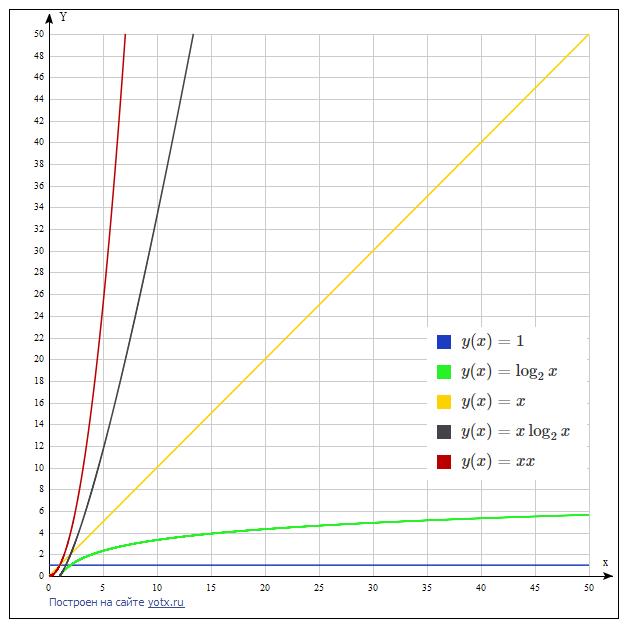
Я привёл три примера сложности алгоритма: константную, порядка N и порядка N^2. У программистов принято говорить «О большое от». Ниже для порядка я приведу строгое определение, но на практике требуется лишь указать порядок скорости роста времени работы алгоритма при росте основного параметра задачи. Коэффициент перед функцией от N не важен: если требуется N^2 действие или 100 * N^2 действий — это всё равно будет O(N^2), потому что в обоих случаях рост N в два раза увеличивает время работы в четыре.
«O»-обозначение используется, если нужно определить асимптотическую верхнюю границу для функции f(n), равную времени работы алгоритма в зависимости от основного параметра задачи.
//before java8 for (IteratorString> iterator = elements.iterator(); iterator.hasNext(); ) String next = iterator.next(); if(Long.parseLong(next) % 2 == 1) iterator.remove(); > > Но на собеседованиях часто даются такие задачи с небольшим подвохом, чтобы проверить понимание нюансов. Решения исходной задачи:
//java8 AtomicInteger counter = new AtomicInteger(0); elements.removeIf(s -> counter.incrementAndGet() % 2 == 0); //before java8 int counter = 0; for (IteratorString> iterator = elements.iterator(); iterator.hasNext(); ) iterator.next(); if (counter++ % 2 == 1) iterator.remove(); > > //before java8 //хитрый способ избежать введения переменной counter. Следует избегать таких неочевидных приёмов. for (ListIteratorString> literator = elements.listIterator(elements.size()); literator.hasPrevious();) literator.previous(); if (literator.previousIndex() % 2 == 0) literator.remove(); > > //O(n) for ArrayList //решение на крайний случай, если вероятны проблемы с производительностью, но от ArrayList не уйти. //объём кода не соответствует сложности задачи, читаемость его тоже низкая, придётся объяснять в комментариях, //почему так, а не иначе //если применить это решение к LinkedList, то получим O(n^2) removeFromArrayList(elements, i -> i % 2 == 1); static void removeFromArrayList(ArrayListString> elements, IntPredicate removeIf) int lastIndex = 0; for (int i = 0; i elements.size(); i++) if (!removeIf.test(i)) elements.set(lastIndex, elements.get(i)); lastIndex++; > > int extraElementsCount = elements.size() - lastIndex; //unfortunately, we can't use protected removeRange method for (int i = 0; i extraElementsCount; i++) elements.remove(elements.size() - 1); > > Прокомментирую решения, предложенные на stackoverflow.
//1. //Корректное решение. O(n^2) для ArrayList, O(n) для LinkedList int i = 0; for (IteratorString> it = words.iterator(); it.hasNext(); ) it.next(); // Add this line in your code if (i % 2 != 0) it.remove(); > i++; > //2. //Некорректное решение. O(n^2) для ArrayList, O(n^2) для LinkedList. //Ошибочный результат при дублирующихся значениях в списке. int i = 0; ListString> list = new ArrayListString>(); for (String word:words) if (i % 2 != 0) //it.remove(); list.add(word); > i++; > words.removeAll(list); //элементы удаляются по значению! //додумать решение можно так (ещё заменить условие на ==0): //words.clear(); //words.addAll(list); //3. //На этом примере я потерпел фиаско. Я был уверен, что код не работает, потому что размер и индексы будут изменяться по ходу работы алгоритма, //что, удаляя элемент с индексом 2, мы удаляем элемент с индексом 3 в исходном массиве. Всё перепуталось и не может дать верный результат. //Но! результат верный. На каждом шагу мы удаляем элемент, сдвигаем все индексы на 1 влево, но увеличиваем счётчик на 1, а не на 2. //здесь мои полномочия всё, как говорится //Сложность O(n^2) для ArrayList и LinkedList int i = 1; while (i words.size()) words.remove(i++); > //4. //Корректное решение. Единственное из предложенных O(n) для ArrayList; O(n^2) для LinkedList. //Минус - тяжело читаемый код. Два счётчика, называются i, j. Причём j всегда равно i/2. //Если это писали не Вы, то придётся запускать отладку, чтобы разобраться. int j = 0; for(int i = 0 ; i integers.size(); i++) if( i % 2 == 0) integers.set(j, integers.get(i)); j++; > > int half = integers.size()%2==0 ? integers.size()/2 : integers.size()/2 + 1; integers.subList(half , integers.size()).clear();//буду знать, что subList не создаёт новый список, а лишь ссылку на подсписок текущего. //поэтому хвост можно обрезать вот так в одну строчку. Пример с удалением один из самых базовых и простых. Подобным образом можно мусолить любые коллекции и операции с ними: LinkedList, ArrayList, HashMap, TreeMap, LinkedHashMap, CopyOnWriteArrayList и так далее. В данном посте я этого делать не буду, перейду к итогу всего что я тут понаписал.
Заключение
Приходится соблюдать тонкий баланс между оптимальностью решения по производительности, читаемостью и лаконичностью кода и здравым смыслом. Главное понимать насколько быстро можно решить типовую задачу и подобрать правильные структуры данных и операции с ними. На интервью на позицию Java разработчика часто вопрос по данной тематике будет вторым (после «методов класса Object» или «расскажите о последнем проекте»).