Симплексный метод решения задач линейного программирования
Симплексный метод – это метод последовательного улучшения плана. Этим методом можно решать задачи линейного программирования с любым количеством переменных и ограничений.
Этот метод включает в себя три основные этапа:
- Построение начального опорного плана.
- Правило перехода к лучшему (точнее, нехудшему) решению.
- Критерий проверки найденного решения на оптимальность.
1) Построение начального опорного плана.
Данную задачу линейного программирования необходимо сначала привести к каноническому виду; при этом правые части ограничений должны быть неотрицательными. Признаком возможности построения начального опорного плана служит наличие в каждом ограничении-равенстве с неотрицательной правой частью базисной переменной. Базисной называют плановую переменную, которая входит только в одно уравнение (а в другие не входит), и при этом имеет коэффициент, равный единице. Пусть задача линейного программирования приведена к каноническому виду, и все уравнения системы ограничений имеют свою базисную переменную. Приравняв базисные переменные к соответствующим правым частям ограничений, а остальные переменные к нулю, получим опорное или базисное решение задачи. Пример. Для данной задачи линейного программирования найти начальный опорный план (базисное решение). 


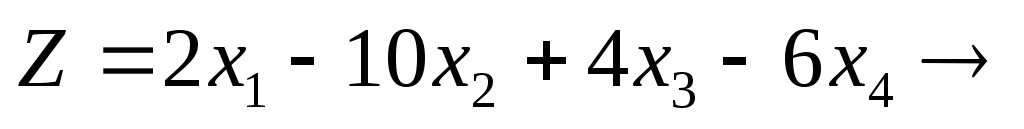
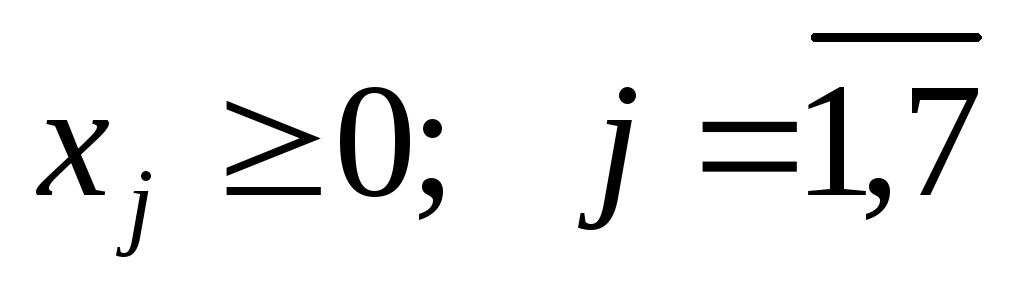




2) Составление симплексных таблиц. Критерий оптимальности.
Симплексный метод удобно применять, используя построение симплексных таблиц. Первая симплексная таблица, соответствующая начальному плану, имеет вид:
| Базис |  | В |  |  | … |  |  |
 |  | … | 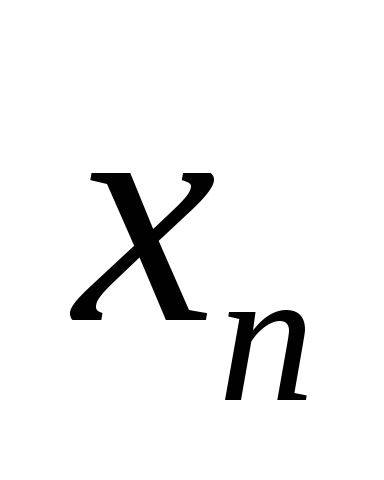 | ||||
 |  |  |  |  | … |  | |
 |  | 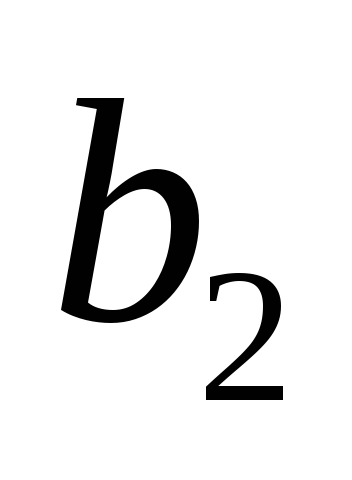 |  | 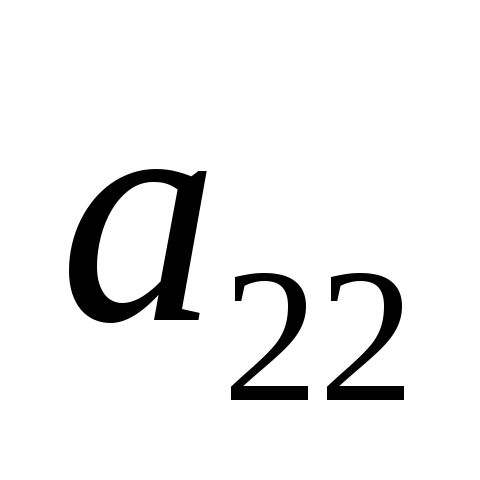 | … |  | |
| … | … | … | … | … | … | … | |
 |  | 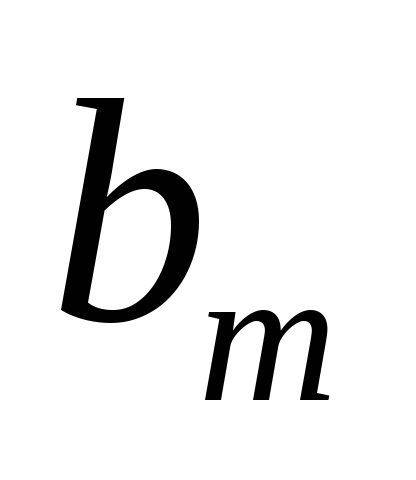 |  |  | … | 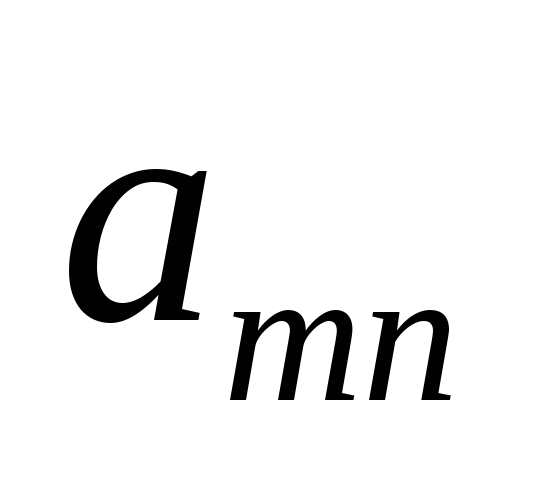 | |
 |  |  |  | … |  | ||
Здесь приняты следующие обозначения. Столбец «Базис» – это базисные переменные. Столбец «









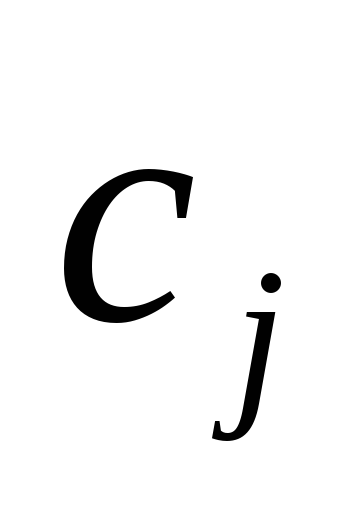










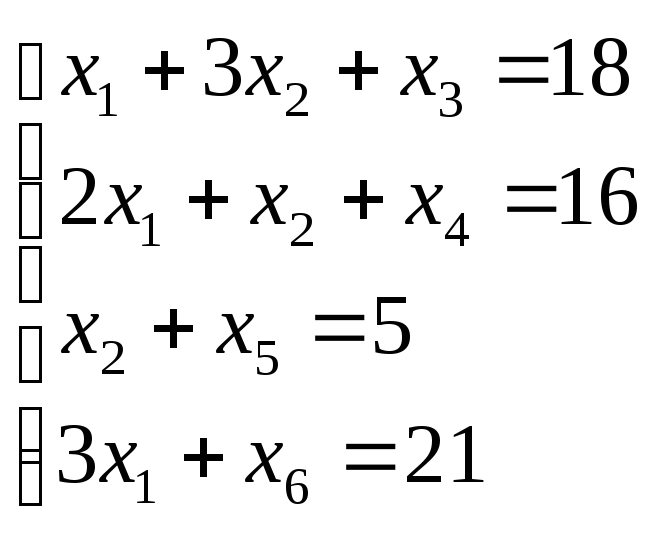



| Базис | 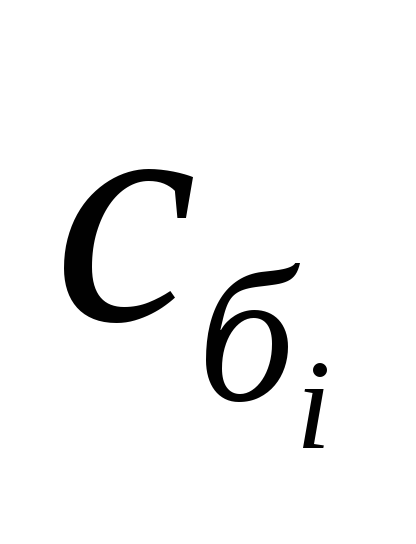 | В | 2 | 3 | 0 | 0 | 0 | 0 |  |
 |  |  |  | 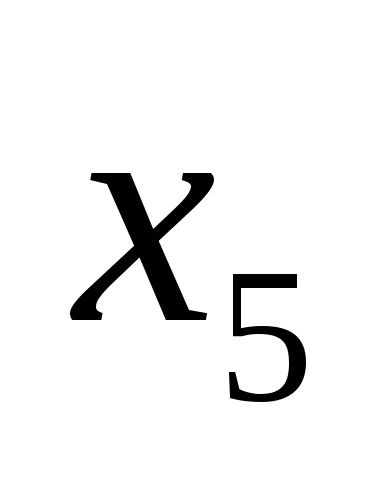 |  | ||||
 | 0 | 18 | 1 | 3 | 1 | 0 | 0 | 0 | 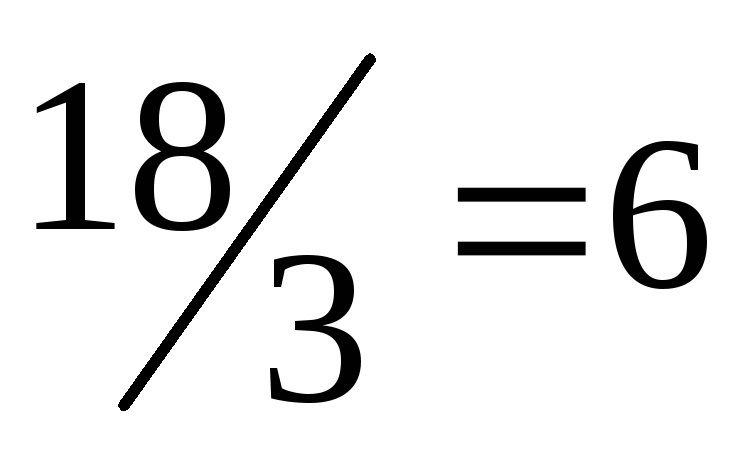 |
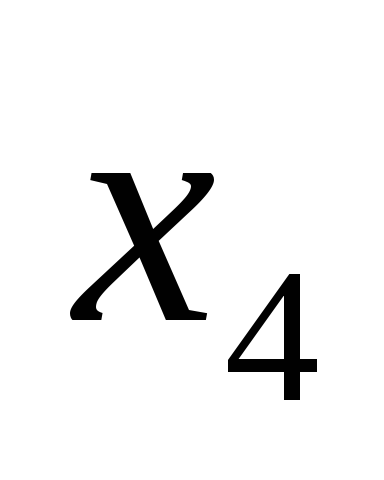 | 0 | 16 | 2 | 1 | 0 | 1 | 0 | 0 | 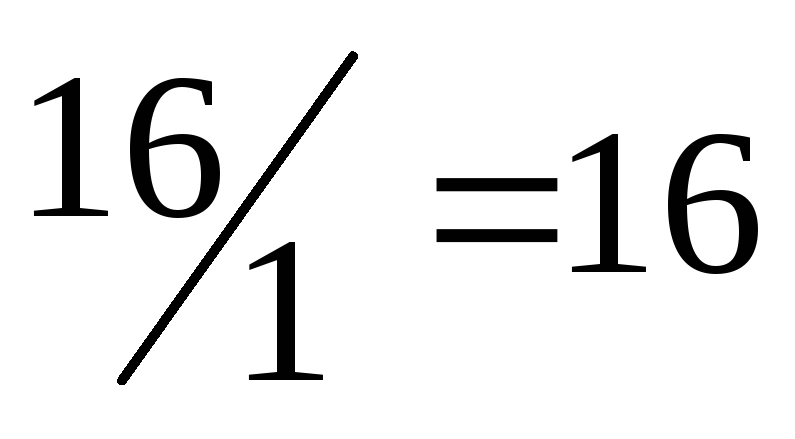 |
 | 0 | 5 | 0 | 1 | 0 | 0 | 1 | 0 |  |
 | 0 | 21 | 3 | 0 | 0 | 0 | 0 | 1 | – |
 |  0 0 |  –2 –2 |  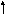 –3 –3 |  0 0 |  0 0 |  0 0 |  0 0 | ||
Здесь 







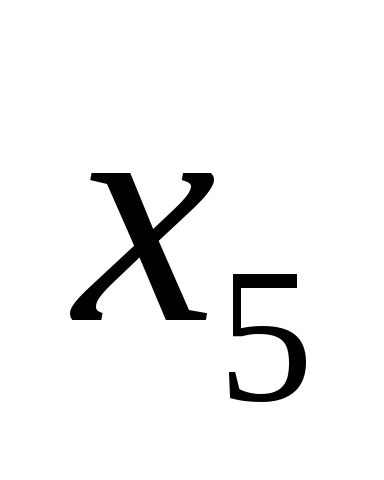

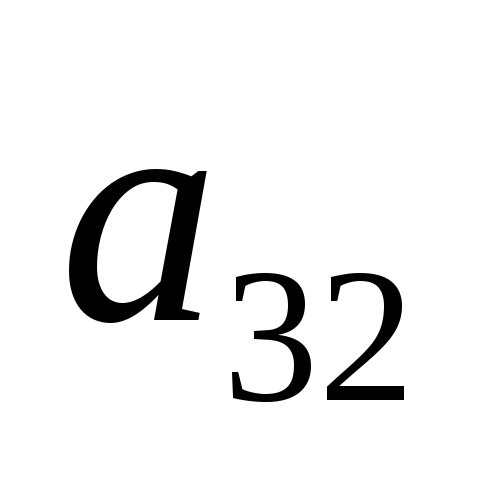
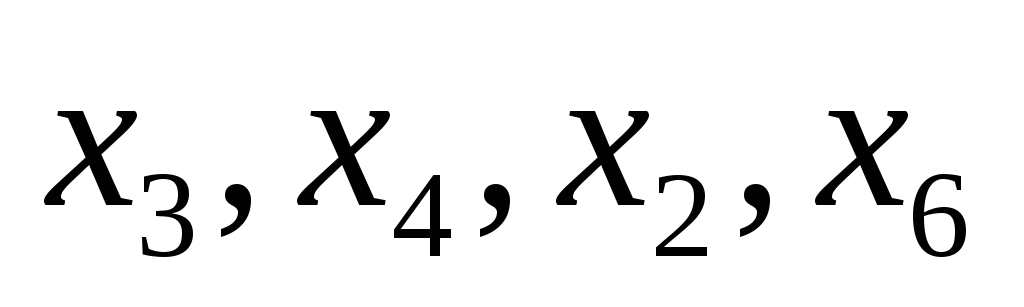




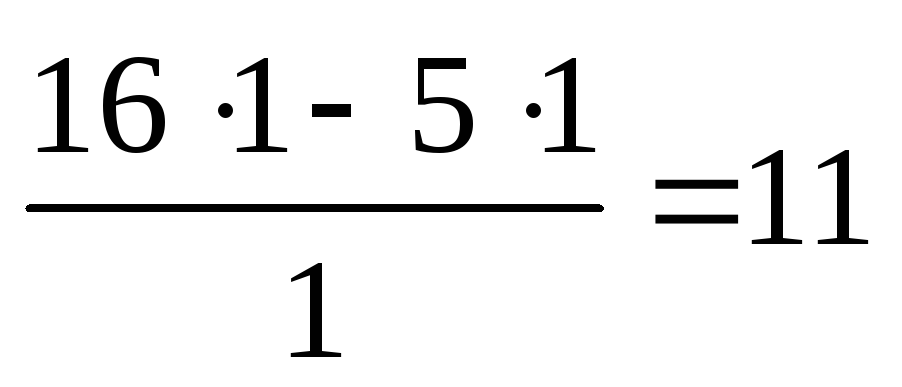



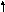
| Базис | 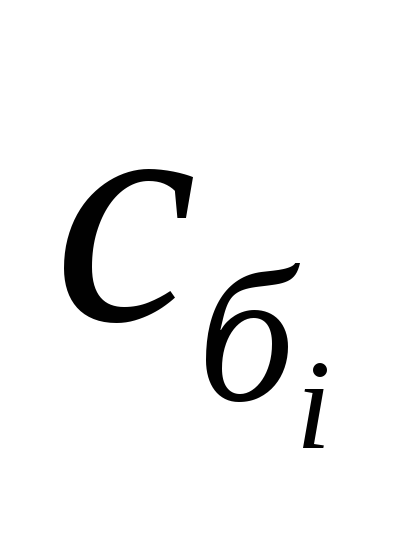 | В | 2 | 3 | 0 | 0 | 0 | 0 |  |
 | 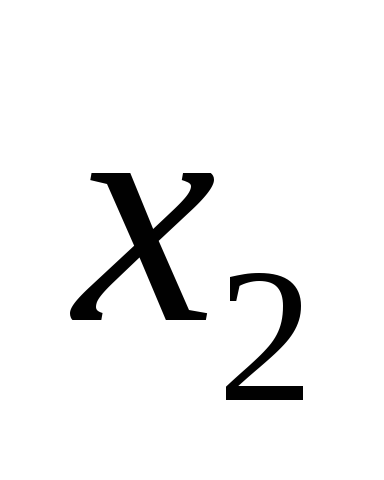 |  |  |  |  | ||||
 | 0 | 18 | 1 | 3 | 1 | 0 | 0 | 0 | 6 |
 | 0 | 16 | 2 | 1 | 0 | 1 | 0 | 0 | 16 |
 | 0 | 5 | 0 | 1 | 0 | 0 | 1 | 0 | 5 |
 | 0 | 21 | 3 | 0 | 0 | 0 | 0 | 1 | – |
 | 0 | –2 | –3 | 0 | 0 | 0 | 0 | таб. 1 | |
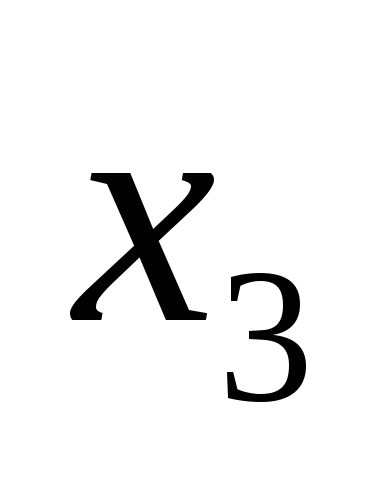 | 0 | 3 | 1 | 0 | 1 | 0 | –3 | 0 | 3 |
 | 0 | 11 | 2 | 0 | 0 | 1 | –1 | 0 | 5,5 |
 | 3 | 5 | 0 | 1 | 0 | 0 | 1 | 0 | – |
 | 0 | 21 | 3 | 0 | 0 | 0 | 0 | 1 | 7 |
 | 15 | –2 | 0 | 0 | 0 | 3 | 0 | таб. 2 | |
| Базис | 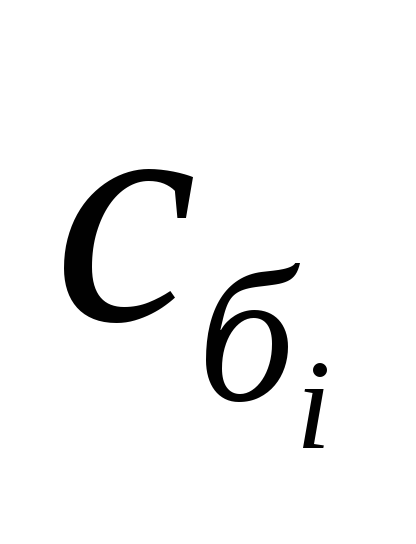 | В | 2 | 3 | 0 | 0 | 0 | 0 |  |
 |  |  |  | 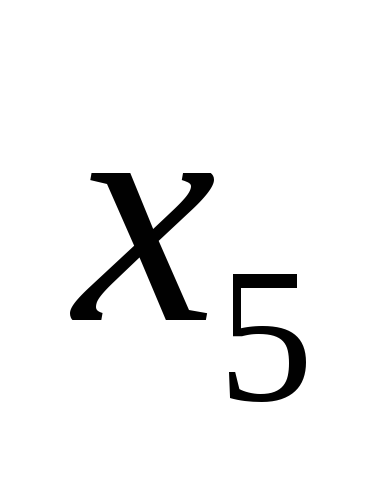 |  | ||||
 | 2 | 3 | 1 | 0 | 1 | 0 | –3 | 0 | – |
 | 0 | 5 | 0 | 0 | –2 | 1 | 5 | 0 | 1 |
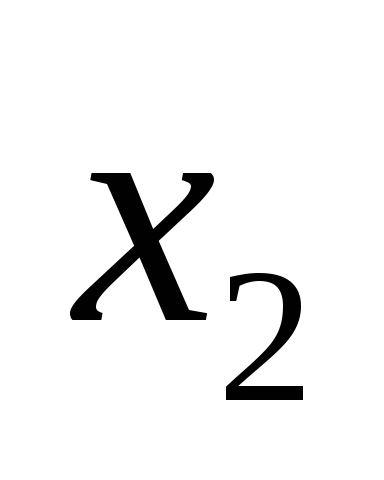  | 3 | 5 | 0 | 1 | 0 | 0 | 1 | 0 | 5 |
 | 0 | 12 | 0 | 0 | –3 | 0 | 9 | 1 |  |
 | 21 | 0 | 0 | 2 | 0 | –3 | 0 | таб. 3 | |
 | 2 | 6 | 1 | 0 | –0,2 | 0,6 | 0 | 0 | |
 | 0 | 1 | 0 | 0 | –0,4 | 0,2 | 1 | 0 | |
 | 3 | 4 | 0 | 1 | 0,4 | –0,2 | 0 | 0 | |
 | 0 | 3 | 0 | 0 | 0,6 | –1,8 | 0 | 1 | |
 | 24 | 0 | 0 | 0,8 | 0,6 | 0 | 0 | таб. 4 | |
О













| а) | 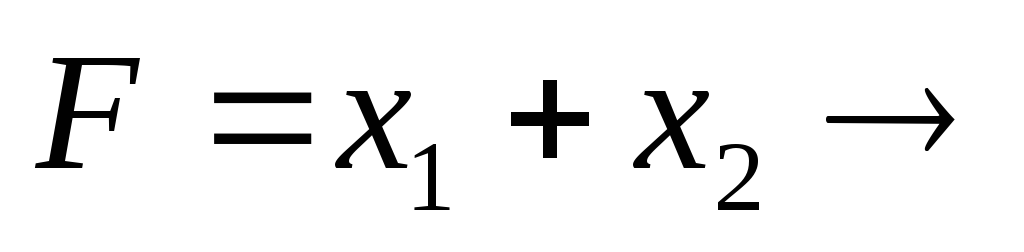 max max 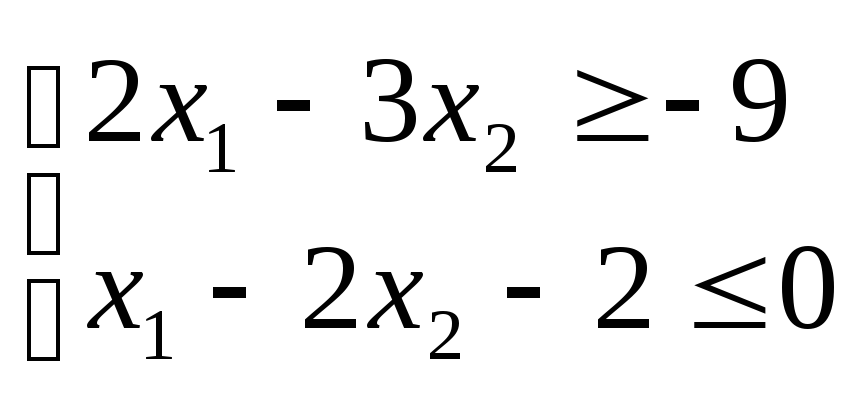 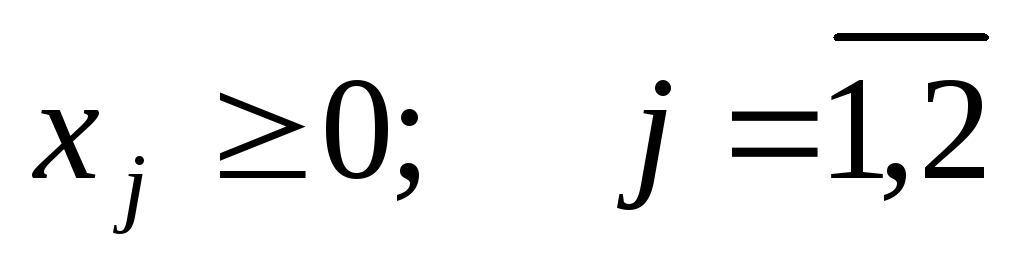 | б) |  min min   |
3.2. Симплекс-метод решения задач линейного программирования
Поскольку, как было показано в п. 3.1 решение задачи линейного программирования находится в одной из крайних (угловых) точек ОДЗ, важным вопросом является изучение не системы неравенств (4), а соответствующей системы уравнений AX = B, решение которой дает угловые точки ОДЗ.
Если уравнения системы АX = B линейно независимы, то система имеет множество решений при n > m и единственное решение при n = m. При решении задачи линейного программирования симплекс-методом всегда будет выполняться n > m, поэтому для получения некоторого одного решения, «лишние» n – m переменных приравниваются нулю.
Если приравнять к нулю n – m произвольных переменных (например, переменные xm+1, xm+2, …, xn) и, решив систему, найти значения оставшихся m переменных (x1, x2, …, xm), то такое решение называется базисным.
Если нулю приравнять некоторые другие n – m переменных – получим другое базисное решение. Любое базисное решение, у которого все переменные неотрицательные называется допустимым базисным решением.
Переменные, которые были приравнены нулю, называются небазисными. Оставшиеся т переменных, значение которых получены из решения системы, называются базисными.
Допустимое базисное решение представляет собой угловую вершину ОДЗ.
Решение задачи симплекс-методом сводится к направленному перебору смежных друг с другом угловых точек, которые представляют собой допустимые базисные решения.
Сформулируем в общем виде алгоритм симплекс-метода:
1: Приведение задачи к стандартной форме. Стандартной формой задачи линейного программирования будем называть задачу, у которой все ограничения записаны как равенства и при этом правые части ограничений неотрицательны.
2: Выделение исходного базисного решения (по возможности из стандартной формы). То есть определение тех переменных n – m переменных, которые приравниваются нулю и нахождение значений оставшихся базисных переменных.
3: Определение, является ли полученное базисное решение оптимальным, если да, то решение окончено, иначе переходим к шагу 4.
4: Определение переменной, которая войдет в базис и переменной, которая из базиса выйдет таким образом, чтобы новое решение было лучше предыдущего. То есть, если текущее базисное решение неоптимально, необходимо определить, какую из базисных переменных приравнять нулю, и какую из небазисных переменных вместо нее включить в базис.
5: Использование эквивалентных преобразований методом Жордана-Гаусса для нахождения нового допустимого базисного решения. Переход к шагу 3.
Чтобы привести задачу линейного программирования к стандартной форме необходимо:
1. Убедиться, что во всех ограничениях правые части bi неотрицательны. Если есть отрицательные правые части ограничений, такие ограничения нужно умножить на –1 (при этом учесть, что в ограничениях типа или знак ограничения изменится на противоположный).
2. К левой части ограничений типа нужно прибавить новую, дополняющую переменную S, которая уравнивала бы левую и правую часть и показывала бы насколько левая часть ограничения меньше правой.
в стандартном виде будет выглядеть так:
3. Из левой части ограничений типа нужно вычесть новую, избыточную переменную e, которая уравнивала бы левую и правую часть и показывала бы насколько левая часть ограничения больше правой.
в стандартном виде будет выглядеть так:
Дополняющие переменные S и избыточные e будем называть вспомогательными, в то время, как переменные x – основными.
Чтобы из стандартной формы сразу выделить базисное решение, необходимо в качестве базисных переменных выбрать те m переменных, каждая из которых встречается только в одном из уравнений и включена в него с коэффициентом, равным единице.
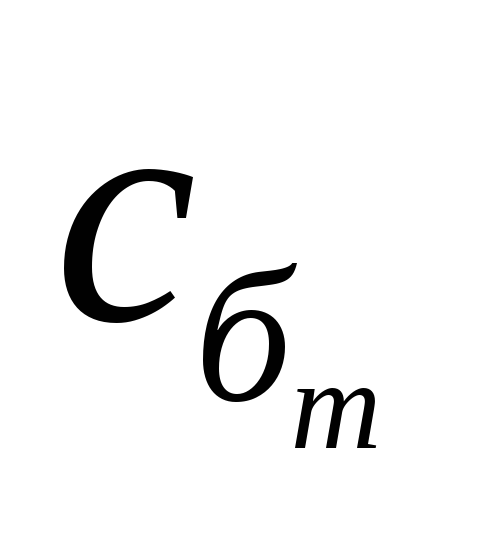
В качестве исходных базисных переменных в задачах с ограничениями удобно брать переменные S1, …, Sn.
Реализацию алгоритма симплекс-метода проиллюстрируем на следующем примере.
Пример 3.2. Мебельная фабрика может производить шкафы, столы, стулья. При изготовлении мебели используются древесина, труд рабочих на столярном и отделочном участках. Необходимое количество ресурсов для изготовления шкафов, столов и стульев приведено в таблице:
Таблица 3.1 – Исходные данные к примеру 3.2

