Вектор градиента при решении задачи линейного программирования геометрически

1.3. Геометрическая интерпретация и графический метод решения злп

В теории линейного программирования существуют две геометрические интерпретации решения ЗЛП. Первая интерпретация применяется для ЗЛП, записанной в стандартной форме, вторая – для ЗЛП, записанной в канонической форме.

Сначала рассмотрим с геометрической точки зрения представление множества допустимых планов стандартной ЗЛП на плоскости. Пусть количество ограничений m есть произвольное число, а количество переменных n равно 2. Тогда система ограничений ЗЛП в стандартной форме записи будет выглядеть следующим образом:

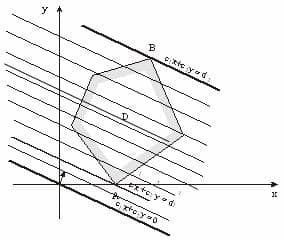
Каждое из неравенств системы ограничений (1.17) и (1.18) представляет в пространстве переменных x₁ и x₂ полуплоскость с границей, определяемой уравнением прямой , x₁ = 0, x₂ = 0. Если система неравенств (1.17) с учетом условия (1.18) совместна, тогда пересечение всех этих полуплоскостей геометрически представляет многоугольник возможных решений системы, а именно – множество допустимых планов рассматриваемой задачи.

В линейном программировании множество допустимых планов с геометрической точки зрения может представлять собой:

• выпуклый ограниченный многогранник;
• выпуклый неограниченный многогранник;
• пустое множество.

Графический метод решения злп

Рассмотрим ЗЛП с двумя переменными x₁, x₂ и m условиями-неравенствами:

При этом может быть наложено ограничение на переменные:

Предположим, что множество допустимых планов ЗЛП (1.19) – (1.21) представлено в виде пятиугольника (рис. 1.5). Прямые, высекающие многоугольник OABCE на плоскости x₁Ox₂, определяются условиями (1.20) при m = 3 и (1.21), в которых знаки неравенства заменены на знаки равенства. Штриховка указывает общую часть пересечения полуплоскостей.

В этом многоугольнике необходимо найти такую точку, которая доставляла бы, например, максимум целевой функции (1.19). Поведение целевой функции может быть охарактеризовано с помощью линии уровня.

Определение 9. Линией уровня функции называется множество точек из области ее определения, в которых функция принимает одно и то же фиксированное значение.

Для нашего случая линия уровня определяется уравнением . Линия уровня, проходящая через начало координат, имеет вид .

C(x) = const

Рис. 1.5. Графическая иллюстрация решения ЗЛП

Определение 10. Градиентом функции f (x) = f (x₁, x₂,…, x_n) называется вектор , указывающий направление наиболее быстрого возрастания функции.

Для линейной функции двух переменных линия уровня представляет собой прямую линию, перпендикулярную градиенту С(x):

Градиент показывает направление возрастания целевой функции.

Таким образом, с геометрической точки зрения решение ЗЛП сводится к определению такой точки множества допустимых планов D, через которую проходит линия уровня, соответствующая наибольшему из возможных значений. Это означает, что для нахождения точки максимума необходимо построить линию уровня для некоторого произвольного значения целевой функции, например, нуля. Затем следует осуществлять ее параллельное перемещение так, чтобы она оставалась перпендикулярной вектору С(Х) до тех пор, пока не достигнет такой точки области D, из которой дальнейшее смещение в направлении вектора С(Х) было бы невозможно (выходим из области D).

Аналогично осуществляется поиск минимума целевой функции. Однако при этом движение по линиям уровня должно производится в направлении, обратном градиенту, т.е. по вектору –С(Х). Такой метод решения ЗЛП называется графическим.

На рис. 1.5 изображен некоторый частный случай, для которого решение ЗЛП (максимум целевой функции) достигается в точке C области D. Вообще возможны следующие варианты решения ЗЛП геометрическим методом.

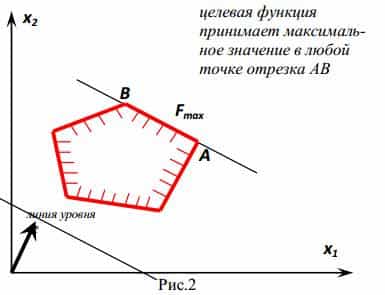
На рис. 1.6 изображен случай, когда максимальное значение целевая функция принимает в любой точке отрезка BL. В этом случае линия уровня при перемещении в сторону увеличения значения целевой функции сливается с отрезком BL. Оптимальных планов будет бесконечное множество.

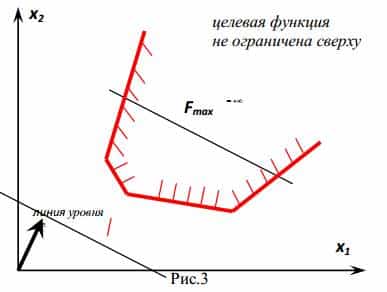
Аналогично, рис. 1.7 показывает, что оптимальными планами ЗЛП являются все точки луча AB. Рисунок 1.8 иллюстрирует ситуацию неограниченности целевой функции на множестве допустимых планов D, т.е. сколько бы мы ни перемещались по линиям уровня в направлении градиента, ее значение будет возрастать. Если же область допустимых планов состоит из одной единственной точки, то она является и оптимальным планом.

Отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.

С(x) K С(x) N

0 x₁ 0 M x₂

Рис. 1.6. Оптимальные планы Рис. 1.7. Оптимальные планы

отрезок BL луч AB

Источник

Графический метод решения ЗЛП

В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений (см. рисунок).

Инструкция . Выберите количество строк (количество ограничений). Если количество переменных больше двух, необходимо систему привести к СЗЛП (см. пример и пример №2). Если ограничение двойное, например, 1 ≤ x₁ ≤ 4 , то оно разбивается на два: x₁ ≥ 1 , x₁ ≤ 4 (т.е. количество строк увеличивается на 1).
Построить область допустимого решения (ОДР) можно также с помощью этого сервиса.

Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.

1. На плоскости X₁0X₂ строят прямые.
2. Определяются полуплоскости.
3. Определяют многоугольник решений;
4. Строят вектор N(c₁,c₂), который указывает направление целевой функции;
5. Передвигают прямую целевую функцию c₁x₂ + c₂x₂ = 0 в направлении вектора N до крайней точки многоугольника решений.
6. Вычисляют координаты точки и значение целевой функции в этой точке.

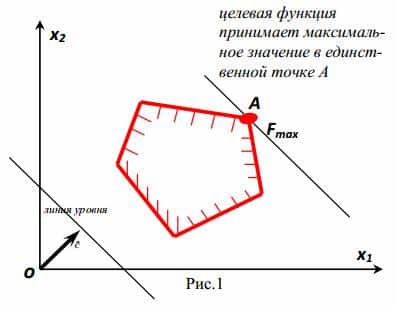
Целевая функция принимает экстремальное (минимальное или максимальное) значение в единственной точке А.

1. Сформулировать математическую модель задачи линейного программирования.
2. Решить задачу линейного программирования графическим способом (для двух переменных).

Если количество переменных в задаче линейного программирования больше двух, то задачу предварительно сводят к стандартной ЗЛП.
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅ → max при ограничениях:
x₁ + x₂ + x₃=12
2x₁ — x₂ + x₄=8
— 2x₁ + 2x₂ + x₅=10
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:

1	1	1	0	0	12
2	-1	0	1	0	8
-2	2	0	0	1	10

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₃.
2. В качестве базовой переменной можно выбрать x₄.
3. В качестве базовой переменной можно выбрать x₅.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x₁ + x₂ + x₃ = 12
2x₁ — x₂ + x₄ = 8
— 2x₁ + 2x₂ + x₅ = 10
Выразим базисные переменные через остальные:
x₃ = — x₁ — x₂+12
x₄ = — 2x₁ + x₂+8
x₅ = 2x₁ — 2x₂+10
Подставим их в целевую функцию:
F(X) = 3x₁ — 2x₂ + 5(- x₁ — x₂+12) — 4(2x₁ — 2x₂+10)
или
F(X) = — 10x₁ + x₂+20 → max
Система неравенств:
— x₁ — x₂+12 ≥ 0
— 2x₁ + x₂+8 ≥ 0
2x₁ — 2x₂+10 ≥ 0
Приводим систему неравенств к следующему виду:
x₁ + x₂ ≤ 12
2x₁ — x₂ ≤ 8
— 2x₁ + 2x₂ ≤ 10
F(X) = — 10x₁ + x₂+20 → max

Особенности решения задач линейного программирования графическим методом

Переменную x₂ принимаем в качестве дополнительной переменной и делаем замену на знак «≥»:
f=x₁ + 6x₃+ 27
x₁ + 3x₃≥6

Далее задача решается графическом способом.

Пример №2
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅ → max при ограничениях:
x₁ + x₂ + x₃=12
2x₁ — x₂ + x₄=8
— 2x₁ + 2x₂ + x₅=10
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:

1	1	1	0	0	12
2	-1	0	1	0	8
-2	2	0	0	1	10

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₃.
2. В качестве базовой переменной можно выбрать x₄.
3. В качестве базовой переменной можно выбрать x₅.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x₁ + x₂ + x₃ = 12
2x₁ — x₂ + x₄ = 8
— 2x₁ + 2x₂ + x₅ = 10
Выразим базисные переменные через остальные:
x₃ = — x₁ — x₂+12
x₄ = — 2x₁ + x₂+8
x₅ = 2x₁ — 2x₂+10
Подставим их в целевую функцию:
F(X) = 3x₁ — 2x₂ + 5(- x₁ — x₂+12) — 4(2x₁ — 2x₂+10)
или
F(X) = — 10x₁ + x₂+20 → max
Система неравенств:
— x₁ — x₂+12 ≥ 0
— 2x₁ + x₂+8 ≥ 0
2x₁ — 2x₂+10 ≥ 0
Приводим систему неравенств к следующему виду:
x₁ + x₂ ≤ 12
2x₁ — x₂ ≤ 8
— 2x₁ + 2x₂ ≤ 10
F(X) = — 10x₁ + x₂+20 → max

• Составить систему математических зависимостей (неравенств) и целевую функцию.
• Изобразить геометрическую интерпретацию задачи.
• Найти оптимальное решение.
• Провести аналитическую проверку.
• Определить существенные и несущественные ресурсы и их избытки.
• Определить значение целевой функции.
• Вычислить объективно обусловленные оценки.
• Составить соотношение устойчивости.

Источник

Вектор-градиент, линия уровня, область допустимых решений в задаче лп. Геометрическая интерпретация задачи линейного программирования.

Множество допустимых решений – это пересечение всех прямых, соответствующих линейным ограничениям типа рав-ва и всех полуплоскостей, соответствующих ограничениям типа нерав-ва.

Для линейной функции градиент – это в-р, состоящий из коэффициентов этой ф-ии. Он показывает направление увеличения ф-ии. Через выбранное решение проводим линию уровня целевой ф-ии. Для линейной ф-ии линия уровня – это прямая, перпендикулярная градиенту.

Геом.интерпретация: область допустимых решений – многогранник в пространстве или многоугольник на плоскости, линии постоянных значений целевой функции. Процесс решения состоит в совмещении линии до конца пересечения с областью допустимых значений при наибольшем значении целевой функции в этой точке пересечения- оптимальное решение ( крайнее положение). Метод-перебор угловых точек.

Многошаговые процессы решений в экономике. Суть метода динамического программирования. Параметр состояния и функция состояния системы, рекуррентные соотношения.

Динамическое программирование представляет собой математический аппарат, разработанный для решения некоторого класса задач математического программирования путем их разложения на относительно небольшие и, следовательно, менее сложные задачи. Специфика метода динамического программирования состоит в том, что для отыскания оптимального управления планируемая операция разделяется на ряд последовательных шагов или этапов. Соответственно и сам процесс планирования операции становится многошаговым и развивается последовательно, от этапа к этапу, причем каждый раз оптимизируется управление только на одном шаге. Динамическое программирование — это планирование дальновидное, с учетом перспективы

Некоторые операции естественно распадаются на этапы, в других это деление приходится вводить искусственно. Примером «естественно многоэтапной» операции может служить планирование работы предприятия на некоторый период времени, состоящий из нескольких хозяйственных лет или кварталов.

Динамическое программирование — это вычислительный метод для решения задач управления определенной структуры, когда задача с переменными представляется как многошаговый процесс принятия решений и на каждом шаге определяется экстремум функции только от одной переменной. n

Знакомство с методом динамического программирования

Процесс динамического программирования разворачивается от конца к началу. Сначала делаются различные предположения о том, чем кончился предпоследний шаг, и для каждого из них выбирается управление на последнем. Затем делаются различные предположения о том, чем кончился предпредпоследний шаг, т. е. рассматриваются различные состояния системы на третьем от конца шаге и выбирается управление на втором от концы шаге так, чтобы оно вместе в уже выбранным управлением на последнем шаге обеспечивало наилучший эффект на двух последних шагах, и так далее, вплоть до первого от начала шага, с которого начинался процесс.

Принцип искать всегда оптимальное продолжение процесса относительно того состояния, которое достигнуто в данный момент, принято называть принципом оптимальности.

Состояние на каждом шаге характ-ся некоторой переменной величиной, кот. называется параметром состояния. Наилучший эффект на данном этапе вместе с уже рассмотренными шагами хар-ся функцией состояния. Решение конкретной задачи методом динамич. программирования сводится к выбору параметра состояния, составлению ф-ии состояния и рекурентных соотношений, связывающих ф-ии состояния для двух соседних последовательных этапов, и их применению для выбора оптимального управления.

Источник