Линейное программирование. Угловые точки допустимых множеств.
при условии, что 
,
,
или 
,
, и
,
,
называется задачей линейного программирования в произвольной форме записи.
Определение 2. Задача в матричной форме вида
(1)
называется симметричной формой записи задачи линейного программирования.
Определение 3. Задача линейного программирования вида
(2)
называется канонической формой записи задачи линейного программирования.
Любую задачу линейного программирования можно привести к канонической форме.
Если система ограничений задана в форме ,
то можно, введя дополнительные переменные, привести ее к виду
, 
,
, где
.
Если же ограничения в задаче заданы в форме , то
, 
,
.
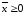
Рассмотрим задачу с ограничениями . Эту систему ограничений можно представить в виде системы
.
Введем следующие обозначения:
,
,…,
,
,…,
,
.
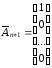
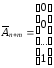
Тогда задачу линейного программирования можно записать в виде:
, 
.
Векторы 
называются векторами условий, а сама задача линейного программирования называется расширенной по отношению к исходной. Пусть
и
— допустимые множества решений исходной и расширенной задач соответственно.
Тогда любой точке множества 
соответствует единственная точка множества
и наоборот. В общем случае, допустимое множество
исходной задачи есть проекция множества
расширенной задачи на подпространство исходных переменных.
Определение 4. Набор чисел , удовлетворяющий ограничениям задачи линейного программирования называется еепланом.
Определение 5. Решением задачи линейного программирования называется ее план, минимизирующий (или максимизирующий) линейную форму.
Введем понятие базисного решения. Из матрицы расширенной задачи 
выберем
линейно независимых векторов-столбцов, которые обозначим как матрицу
, а через
обозначим матрицу из оставшихся столбцов. Тогда
, и ограничения расширенной задачи линейного программирования можно записать в виде:
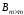
. (3)
Очевидно, что столбцы матрицы 
образуют базис
-мерного пространства. Поэтому вектор
и любой столбец матрицы
можно представить в виде линейной комбинации столбцов матрицы
.
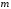
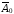
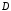
Умножим (3) на слева
, (4)
и найдем отсюда :
. (5)
Придавая 
различные значения, будем получать различные решения
.
Если положить , то
. (6)
Решение (6) называют базисным решением системы из 
уравнений с
неизвестными.
Если полученное решение содержит только положительные компоненты, то оно называется базисным допустимым.
Особенность допустимых базисных решений состоит в том, что они являются крайними точками допустимого множества расширенной задачи.
Если среди компонент нет нулевых, то базисное допустимое решение называетсяневырожденным.
Определение 6. План 
задачи линейного программирования будем называть опорным, если векторы условий
с положительными коэффициентами линейно независимы.
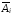
То есть опорный план – это базисное допустимое решение расширенной системы, угловая точка многогранника решений.
Теорема 1: (основная теорема линейного программирования):
- Линейная форма
достигает своего минимума в угловой точке многогранника решений. - Если она принимает минимальное решение более чем в одной угловой точке, то она достигает того же самого значения в любой точке, являющейся выпуклой комбинацией этих угловых точек.
достигает своего минимума в угловой точке многогранника решений.Доказательство: Доказательство теоремы основано на следующей лемме. Лемма: Если 
— замкнутое, ограниченное, выпуклое множество, имеющее конечное число крайних (угловых) точек, то любая точка
может быть представлена в виде выпуклой комбинации крайних точек
. 1) Пусть 
— некоторая внутренняя точка. Многогранник ограниченный замкнутый, имеет конечное число угловых точек.
— допустимое множество. 
Предположим, что точка 
является оптимальной точкой, то есть
,
. Предположим, что точка
не является угловой. Тогда на основании леммы точку
можно выразить через угловые точки многогранника
, т.е. 
, 
,
. Так как функция 
линейна, то 
. (*) Выберем среди точек 
ту, в которой линейная форма
принимает наименьшее значение. Пусть это будет точка
. Обозначим минимальное значение функции в угловой точке через
: 
. Подставим данное значение функции в линейную форму (*) вместо
и получим: 
. Так как 
— оптимальная точка, то получили противоречие:
(!). Следовательно,
,
— угловая точка. 2) Предположим, что линейная форма 
принимает минимальное значение более чем в одной угловой точке, например, в угловых точках
. Тогда если
является выпуклой комбинацией этих точек, то есть 
, 
и
, то 
. То есть, если минимальное значение достигается более чем в одной угловой точке, то того же самого значения линейная форма достигает в любой точке, являющейся выпуклой комбинацией этих угловых точек.
Поиск угловых точек
Для удобства поиска угловых точек в задачу линейного программирования следует приводить к каноническому виду (КЗЛП).
Это задача на максимум 1, для не отрицательных переменных это 3-ка, в этой задаче n-переменных и m-равенств.
Любую ЗЛП можно привести к эквивалентвоной КЗЛП (решения которых одинаковые)
Дополнительные неотрицательные переменные X’ и X** называются слековыми (X*) переменными и сурклассовые (X**) переменные. Они имеют простой экономический смысл, пусть ограничение по ресурсам 10 – это запасы ресурсов, тогда Х* слековое, остаток от запаса ресурса 10. Если затраты этих ресурсов 3X1-4X2+5X3/.
Если ресурс расходуется полностью то сллековое X’ расходуется полностью, в угловых точках одна или все слековые переменные могут быть нулевые. Если 3 это минимальный уровень для какого-то параметра, то сурплассовые переменные Х”, это превосходство параметра 7Х1+5Х2+6Х3 над тройкой.
В угловой точке сурплассовые переменные так же может быть нулевой.
Для экономики этого достаточно, чтобы получить эквивалентное КЗЛП, но в произвольных задачах необходимо и третье преобразование.
X 0 От такой переменной легко перейти к неотрицательной переменной. Если вспомнить 4-ый класс школы))) x=x’-x”, x’,x”=>0 Любое число можно представить в виде разности двух неотрицательных чисел и подставить это в ЗЛП.
Пример приведения к канонического виду.
Получив КЗЛП нам надо научиться решать только КЗЛП.
После преобразования любой КЗЛП к канонической всегда получим, что число неизвестный n>m, то есть система уравнений для неотрицательных переменных имеет степень свободы n-m=5-3=2.
Поиск решения системы для которой n>m.
Для решения такой системы необходимо задать n-m переменных, которые называются небазисными, независимыми, сободными, а остальные M ПЕРЕМЕННЫХ получить из решения системы эти переменные называются базисными (зависимыми, не свободными). Пусть…
Если взять в качестве небазисных X1=2 и X2=3, отсюда получаем базисные Х3=30-6*2-5*3=3, Х4=6-2-6=-2, Х5=4. Точка с координатами 2 и 3 недопустима, так как второй ресурса не хватает (слековая переменная отрицательна). Для поиска угловой точки, следует воспользоваться следующим свойством (теорема об алгебраическом характере угловой точки).
Пусть есть КЗЛП n>m, тогда решение системы Ах=b дает угловую точку, тогда и только тогда, когда оно опорное. Решение называется опорным, если оно не отрицательное (допустимое и базисное).
Решение называется базисным, если небазисные переменные в количестве n-m=0.
Для любой системы число базисных решений конечное
….*** НАЙДЕМ БАЗИСНОЕ, ВЫБЕРЕМ ОПОРНОЕ,А ИЗ ОПОРНЫХ ОПТИМАЛЬНОЕ
Составим все возможные комбинации…
Аналогичным образом можно получить все 10 базисных решений и выбрать из них 5 угловых точек, а именно
Точка К для канонической задачи, является оптимальной точкой (аналогично на графике), для неё Х1=0, Х2=3. Слековые переменные Х3=15, Х4=0, а сурклассовая Х5=2. При этом небазисная переменная (образующая угловую точку) Х4=0 и Х1=0, т.е. выпускается только второй продукт в количестве трех единиц, при этом первый ресурс в избытке 15 единиц, второй ресурс истрачены все 6 единиц,а превышение над уровнем единицы составляет двойка.
Если есть задача каноническая и у неё есть оптимальное решение, то у этой задачи, обязательно найдется оптимальная точка – угловая, когда не нулевых переменных будет не больше n, т.е. если в задачи экономики и управления есть m ограничений любого вида , а неизвестных m продуктов которых нужно выпустить,то из n продуктов выпускаться в оптимальном плане будет выпускаться не больше m.
Пусть предприятие выпускает 15 продуктов, используя 4 ресурса, тогда из 15-ти следует выпускать не больше 4-ех.
Или в транспортной задачи, пусть у Вас 10 поставщиков и 20-ть потребителей (всего путей 200),в оптимальном плане будет задействовано не больше, чем (10+20-1) 29 путей.
Теорема о алгебраической характеристики угловой точки позволяет заранее сказать о числе нулей в решении, то есть о количестве рентабельных и не рентабельных продуктов.
Метод перебора угловых точек.
- Из канонических соображений убеждаемся что задача имеет оптимальное решение, чтобы не попасть в ситуацию III.
- Приводим к задачам КЗЛП.
- Ищем все базисные решения Сn m
- Из них выбираем неотрицательные – опорные угловые.
- Из угловых выбираем наилучшую по функции цели.
Задача по варианту, показать область допустимых значений, написать координат угловой точки.