Удаление элемента бинарного дерева java

Структуры данных: двоичное дерево в Java

Привет-привет! Сложно быть сильным программистом без базовых знаний. И здесь имеется в виду не только знание синтаксиса родного языка программирования, но и основ и концепций программирования в целом. Одними из таких основ являются алгоритмы и структуры данных. Как правило в данном вопросе кто-то осведомлен больше, кто-то меньше, но есть некоторая база, которую должны знать все. Среди баз для структур данных обязательно стоит разобраться с деревьями двоичного поиска. Собственно, сегодня мы рассмотрим саму структуру с её особенностями и узнаем, как можно реализовать двоичное дерево в Java . Для начала давайте же разберемся, что такое двоичное дерево. Двоичное де́рево — структура данных, в которой каждый узел (родительский) имеет не более двух потомков (правый и левый наследник).На практике обычно используются два вида двоичных деревьев — двоичное дерево поиска и пирамида (куча). Сегодня мы рассмотрим двоичное дерево поиска.

Преимущества двоичного дерева

1. Делим справочник на две части, первая — от 1 до 50, вторая 51-100. Мы точно знаем, в которой из этих частей наша страница: если опять же брать 77 страницу — во второй части книги.
2. Далее рассматриваем вторую часть и делим её на две — от 51 до 75, от 76 до 100. В этом случае наша страница будет опять во второй половине, в промежутке 76-100.
3. Далее делим и этот промежуток на 2 и получаем 76-88 и 89-100. Страница входит в первый промежуток, поэтому второй отметаем.
4. Далее промежутки: 76-81 и 82-88, берем первый.
5. 76-78 и 79-81, берем первый.
6. 76 и 77-78, берем второй.
7. 77 и 78, берем первый и получаем нашу страницу — 77.

Правила построения дерева двоичного поиска

Двоичное дерево поиска строится по определенным правилам:

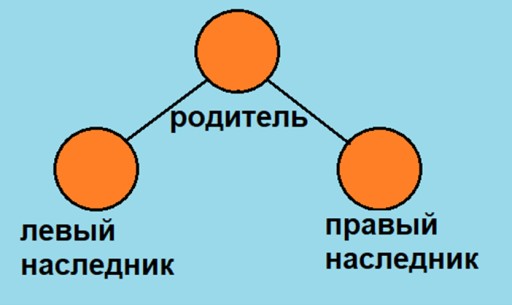
• каждый узел имеет не более двух детей;
• каждое значение, меньшее, чем значение узла, становится левым ребенком или ребенком левого ребенка;
• каждое значение, большее или равное значению узла, становится правым ребенком или ребенком правого ребенка.

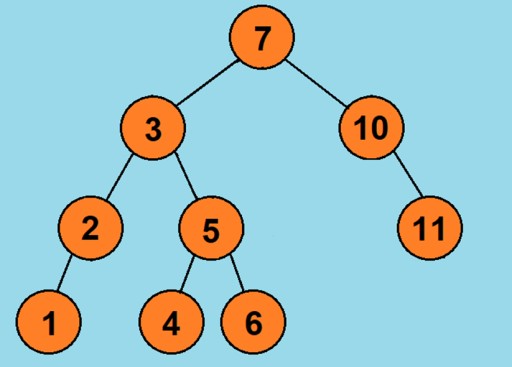
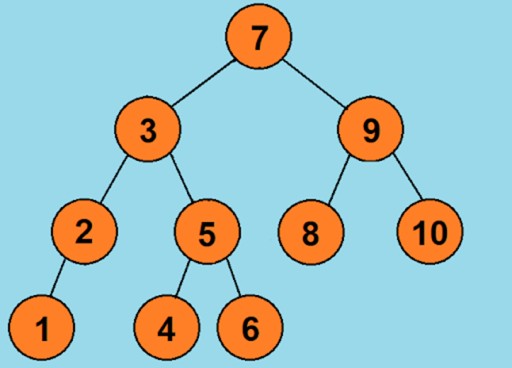
К примеру, у нас есть ряд из чисел от 1 до 10. Давайте посмотрим, как будет выглядеть дерево двоичного поиска для этого ряда:Давайте подумаем, соблюдаются ли тут все условия бинарного дерева:

• все узлы имеют не более двух наследников, первое условие соблюдается;
• если мы рассмотрим к примеру узел со значением 7(или любой другой), то увидим что все значения элементов в левом поддереве будут меньше, в правом — больше. А это значит, что условия 2 и 3 соблюдены.

Разберем, каким образом происходят основные операции — вставка, удаление, поиск.

Поиск элемента

При поиске элемента с заданным значением мы начинаем с корневого элемента:

1. Если он равен искомому значению, корневой элемент и есть искомый, если нет — сравниваем значения корневого и искомого.
2. Если искомый элемент больше, мы переходим к правому потомку, если нет — к левому.
3. Если элемент не найден, применяем шаги 1 и 2, но уже к потомку (правому или левому) до тех пор, пока элемент не будет найден.

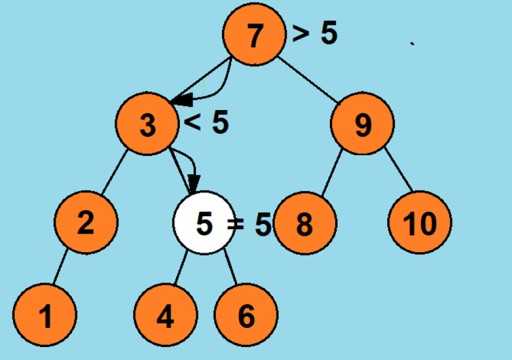
К примеру, в продемонстрированном выше дереве двоичного поиска мы хотим найти элемент со значением 5:

• сравниваем его с корневым элементом, видим, что корневой больше, поэтому мы переходим к левому потомку, который имеет значение 3;
• сравниваем искомый и элемент со значением 3, видим, что искомый больше, поэтому нам нужен правый потомок рассматриваемого элемента, а именно — элемент со значением 5;
• сравниваем этого потомка с искомым и видим, что значения равны — элемент найден.

Вставка элемента

1. Сравниваем новый с корневым (если его нет — новый элемент и есть корневой).
2. Если новый элемент:
   • меньше, то переходим к левому наследнику, если его нет, новый элемент и занимает место левого наследника, и алгоритм закончен;
   • больше или равен корневому, то мы переходим к правому наследнику. И аналогично, если данного элемента нет, то новый элемент займет место правого элемента и алгоритм закончен.

• сравниваем с корневым элементом 7 и видим, что корневой меньше, поэтому переходим к правому наследнику;
• следующий рассматриваемый элемент имеет значение 9, что меньше чем новый 11, поэтому переходим к правому наследнику;
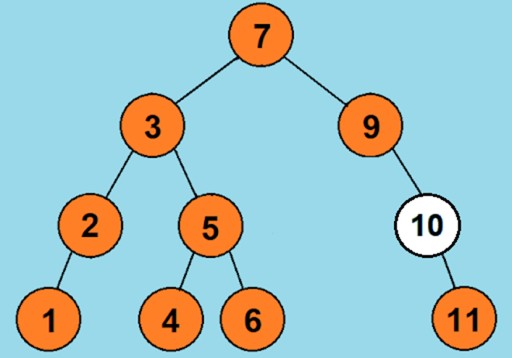
• правый наследник имеет значение 10, что опять же меньше, поэтому мы переходим к первому элементу, а так как его нет, то новый элемент со значением 11 и становится на это место.

↓

Удаление элемента

Пожалуй, из всех операций с деревьями двоичного поиска, удаление — наиболее сложная. В первую очередь происходит поиск удаляемого элемента, после нахождения которого следует этап, у которого могут быть три вариации:

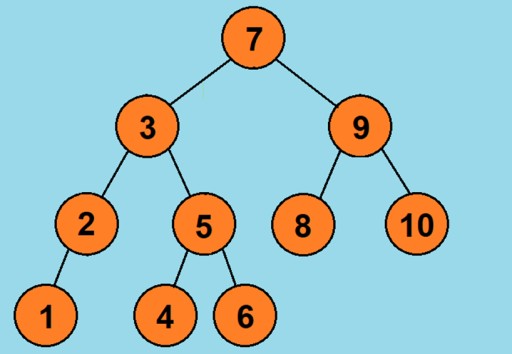
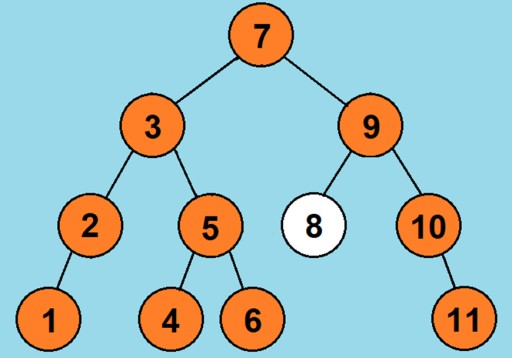
1. Удаляемый узел является листовым (не имеет потомков). Пожалуй, самый простой. Всё сводится к тому, что мы его просто отсекаем от дерева, без лишних манипуляций. К примеру, из нашего дерева мы удаляем узел со значением 8: ↓
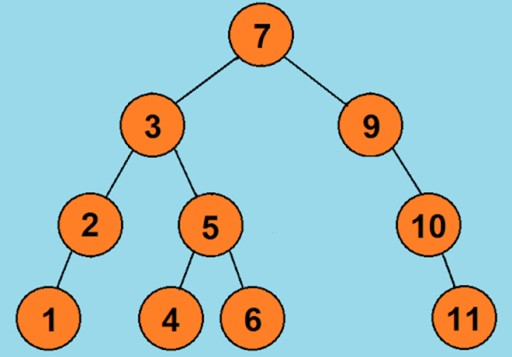
2. Удаляемый узел имеет одного потомка. В таком случае мы удаляем выбранный узел, и на его место ставим его потомка (по сути просто вырежем выбранный узел из цепочки). В качестве примера удалим из дерева узел со значением 9: ↓
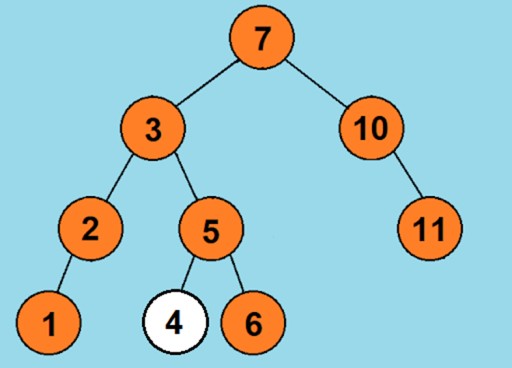
3. Удаляемый узел имеет двух потомков. Самая интересная часть. Ведь если удаляемый узел имеет сразу двух потомков, нельзя просто так заменить его одним из этих потомков (особенно если у потомка есть собственные потомки). Пример: в рассматриваемом выше дереве, какой узел должен быть левым потомком узла 3? Если немного задуматься, то станет очевидно, что это должен быть узел со значением 4. Ну а если дерево не будет таким простым? Если оно будет вмещать сотни значений, будет ли так просто понять, кто будет преемником? Понятное дело, что нет. Поэтому тут нужен свой небольшой алгоритм поиска приемника:
   1. Сперва мы должны перейти к правому потомку выбранного узла, значение которого должно быть больше значения узла.
   2. После мы переходим к левому потомку правого потомка (если такой существует), дальше — к левому потомку левого потомка и т. д., следуя вниз по цепи левых потомков.
   3. Соответственно, последний левый потомок на этом пути и будет являться преемником исходного узла.

   Давайте немного обобщим этот небольшой алгоритм: в поддереве правого потомка исходного узла все узлы больше удаляемого, что можно понять из основных правил дерева двоичного поиска. В этом поддереве мы и ищем наименьшее значение.

   Иными словами, мы ищем наименьший узел в наборе узлов, больших исходного узла. Этот наименьший узел среди больших и будет наиболее подходящим преемником.

   Как будет выглядеть дерево после удаления узла со значением 3:

   

   ↓

А теперь пришло время перейти от практики к теории. Давайте взглянем, каким же образом можно отобразить данную структуру данных в Java. Класс одного узла:

 class Node < private int value; // ключ узла private Node leftChild; // Левый узел потомок private Node rightChild; // Правый узел потомок public void printNode() < // Вывод значения узла в консоль System.out.println(" Выбранный узел имеет значение :" + value); >public int getValue() < return this.value; >public void setValue(final int value) < this.value = value; >public Node getLeftChild() < return this.leftChild; >public void setLeftChild(final Node leftChild) < this.leftChild = leftChild; >public Node getRightChild() < return this.rightChild; >public void setRightChild(final Node rightChild) < this.rightChild = rightChild; >@Override public String toString() < return "Node class Tree < private Node rootNode; // корневой узел public Tree() < // Пустое дерево rootNode = null; >public Node findNodeByValue(int value) < // поиск узла по значению Node currentNode = rootNode; // начинаем поиск с корневого узла while (currentNode.getValue() != value) < // поиск покуда не будет найден элемент или не будут перебраны все if (value < currentNode.getValue()) < // движение влево? currentNode = currentNode.getLeftChild(); >else < //движение вправо currentNode = currentNode.getRightChild(); >if (currentNode == null) < // если потомка нет, return null; // возвращаем null >> return currentNode; // возвращаем найденный элемент > public void insertNode(int value) < // метод вставки нового элемента Node newNode = new Node(); // создание нового узла newNode.setValue(value); // вставка данных if (rootNode == null) < // если корневой узел не существует rootNode = newNode;// то новый элемент и есть корневой узел >else < // корневой узел занят Node currentNode = rootNode; // начинаем с корневого узла Node parentNode; while (true) // мы имеем внутренний выход из цикла < parentNode = currentNode; if(value == currentNode.getValue()) < // если такой элемент в дереве уже есть, не сохраняем его return; // просто выходим из метода >else if (value < currentNode.getValue()) < // движение влево? currentNode = currentNode.getLeftChild(); if (currentNode == null)< // если был достигнут конец цепочки, parentNode.setLeftChild(newNode); // то вставить слева и выйти из методы return; >> else < // Или направо? currentNode = currentNode.getRightChild(); if (currentNode == null) < // если был достигнут конец цепочки, parentNode.setRightChild(newNode); //то вставить справа return; // и выйти >> > > > public boolean deleteNode(int value) // Удаление узла с заданным ключом < Node currentNode = rootNode; Node parentNode = rootNode; boolean isLeftChild = true; while (currentNode.getValue() != value) < // начинаем поиск узла parentNode = currentNode; if (value < currentNode.getValue()) < // Определяем, нужно ли движение влево? isLeftChild = true; currentNode = currentNode.getLeftChild(); >else < // или движение вправо? isLeftChild = false; currentNode = currentNode.getRightChild(); >if (currentNode == null) return false; // yзел не найден > if (currentNode.getLeftChild() == null && currentNode.getRightChild() == null) < // узел просто удаляется, если не имеет потомков if (currentNode == rootNode) // если узел - корень, то дерево очищается rootNode = null; else if (isLeftChild) parentNode.setLeftChild(null); // если нет - узел отсоединяется, от родителя else parentNode.setRightChild(null); >else if (currentNode.getRightChild() == null) < // узел заменяется левым поддеревом, если правого потомка нет if (currentNode == rootNode) rootNode = currentNode.getLeftChild(); else if (isLeftChild) parentNode.setLeftChild(currentNode.getLeftChild()); else parentNode.setRightChild(currentNode.getLeftChild()); >else if (currentNode.getLeftChild() == null) < // узел заменяется правым поддеревом, если левого потомка нет if (currentNode == rootNode) rootNode = currentNode.getRightChild(); else if (isLeftChild) parentNode.setLeftChild(currentNode.getRightChild()); else parentNode.setRightChild(currentNode.getRightChild()); >else < // если есть два потомка, узел заменяется преемником Node heir = receiveHeir(currentNode);// поиск преемника для удаляемого узла if (currentNode == rootNode) rootNode = heir; else if (isLeftChild) parentNode.setLeftChild(heir); else parentNode.setRightChild(heir); >return true; // элемент успешно удалён > // метод возвращает узел со следующим значением после передаваемого аргументом. // для этого он сначала переходим к правому потомку, а затем // отслеживаем цепочку левых потомков этого узла. private Node receiveHeir(Node node) < Node parentNode = node; Node heirNode = node; Node currentNode = node.getRightChild(); // Переход к правому потомку while (currentNode != null) // Пока остаются левые потомки < parentNode = heirNode;// потомка задаём как текущий узел heirNode = currentNode; currentNode = currentNode.getLeftChild(); // переход к левому потомку >// Если преемник не является if (heirNode != node.getRightChild()) // правым потомком, < // создать связи между узлами parentNode.setLeftChild(heirNode.getRightChild()); heirNode.setRightChild(node.getRightChild()); >return heirNode;// возвращаем приемника > public void printTree() < // метод для вывода дерева в консоль Stack globalStack = new Stack(); // общий стек для значений дерева globalStack.push(rootNode); int gaps = 32; // начальное значение расстояния между элементами boolean isRowEmpty = false; String separator = "-----------------------------------------------------------------"; System.out.println(separator);// черта для указания начала нового дерева while (isRowEmpty == false) < Stack localStack = new Stack(); // локальный стек для задания потомков элемента isRowEmpty = true; for (int j = 0; j < gaps; j++) System.out.print(' '); while (globalStack.isEmpty() == false) < // покуда в общем стеке есть элементы Node temp = (Node) globalStack.pop(); // берем следующий, при этом удаляя его из стека if (temp != null) < System.out.print(temp.getValue()); // выводим его значение в консоли localStack.push(temp.getLeftChild()); // соохраняем в локальный стек, наследники текущего элемента localStack.push(temp.getRightChild()); if (temp.getLeftChild() != null || temp.getRightChild() != null) isRowEmpty = false; >else < System.out.print("__");// - если элемент пустой localStack.push(null); localStack.push(null); >for (int j = 0; j < gaps * 2 - 2; j++) System.out.print(' '); >System.out.println(); gaps /= 2;// при переходе на следующий уровень расстояние между элементами каждый раз уменьшается while (localStack.isEmpty() == false) globalStack.push(localStack.pop()); // перемещаем все элементы из локального стека в глобальный > System.out.println(separator);// подводим черту > > 

Опять же, ничего особо сложного. Присутствуют операции для дерева двоичного поиска, описанные ранее, плюс метод для отображения дерева в консоли. Ну а теперь взглянем на дерево в действии:

Операции поиска/вставки/удаления в дереве двоичного поиска имеют временную сложность O(log(N)) . Но это в лучшем случае. Вообще, временная сложность операций варьируется от O(log(N)) до O(N) . Это зависит от степени вырожденности дерева.

Что такое вырожденное дерево?

Это дерево, в котором элементы попадали при добавлении в позицию крайнего левого узла (наименьшие число) или крайнего большего узла (наибольшие). Это может случиться, если, например, всё левое дерево пусто на каждом уровне, есть только правые деревья, и в таком случае дерево вырождается в список (идущий вправо). Да, именно так вырожденное дерево фактически становится односвязным списком, в котором каждый элемент знает только о последующем за ним. В таком случае все операции по данной структуре приближаются ко временной сложности O(N) .

В каком случае дерево может стать вырожденным?

Например, если добавлять список отсортированных элементов. Если список отсортирован по возрастанию, то корнем будет первый, соответственно, наименьший. Следующий после него займет позицию правого потомка. А тот, который попадет после, будет больше второго и займет позицию его правого преемника, и так далее… Если же список будет по убыванию, то будет то же самое, но уже с крайними левыми элементами. Чтобы избежать этого, можно после получения ряда элементов попросту их перемешать. Тогда сортированность пропадет, и числа будет более-менее равномерно разбросаны по дереву. На этом у меня сегодня всё, спасибо за уделенное внимание!

Источник

Delete or remove node from binary search tree (BST) – (Java/ DFS/ Example)

Examples – delete a node from binary search tree (bst) using java

Fig 1: Delete nodes of BST

Example 1: Delete leaf node E from BST using java

• Delete the Node from binary tree having value 75 (Node E).
• Search or find a node in BST
  • node.data == 75

  Example 2: Remove Node having one child from BST in java

  • We would like to delete Node B from BST.
  • Node B is child node so we can not directly remove the node B.
  • We will follow the below procedure to delete the node B.

  Fig 3: Delete Non Leaf node B

  • Search the node (Node B) in BST to be deleted
    • node.data == inputNumber
    • Connect Node A to Node D.
    • Link of Node B is removed from BST

    Example 3: Delete node having left & right child nodes from BST

    Let us delete Node C from binary search tree.

    • Node C has left and right child, so we can not delete the Node C from binary search tree
      • Otherwise we will lose underlying nodes.

      Algorithm: remove node having both child nodes from BST using java

      

      Fig 4: Delete non leaf node C

      • Search the Node C in BST
      • Check Node C is non leaf node
      • Non Leaf node has both left and right child nodes.
        • We need to reduce this case to either example 1 or example 2
        • We can not delete Node C directly.
        • We found Node J (data is 160) in right subtree
        • Node C will have value equals 160.
        • We have reduced it to Example 1 (deleting a leaf node)

        Program – delete or remove node from binary search tree (BST) using java

        We have categorized the code into three sections [Example 1, Example 3 and Example 3], as discussed above.

        1.) DeleteNodeInBST Class:

        • DeleteNodeInBST delete the node from BST and DeleteNodeInBST has following methods:
          1. min method, finds the minimum element in the right subtree.
          2. deleteNodeInBST method, delete a node from binary search tree.
          3. inorder method will print the binary tree in sorted order.

        package org.learn.Question; import org.learn.PrepareTree.Node; public class DeleteNodeInBST < public static void inorder(Node root) < if (root == null) return; inorder(root.left); System.out.printf("%d ", root.data); inorder(root.right); >private static int min(Node node) < if (node.left == null) < return node.data; >return min(node.left); > public static Node deleteNodeInBST(Node node, int data) < if (null == node) < System.out.println("Element is not there in binary search tree"); return null; >if (data < node.data) < node.left = deleteNodeInBST(node.left, data); >else if (data > node.data) < node.right = deleteNodeInBST(node.right, data); >else < // case for equality // Now we see that whether we can directly delete the node // [Scenario 3] if (node.left != null && node.right != null) < int minInRightSubTree = min(node.right); node.data = minInRightSubTree; node.right = deleteNodeInBST(node.right, minInRightSubTree); >else < // either one child or leaf node // [Scenario 1 and Scenario 2] if (node.left == null && node.right == null) < node = null; >else > > return node; > >

        2.) Node Class:

        package org.learn.PrepareTree; public class Node < public int data; public Node left; public Node right; public Node(int num) < this.data = num; this.left = null; this.right = null; >public Node() < this.left = null; this.right = null; >public static Node createNode(int number) < return new Node(number); >>

        3.) App Class:

        • We are creating the binary tree in main method.
        • We are deleting a node from binary search tree.
        • We are printing the BST using InOrder binary tree traversal.

        package org.learn.Client; import org.learn.PrepareTree.Node; import org.learn.Question.DeleteNodeInBST; public class App < public static void main( String[] args ) < //root level 0 Node A = Node.createNode(100); //Level 1 Node B = Node.createNode(50); Node C = Node.createNode(150); //Level 2 Node D = Node.createNode(25); Node E = Node.createNode(75); Node F = Node.createNode(125); Node G = Node.createNode(175); //Level 3 Node H = Node.createNode(120); Node I = Node.createNode(140); Node J = Node.createNode(160); Node K = Node.createNode(190); //connect Level 0 and 1 A.left = B; A.right = C; //connect level 1 and level 2 B.left = D; B.right = E; C.left = F; C.right = G; //Connect level 2 and level 3 F.left = H; F.right = I; G.left = J; G.right = K; System.out.printf("Deleting %d from binary search tree\n",H.data); DeleteNodeInBST.deleteNodeInBST(A, H.data); System.out.println("Binary Tree after deleting node"); DeleteNodeInBST.inorder(A); System.out.printf("\n\nDeleting %d from binary search tree\n",E.data); DeleteNodeInBST.deleteNodeInBST(A, E.data); System.out.println("Binary Tree after deleting node"); DeleteNodeInBST.inorder(A); System.out.printf("\n\nDeleting %d from binary search tree\n",F.data); DeleteNodeInBST.deleteNodeInBST(A, F.data); System.out.println("Binary Tree after deleting node"); DeleteNodeInBST.inorder(A); System.out.printf("\n\nDeleting %d from binary search tree\n",C.data); DeleteNodeInBST.deleteNodeInBST(A, C.data); System.out.println("Binary Tree after deleting node"); DeleteNodeInBST.inorder(A); >>

        Output – delete or remove node from binary search tree (BST) using java

        Deleting 120 from binary search tree Binary Tree after deleting node 25 50 75 100 125 140 150 160 175 190 Deleting 75 from binary search tree Binary Tree after deleting node 25 50 100 125 140 150 160 175 190 Deleting 125 from binary search tree Binary Tree after deleting node 25 50 100 140 150 160 175 190 Deleting 150 from binary search tree Binary Tree after deleting node 25 50 100 140 160 175 190

        Источник