Tukey hsd test python

ANOVA + Tukey Test In Python

Using Statistical Testing Methods In Python To Develop An Online Advertising Strategy (With Code).

Scenario

Our client is a startup clothing company that specializes in “athleisure” clothing in the US. Their marketing team wants to launch an ad campaign to increase online traffic on its website, which hopefully leads to more revenue. To best allocate time and effort for the launch of the ad campaign and maximize the audience to see their ads, they want to understand 3 things.

Which keywords related to athleisure are consumers searching for most?

Which month are consumers searching for athleisure clothing most?

Which platform are consumers using most for their searches?

Goal

Provide recommendations to the athleisure startup company to determine the best keywords, best timing, and best platform to run their ads.

Data

To collect data for this case study, we will use Wordtracker — a paid database service for Search Engine Optimization (SEO). Search Engine Optimization is essentially just another way of saying:

“I want to figure out how to make my website the top result for a given search.”

Wordtracker helps clients to get more traffic to their website or better understand what consumers are searching for. Wordtracker is similar to Google Keywords Planner service but allows access to search data on platforms beyond Google. At the time the data was extracted, Wordtracker offered a 1-year representative sample of search data from June 2018-May 2019 on Google, Youtube, Amazon, and eBay. It offered over 2 billion unique keywords from 18 million global panelists, across 106 countries. Below is a synopsis of all data in the Wordtracker database related to search volume in the United States.

But how do we decide on which terms related to “athleisure” to select for our search volume queries on Wordtracker? There are many methods, but what better way than to shop for athleisure buzzwords online? We can search the term “athleisure” on Amazon, and…

Источник

Как выполнить тест Тьюки в Python

Однофакторный дисперсионный анализ используется для определения того, существует ли статистически значимое различие между средними значениями трех или более независимых групп.

Если общее значение p из таблицы ANOVA меньше некоторого уровня значимости, то у нас есть достаточно доказательств, чтобы сказать, что по крайней мере одно из средних значений групп отличается от других.

Однако это не говорит нам, какие группы отличаются друг от друга. Это просто говорит нам, что не все средние группы равны. Чтобы выяснить, какие именно группы отличаются друг от друга, мы должны провестиапостериорный тест .

Одним из наиболее часто используемых апостериорных тестов является тест Тьюки , который позволяет нам проводить попарные сравнения между средними значениями каждой группы, при этом контролируя частоту ошибок по семействам .

В этом руководстве представлен пошаговый пример выполнения теста Тьюки в Python.

Шаг 1: Загрузите необходимые пакеты и функции

Во-первых, мы загрузим необходимые пакеты и функции в Python:

import pandas as pd import numpy as np from scipy. stats import f_oneway from statsmodels. stats.multicomp import pairwise_tukeyhsd 

Шаг 2: Соответствуйте модели ANOVA

В следующем коде показано, как создать поддельный набор данных с тремя группами (A, B и C) и подогнать к данным однофакторную модель ANOVA, чтобы определить, равны ли средние значения для каждой группы:

#enter data for three groups a = [85, 86, 88, 75, 78, 94, 98, 79, 71, 80] b = [91, 92, 93, 90, 97, 94, 82, 88, 95, 96] c = [79, 78, 88, 94, 92, 85, 83, 85, 82, 81] #perform one-way ANOVA f_oneway(a, b, c) F_onewayResult(statistic=5.167774552944481, pvalue=0.012582197136592609) 

Мы видим, что общее значение p из таблицы ANOVA составляет 0,01258 .

Поскольку это меньше 0,05, у нас есть достаточно доказательств, чтобы сказать, что средние значения по каждой группе не равны.

Таким образом, мы можем приступить к выполнению теста Тьюки, чтобы точно определить, какие средние значения групп различаются.

Шаг 3: Проведите тест Тьюки

Чтобы выполнить тест Тьюки в Python, мы можем использовать функцию pairwise_tukeyhsd () из библиотеки statsmodels :

#create DataFrame to hold data df = pd.DataFrame() # perform Tukey's test tukey = pairwise_tukeyhsd(endog=df['score'], groups=df['group'], alpha= 0.05 ) #display results print(tukey) Multiple Comparison of Means - Tukey HSD, FWER=0.05 ===================================================== group1 group2 meandiff p-adj lower upper reject ----------------------------------------------------- a b 8.4 0.0158 1.4272 15.3728 True a c 1.3 0.8864 -5.6728 8.2728 False b c -7.1 0.0453 -14.0728 -0.1272 True ----------------------------------------------------- 

Вот как интерпретировать вывод:

• P-значение для разницы в средних значениях между a и b: 0,0158 .
• P-значение для разницы в средних значениях между a и c: 0,8864 .
• P-значение для разницы средних значений между b и c: 0,0453 .

Таким образом, мы можем заключить, что существует статистически значимая разница между средними значениями групп а и b и групп b и c , но нет статистически значимой разницы между средними значениями групп а и с .

Источник

scipy.stats.tukey_hsd#

Perform Tukey’s HSD test for equality of means over multiple treatments.

Tukey’s honestly significant difference (HSD) test performs pairwise comparison of means for a set of samples. Whereas ANOVA (e.g. f_oneway ) assesses whether the true means underlying each sample are identical, Tukey’s HSD is a post hoc test used to compare the mean of each sample to the mean of each other sample.

The null hypothesis is that the distributions underlying the samples all have the same mean. The test statistic, which is computed for every possible pairing of samples, is simply the difference between the sample means. For each pair, the p-value is the probability under the null hypothesis (and other assumptions; see notes) of observing such an extreme value of the statistic, considering that many pairwise comparisons are being performed. Confidence intervals for the difference between each pair of means are also available.

Parameters : sample1, sample2, … array_like

The sample measurements for each group. There must be at least two arguments.

Returns : result TukeyHSDResult instance

The return value is an object with the following attributes:

The computed statistic of the test for each comparison. The element at index (i, j) is the statistic for the comparison between groups i and j .

The computed p-value of the test for each comparison. The element at index (i, j) is the p-value for the comparison between groups i and j .

The object has the following methods:

Compute the confidence interval for the specified confidence level.

performs comparison of means against a control group.

The use of this test relies on several assumptions.

1. The observations are independent within and among groups.
2. The observations within each group are normally distributed.
3. The distributions from which the samples are drawn have the same finite variance.

The original formulation of the test was for samples of equal size [6]. In case of unequal sample sizes, the test uses the Tukey-Kramer method [4].

NIST/SEMATECH e-Handbook of Statistical Methods, “7.4.7.1. Tukey’s Method.” https://www.itl.nist.gov/div898/handbook/prc/section4/prc471.htm, 28 November 2020.

Abdi, Herve & Williams, Lynne. (2021). “Tukey’s Honestly Significant Difference (HSD) Test.” https://personal.utdallas.edu/~herve/abdi-HSD2010-pretty.pdf

“One-Way ANOVA Using SAS PROC ANOVA & PROC GLM.” SAS Tutorials, 2007, www.stattutorials.com/SAS/TUTORIAL-PROC-GLM.htm.

Kramer, Clyde Young. “Extension of Multiple Range Tests to Group Means with Unequal Numbers of Replications.” Biometrics, vol. 12, no. 3, 1956, pp. 307-310. JSTOR, www.jstor.org/stable/3001469. Accessed 25 May 2021.

NIST/SEMATECH e-Handbook of Statistical Methods, “7.4.3.3. The ANOVA table and tests of hypotheses about means” https://www.itl.nist.gov/div898/handbook/prc/section4/prc433.htm, 2 June 2021.

Tukey, John W. “Comparing Individual Means in the Analysis of Variance.” Biometrics, vol. 5, no. 2, 1949, pp. 99-114. JSTOR, www.jstor.org/stable/3001913. Accessed 14 June 2021.

Here are some data comparing the time to relief of three brands of headache medicine, reported in minutes. Data adapted from [3].

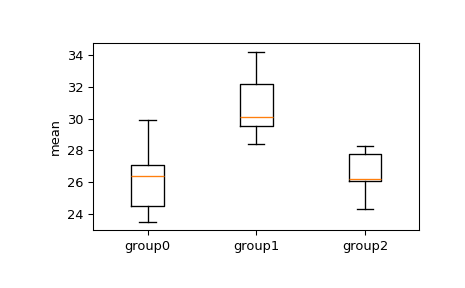
>>> import numpy as np >>> from scipy.stats import tukey_hsd >>> group0 = [24.5, 23.5, 26.4, 27.1, 29.9] >>> group1 = [28.4, 34.2, 29.5, 32.2, 30.1] >>> group2 = [26.1, 28.3, 24.3, 26.2, 27.8] 

We would like to see if the means between any of the groups are significantly different. First, visually examine a box and whisker plot.

>>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots(1, 1) >>> ax.boxplot([group0, group1, group2]) >>> ax.set_xticklabels(["group0", "group1", "group2"]) >>> ax.set_ylabel("mean") >>> plt.show() 

From the box and whisker plot, we can see overlap in the interquartile ranges group 1 to group 2 and group 3, but we can apply the tukey_hsd test to determine if the difference between means is significant. We set a significance level of .05 to reject the null hypothesis.

>>> res = tukey_hsd(group0, group1, group2) >>> print(res) Tukey's HSD Pairwise Group Comparisons (95.0% Confidence Interval) Comparison Statistic p-value Lower CI Upper CI (0 - 1) -4.600 0.014 -8.249 -0.951 (0 - 2) -0.260 0.980 -3.909 3.389 (1 - 0) 4.600 0.014 0.951 8.249 (1 - 2) 4.340 0.020 0.691 7.989 (2 - 0) 0.260 0.980 -3.389 3.909 (2 - 1) -4.340 0.020 -7.989 -0.691 

The null hypothesis is that each group has the same mean. The p-value for comparisons between group0 and group1 as well as group1 and group2 do not exceed .05, so we reject the null hypothesis that they have the same means. The p-value of the comparison between group0 and group2 exceeds .05, so we accept the null hypothesis that there is not a significant difference between their means.

We can also compute the confidence interval associated with our chosen confidence level.

>>> group0 = [24.5, 23.5, 26.4, 27.1, 29.9] >>> group1 = [28.4, 34.2, 29.5, 32.2, 30.1] >>> group2 = [26.1, 28.3, 24.3, 26.2, 27.8] >>> result = tukey_hsd(group0, group1, group2) >>> conf = res.confidence_interval(confidence_level=.99) >>> for ((i, j), l) in np.ndenumerate(conf.low): . # filter out self comparisons . if i != j: . h = conf.high[i,j] . print(f"(i> - j>) l:>6.3f> h:>6.3f>") (0 - 1) -9.480 0.280 (0 - 2) -5.140 4.620 (1 - 0) -0.280 9.480 (1 - 2) -0.540 9.220 (2 - 0) -4.620 5.140 (2 - 1) -9.220 0.540 

Источник