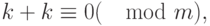Целые переменные в программировании

Содержание

Типы переменных. Целые и вещественные переменные, представление целых и вещественных чисел в компьютере
Типы переменных
Целочисленные переменные

Типы переменных. Целые и вещественные переменные, представление целых и вещественных чисел в компьютере

Аннотация: Определяется понятие типа переменной как множества значений, которые она может принимать, и набора операций, которые можно совершать со значениями. Рассматриваются наиболее важные базовые типы алгоритмического языка — целые и вещественные числа. Подчеркивается особенность представления целых чисел в компьютере как элементов кольца вычетов, рассматривается интерпретация элементов кольца вычетов как неотрицательных чисел или чисел со знаком. Приводится представление вещественных чисел в компьютере в плавающей форме, рассматриваются особенности арифметики плавающих чисел.

Типы переменных

Тип переменной определяется множеством значений, которое она может принимать. Кроме того, тип определяет операции , которые возможны с переменной. Например, с численными переменными возможны арифметические операции , с логическими — проверка, истинно или ложно значение переменной , с символьными — сравнение, с табличными (или массивами) — чтение или запись элемента таблицы с заданным индексом и т.п. Как правило, в любом современном языке имеется базовый набор типов и несколько конструкций, которые позволяют строить новые типы из уже созданных. Наборы базовых типов и конструкций различаются для разных языков. В описании неформального алгоритмического языка будут использоваться типы и конструкции, которые присутствуют в большинстве языков практического программирования.

Целочисленные переменные

Тип целое число является основным для любого алгоритмического языка. Связано это с тем, что содержимое ячейки памяти или регистра процессора можно рассматривать как целое число. Адреса элементов памяти также представляют собой целые числа, с их помощью записываются машинные команды и т.д. Символы представляются в компьютере целыми числами — их кодами в некоторой кодировке. Изображения также задаются массивами целых чисел: для каждой точки цветного изображения хранятся интенсивности ее красной, зеленой и синей составляющей (в большинстве случаев — в диапазоне от 0 до 255 ). Как говорят математики, целые числа даны свыше, все остальное сконструировал из них человек.

Общепринятый в программировании термин целое число или целочисленная переменная, строго говоря, не вполне корректен. Целых чисел бесконечно много, десятичная или двоичная запись целого числа может быть сколь угодно длинной и не помещаться в области памяти, отведенной под одну переменную. Целая переменная в компьютере может хранить лишь ограниченное множество целых чисел в некотором интервале. В современных компьютерах под целую переменную отводится 4 байта, т.е. 32 двоичных разряда. Она может хранить числа от нуля до 2 в 32-й степени минус 1.

Сложение и умножение значений целых переменных выполняется следующим образом: сначала производится арифметическая операция, затем старшие разряды результата, вышедшие за границу тридцати двух двоичных разрядов (т.е. четырех байтов), отбрасываются. Определенные таким образом операции удовлетворяют традиционным законам коммутативности , ассоциативности и дистрибутивности:

a+b = b+a, ab = ba (a+b) + c = a+(b+c), (ab)c = a(bc) a(b+c) = ab+ac

Кольцо вычетов по модулю m

Целочисленный тип компьютера в точности соответствует важнейшему понятию математики — понятию кольца вычетов по модулю m . В качестве m выступает число 2 32 = 4294967296 . В математике кольцо Z_m определяется следующим образом. Все множество целых чисел Z разбивается на m классов, которые называются классами эквивалентности. Каждый класс содержит числа, попарная разность которых делится на m . Первый класс содержит числа

Элементами кольца Z_m являются классы эквивалентности. Их ровно m , так что, в отличие от множества целых чисел Z , кольцо Z_m содержит конечное число элементов. Операции с классами выполняются следующим образом: надо взять по одному представителю из каждого класса, произвести операцию и определить, в какой класс попадает результат. Этот класс и будет результатом операции. Легко показать, что он не зависит от выбора представителей.

Все числа, принадлежащие одному классу эквивалентности, имеют один и тот же остаток при делении на m . Таким образом, класс эквивалентности однозначно определяется остатком от деления на m . Традиционно остаток выбирается неотрицательным, в диапазоне от 0 до m-1 . Остатки используют для обозначения классов, при этом используются квадратные скобки. Так, выражение [5] обозначает класс эквивалентности, состоящий из всех чисел, остатки которых при делении на m равны пяти. Все кольцо Z_m состоит из элементов

например, кольцо Z₅ состоит из элементов

В элементарной школьной математике результат операции остатка от деления традиционно считается неотрицательным. Операция нахождения остатка будет обозначаться знаком процента % , как в языке Си. Тогда, к примеру,

3%5 = 3, 17%5 = 2, (-3)%5 = 2, (-17)%5 = 3.

Отсюда видно, что в школьной математике не выполняется равенство

т.е. операции изменения знака и нахождения остатка не перестановочны (на математическом языке, не коммутируют друг с другом). В компьютере операция нахождения остатка от деления для отрицательных чисел определяется иначе, ее результат может быть отрицательным. В приведенных примерах результаты будут следующими:

3%5 = 3, 17%5 = 2, (-3)%5 = -3, (-17)%5 = -2.

При делении на положительное число знак остатка совпадает со знаком делимого. При таком определении тождество

справедливо. Это позволяет во многих алгоритмах не следить за знаками (так же, как в тригонометрии формулы, выведенные для углов, меньших 90 градусов, автоматически оказываются справедливыми для любых углов).

Вернемся к рассмотрению кольца Z_m . Выберем по одному представителю из каждого класса эквивалентности, которые составляют множество Z_m . Систему таких представителей называют системой остатков. Традиционно рассматривают две системы остатков: неотрицательную систему и симметричную систему. Неотрицательная система остатков состоит из элементов

Очень удобна также симметричная система остатков, состоящая из отрицательных и неотрицательных чисел, не превосходящих m/2 по абсолютной величине. Пусть

тогда симметричная система остатков при нечетном m состоит из элементов

а при четном m — из элементов

Например, при m = 5 симметричная система остатков состоит из элементов

Кольцо Z_m можно представлять состоящим из элементов, принадлежащих выбранной системе остатков. Арифметические операции определяются следующим образом: надо взять два остатка, произвести над ними операцию как над обычными целыми числами и выбрать тот остаток, который лежит в том же классе эквивалентности, что и результат операции. Например, для симметричной системы остатков множества Z₅ имеем:

1+1 = 2, 1+2 = -2, 1+(-2) = -1, 1+(-1) = 0, (-2)+2 = 0, (-2)+(-2) = 1.

Интерпретация положительных и отрицательных чисел

В кольце вычетов невозможно определить порядок, согласованный с операциями (т.е. так, чтобы, к примеру, сумма двух положительных чисел была положительной). Таким образом, в компьютере нет, строго говоря, положительных и отрицательных целых чисел, поскольку компьютерные целые числа — это на самом деле элементы кольца вычетов. Выбирая либо неотрицательную, либо симметричную систему остатков, можно интерпретировать эти числа либо как неотрицательные в диапазоне от нуля до m-1 , либо как отрицательные и положительные числа в диапазоне от -k до k , где k — целая часть от деления m на 2 .

В программировании симметричная система остатков более популярна, поскольку трудно обойтись без отрицательных чисел. При этом следует понимать, что сумма двух положительных чисел может оказаться отрицательной, или, наоборот, сумма двух отрицательных чисел — положительной. Иногда в программировании такую ситуацию называют переполнением. Привычные свойства целочисленных операций в компьютере выполняются лишь для небольших чисел, когда результат операции не превосходит числа m = 2 32 . В случае целочисленных переменных переполнение не является экстраординарной ситуацией и не приводит к аппаратным ошибкам или прерываниям. (Это, кстати, отличает компьютерные целые числа от вещественных.) Переполнение — совершенно нормальная ситуация, если вспомнить, что компьютер работает с элементами кольца вычетов по модулю m , а не с настоящими целыми числами.

Следует также отметить, что симметричная система остатков кольца Z_m в случае четного m (а m для компьютера равно 2 32 , т.е. четно) не вполне симметрична. Поскольку ноль не имеет знака, то число положительных остатков не может равняться числу отрицательных.

Какой остаток выбрать в классе эквивалентности числа k = m/2 ? Для этого элемента выполняется непривычное с точки зрения школьной математики равенство

$k+k \equiv 0 (\mod m),$

$k \equiv -k (\mod m)$

Как отрицательный остаток -k , так и положительный k в равной мере подходят для представления этого класса эквивалентности. По традиции выбирается отрицательный остаток. Таким образом, в компьютере количество отрицательных целых чисел на единицу больше, чем количество положительных. Так как m = 2 32 = 4294967296 , то k = 2 31 = 2147483648 , и симметричная система остатков состоит из элементов

-2147483648, -2147483647, . -2, -1, 0, 1, 2, . 2147483647.

В двоичном представлении старший разряд у отрицательных целых чисел равен единице, у положительных — нулю. Двоичные разряды представления целого числа в программировании нумеруют от 0 до 31 справа налево. Старший разряд имеет номер 31 и часто называется знаковым разрядом. Таким образом, знаковый разряд равен единице у всех отрицательных чисел и нулю у неотрицательных. Двоичное представление максимального по абсолютной величине отрицательного числа k состоит из единицы и тридцати одного нуля:

-2147483648₁₀ = 10000000000000000000000000000000₂

Двоичное представление числа -1 состоит из тридцати двух единиц:

-1₁₀ = 11111111111111111111111111111111₂

Двоичное представление максимального положительного числа состоит из нуля в знаковом разряде и тридцати одной единицы:

2147483647₁₀ = 01111111111111111111111111111111₂

Следует отметить, что в программировании часто используют также короткие целые числа, двоичная запись которых занимает восемь разрядов, т.е. один байт, или шестнадцать разрядов, т.е. два байта. Работа с такими короткими целыми числами поддерживается на аппаратном уровне. В языке Си однобайтовым целым числам соответствует тип char (тип char в Си — это именно целые числа, символы представляются их целочисленными кодами), двухбайтовым — тип short . Однобайтовые целые числа — это элементы кольца вычетов Z_m , где m = 2 8 = 256 . Симметричная система остатков в этом случае состоит из элементов

В случае двухбайтовых целых чисел (тип short ) m = 2 16 = 65536 , а симметричная система остатков состоит из элементов

-32768, -32767, . -2, -1, 0, 1, 2, . 32767.

Источник