Треугольник серпинского python turtle

Библиотека turtle – это расширения языка Питон, позволяющее рисовать на экране несложные рисунки. Представьте себе, что по экрану компьютера ползает маленькая черепашка (turtle) . Вы можете управлять движением черепашки, отдавая ей различные команды вида «Проползти вперед на 10 пикселей», «Повернуть направо», «Повернуть налево». После того, как вы отдадите ей команду «Начать рисовать», черепашка будет оставлять за собой след, пока не получит команду «Кончить рисовать». Управлять черепашкой можно при помощи инструкций Питона. Вот как, например, выглядит программа, рисующая квадрат:

import turtle # Подключаем модуль turtle turtle.reset() # Очищаем экран, приводим черепашку в начальное положение turtle.pendown() # Опускаем перо перо (начало рисования) turtle.forward(50) # Проползти 50 пикселей вперед turtle.left(90) # Поворот влево на 90 градусов turtle.forward(50) # Рисуем вторую сторону квадрата turtle.left(90) turtle.forward(50) # Рисуем третью сторону квадрата turtle.left(90) turtle.forward(50) # Рисуем четвертую сторону квадрата turtle.penup() # Поднять перо (закончить рисовать) turtle.forward(100) # Отвести черепашку от рисунка в сторону turtle.mainloop() # Задержать окно на экране

Документация

Основные команды для управления черепашкой

Ползаем

forward(distance) Проползти вперёд на distance пикселей; backward(distance) Проползти назад на distance пикселей; right(angle) Повернуться налево на angle градусов; left(angle) Повернуться направо на angle градусов; goto(x, y) Переместить черепашку в точку с координатами (x,y); setx(x) Установить x координату черепашки; sety(y) Установить y координату черепашки; setheading(to_angle) Повернуть черепашку под углом to_angle к вертикали (0 — наверх, 90 — направо); home() Вернуть черепашку домой — в точку, с координатами (0,0); circle(radius) Нарисовать окружность радиуса |r|, центр которой находится слева от черепашки, если r>0 и справа, если r

Рисуем

pendown() Начать рисовать; penup() Закончить рисовать; pensize(width) Установить диаметр пера в width; pencolor(colorstring) Установить цвет линии, которая рисует черепашка (например, ‘brown’ или ‘#32c18f’ ); fillcolor(colorstring) Установить цвет заполнения; begin_fill() Начать следить за черепашкой для заполнения области; end_fill() Заполнить цветом fillcolor область, пройденную черепашкой начиная с begin_fill() ; showturtle() Показать черепашку; hideturtle() Спрятать черепашку; write(text) Вывести текст text ;

Узнать про черепашку

position() Получить текущие координаты черепашки; towards(x, y) Получить угол между текущим направление черепашки и прямой от черепашки к точке (x,y); xcor() Получить x координату черепашки; ycor() Получить y координату черепашки; heading() Получить текущий угол к вертикали; distance(x, y) Получить расстояние до точки (x,y); isdown() Узнать, рисует ли сейчас черепашка; isvisible() Узнать, видима ли сейчас черепашка;

Интерактив

onkey(function, key) Выполнить функцию function (принимающей два аргумента, x и y — координаты черепашки) после нажатия кнопки key (например, ‘a’, ‘Up’, ‘space’); listen() Начать следить на нажатиями клавиш и кликами мыши; ontimer(function, time) Выполнить функцию function через time миллисекунд; textinput(title, prompt) Вывести окно с заголовком title и текстом prompt , вернуть введённое значение;

Ещё нетривиальные примеры

from turtle import * ANGLE = 170 SIZE = 200 pencolor('red') fillcolor('yellow') speed(10) begin_fill() while True: forward(SIZE) left(ANGLE) if abs(pos()) < 1: break end_fill() mainloop()

from turtle import * def square(length): for i in range(4): forward(length) left(90) def sector(radius, angle): forward(radius) left(90) circle(radius, angle) left(90) forward(radius) left(180-angle) def move(x, y): up() forward(x) left(90) forward(y) right(90) down() def radioactive(radius1, radius2, side, angle=60, outlinecol="black", fillcol="yellow"): color(outlinecol) move(-(side/2), -(side/2)) begin_fill() square(side) color(fillcol) end_fill() move((side/2), (side/2)) color(outlinecol) right(90 + angle/2) for i in range(3): begin_fill() sector(radius1,angle) left(120) color(outlinecol) end_fill() up() forward(radius2) left(90) down() color(fillcol) begin_fill() circle(radius2) color(outlinecol) end_fill() up() left(90) forward(radius2) width(1) reset() width(5) speed(1) radioactive(160, 36, 400) mainloop()

from turtle import * bgcolor("gray60") pu() speed(0) ht() shape("square") shapesize(3.2, 3.5) shift = [10, 0, 10, 28, 10, 0, 10, 28, 10] tracer(False) for i in range(9): goto(-365 + shift[i], 267-66*i) color("black") for i in range(11): stamp() fd(70) if pencolor() == "white": color("black") else: color("white") mainloop()

from turtle import * color("orange") dot(10) center = pos() color("blue") shape("turtle") speed(0) penup() goto(200, 0) pendown() G = 800 v = Vec2D(0, 1) t = 0 dt = 1 while t < 1100: goto(pos() + v * dt) setheading(towards(center)) r = distance(center) acc = (-G / r ** 3) * pos() v += acc * dt t += dt mainloop()

from turtle import * from math import sin, cos, pi FORCE_UNIT = 0.1 # Ускорение двигателя HEIGHT = 350 WIDTH = 250 def one_step(): # Одна итерация движения global speed_x, speed_y # Глобальные переменные, в которых хранится текущая скорость cur_x, cur_y = position() # Получаем текущие координат cur_x += speed_x # Двигаем "корабль" cur_y += speed_y setpos(cur_x, cur_y) if abs(cur_x) > WIDTH: # Проверяем, что не улетели слишком далеко speed_x *= -1 if abs(cur_y) > HEIGHT: speed_y *= -1 def turn_left(): # Была нажата клавиша "Налево" left(10) def turn_right(): # Была нажата клавиша "Направо" right(10) def exit(): # Была нажата клавиша Escape, завершаем работу global continue_game continue_game = False def speed_up(): # Была нажата клавиша "Вверх" global speed_x, speed_y # Глобальные переменные, в которых хранится текущая скорость alpha = heading() * pi / 180.0 # Получаем текущий угол в радианах speed_x += FORCE_UNIT * cos(alpha) # Ускоряемся speed_y += FORCE_UNIT * sin(alpha) def main(): reset() global speed_x, speed_y # Глобальные переменные, в которых хранится текущая скорость global continue_game speed_x = speed_y = 0 continue_game = True speed(0) # Перемещаться будем мгновенно pensize(2) # И рисовать за собой линию shape("turtle") # Форма курсора fillcolor("blue") # Цвет черепашки pencolor("red") # Цвет линии onkeypress(turn_left, "Left") # По нажатию кнопки "Налево" вызвать функцию turnleft() onkeypress(turn_right, "Right") # . onkeypress(speed_up, "Up") # . onkey(exit, "Escape") # По нажатию кнопки Escape завершить работу listen() # Начинаем "слушать" нажатия клавиш while continue_game: one_step() # Запускаем основной цикл bye() main()

from turtle import * def switchpen(): if isdown(): pu() else: pd() def demo2(): """Demo of some new features.""" speed(1) st() pensize(3) setheading(towards(0, 0)) radius = distance(0, 0)/2.0 rt(90) for _ in range(18): switchpen() circle(radius, 10) write("wait a moment. ") while undobufferentries(): undo() reset() lt(90) colormode(255) laenge = 10 pencolor("green") pensize(3) lt(180) for i in range(-2, 16): if i > 0: begin_fill() fillcolor(255-15*i, 0, 15*i) for _ in range(3): fd(laenge) lt(120) end_fill() laenge += 10 lt(15) speed((speed()+1)%12) #end_fill() lt(120) pu() fd(70) rt(30) pd() color("red","yellow") speed(0) begin_fill() for _ in range(4): circle(50, 90) rt(90) fd(30) rt(90) end_fill() lt(90) pu() fd(30) pd() shape("turtle") tri = getturtle() tri.resizemode("auto") turtle = Turtle() turtle.resizemode("auto") turtle.shape("turtle") turtle.reset() turtle.left(90) turtle.speed(0) turtle.up() turtle.goto(280, 40) turtle.lt(30) turtle.down() turtle.speed(6) turtle.color("blue","orange") turtle.pensize(2) tri.speed(6) setheading(towards(turtle)) count = 1 while tri.distance(turtle) > 4: turtle.fd(3.5) turtle.lt(0.6) tri.setheading(tri.towards(turtle)) tri.fd(4) if count % 20 == 0: turtle.stamp() tri.stamp() switchpen() count += 1 tri.write("CAUGHT! ", font=("Arial", 16, "bold"), align="right") tri.pencolor("black") tri.pencolor("red") def baba(xdummy, ydummy): clearscreen() bye() while undobufferentries(): tri.undo() turtle.undo() tri.fd(50) tri.write(" Click me!", font = ("Courier", 12, "bold") ) tri.onclick(baba, 1) demo2()

Источник

5.8. Sierpinski Triangle¶

Another fractal that exhibits the property of self-similarity is the Sierpinski triangle. An example is shown in Figure 3 . The Sierpinski triangle illustrates a three-way recursive algorithm. The procedure for drawing a Sierpinski triangle by hand is simple. Start with a single large triangle. Divide this large triangle into four new triangles by connecting the midpoint of each side. Ignoring the middle triangle that you just created, apply the same procedure to each of the three corner triangles. Each time you create a new set of triangles, you recursively apply this procedure to the three smaller corner triangles. You can continue to apply this procedure indefinitely if you have a sharp enough pencil. Before you continue reading, you may want to try drawing the Sierpinski triangle yourself, using the method described.

Since we can continue to apply the algorithm indefinitely, what is the base case? We will see that the base case is set arbitrarily as the number of times we want to divide the triangle into pieces. Sometimes we call this number the “degree” of the fractal. Each time we make a recursive call, we subtract 1 from the degree until we reach 0. When we reach a degree of 0, we stop making recursive calls. The code that generated the Sierpinski Triangle in Figure 3 is shown in ActiveCode 1 .

The program in ActiveCode 1 follows the ideas outlined above. The first thing sierpinski does is draw the outer triangle. Next, there are three recursive calls, one for each of the new corner triangles we get when we connect the midpoints. Once again we make use of the standard turtle module that comes with Python. You can learn all the details of the methods available in the turtle module by using help('turtle') from the Python prompt.

Look at the code and think about the order in which the triangles will be drawn. While the exact order of the corners depends upon how the initial set is specified, let’s assume that the corners are ordered lower left, top, lower right. Because of the way the sierpinski function calls itself, sierpinski works its way to the smallest allowed triangle in the lower-left corner, and then begins to fill out the rest of the triangles working back. Then it fills in the triangles in the top corner by working toward the smallest, topmost triangle. Finally, it fills in the lower-right corner, working its way toward the smallest triangle in the lower right.

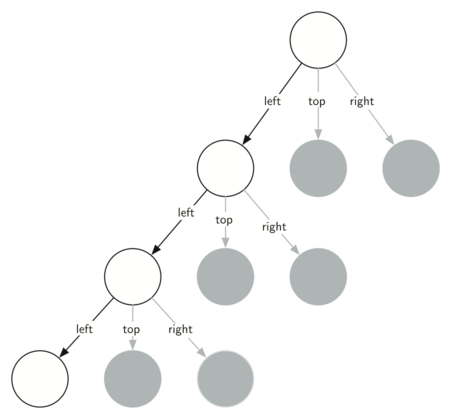
Sometimes it is helpful to think of a recursive algorithm in terms of a diagram of function calls. Figure 4 shows that the recursive calls are always made going to the left. The active functions are outlined in black, and the inactive function calls are in gray. The farther you go toward the bottom of Figure 4 , the smaller the triangles. The function finishes drawing one level at a time; once it is finished with the bottom left it moves to the bottom middle, and so on.

The sierpinski function relies heavily on the getMid function. getMid takes as arguments two endpoints and returns the point halfway between them. In addition, ActiveCode 1 has a function that draws a filled triangle using the begin_fill and end_fill turtle methods.

Источник