Tree structures in javascript

Tree data structure in JavaScript

Tree is an interesting data structure. It has wide variety of applications in all sorts of fields. For example:

• DOM is a tree data structure
• Directory and files in our OS can be represented as trees
• A family hierarchy can be represented as a tree.

There are bunch of variations of tree (such as heaps, BST etc.) which can be used in solving problems related to scheduling, image processing, databases etc. Many of complex problems may not seem related to tree on a quick look, but can actually be represented as one. We’ll walk through such problems as well (in later parts of this series) to see how trees can make seemingly complex problems much easier to comprehend and solve.

Don’t forget to subscribe to my newsletter (subscription form should be at the top of this article) if you’d like to be informed about further posts in this series.

Introduction

Implementing a Node for a binary tree is pretty straightforward.

function Node(value)< this.value = value this.left = null this.right = null > // usage const root = new Node(2) root.left = new Node(1) root.right = new Node(3) 

So these few lines of code would create a binary tree for us which looks like this:

 2 / \ / \ 1 3 / \ / \ null null null null 

Cool! So that was easy. Now, how do we put this to use?

Traversal

Let’s start with trying to walk through these connected tree nodes (or a tree). Just as we can iterate through an array, it would be cool if we can ‘iterate’ through tree nodes as well. However, trees are not linear data structures like arrays, so there isn’t just one way of traversing these. We can broadly classify the traversal approaches into following:

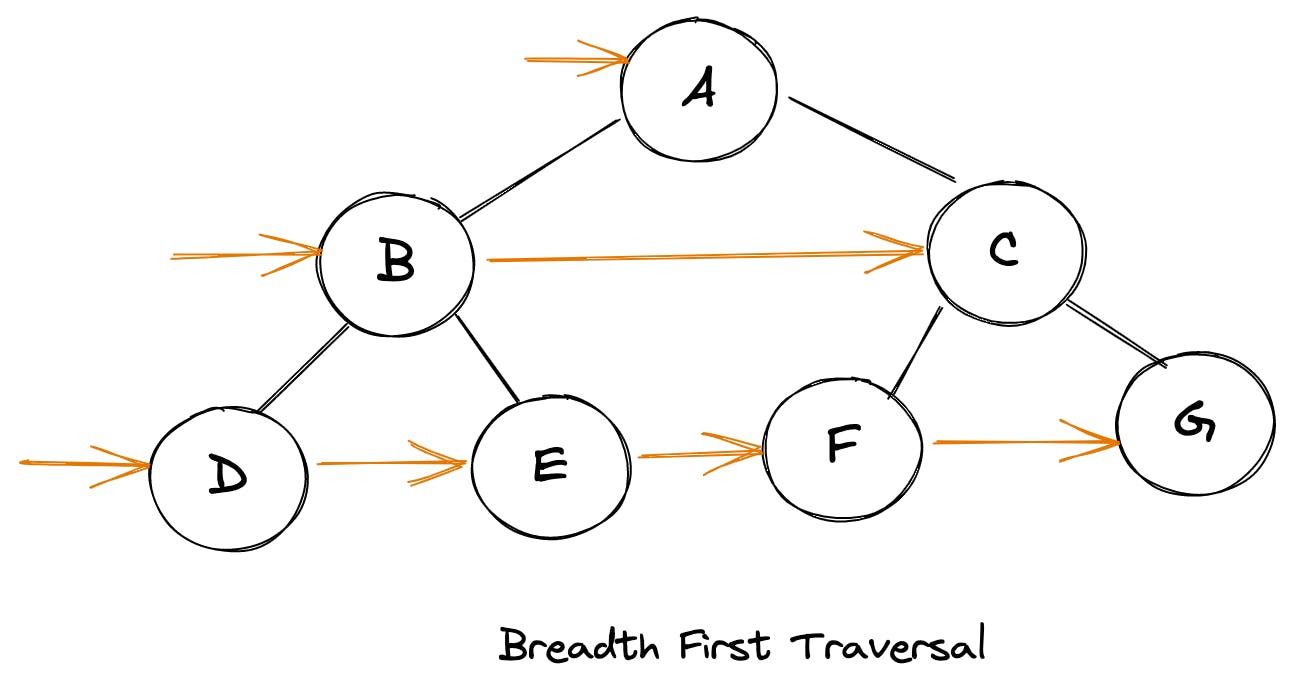
Breadth First Search/Traversal (BFS)

In this approach, we traverse the tree level by level. We would start at the root, then cover all of it’s children, and we cover all of 2nd level children, so on and so forth. For example for the tree above, traversal would result in something like this:

Here’s an illustration with slightly complex tree to make this even simpler to understand:

To achieve this form of traversal we can use a queue (First In First Out) data structure. Here’s how the overall algorithm would look like:

1. Initiate a queue with root in it
2. Remove the first item out of queue
3. Push the left and right children of popped item into the queue
4. Repeat steps 2 and 3 until the queue is empty

Here’s how this algorithm would look like post implementation:

function walkBFS(root)< if(root === null) return const queue = [root] while(queue.length)< const item = queue.shift() // do something console.log(item) if(item.left) queue.push(item.left) if(item.right) queue.push(item.right) > > 

We can modify above algorithm slightly to return an array of arrays, where each inner array represents a level with elements within in:

function walkBFS(root)< if(root === null) return const queue = [root], ans = [] while(queue.length)< const len = queue.length, level = [] for(let i = 0; i < len; i++)< const item = queue.shift() level.push(item) if(item.left) queue.push(item.left) if(item.right) queue.push(item.right) > ans.push(level) > return ans > 

Depth First Search/Traversal (DFS)

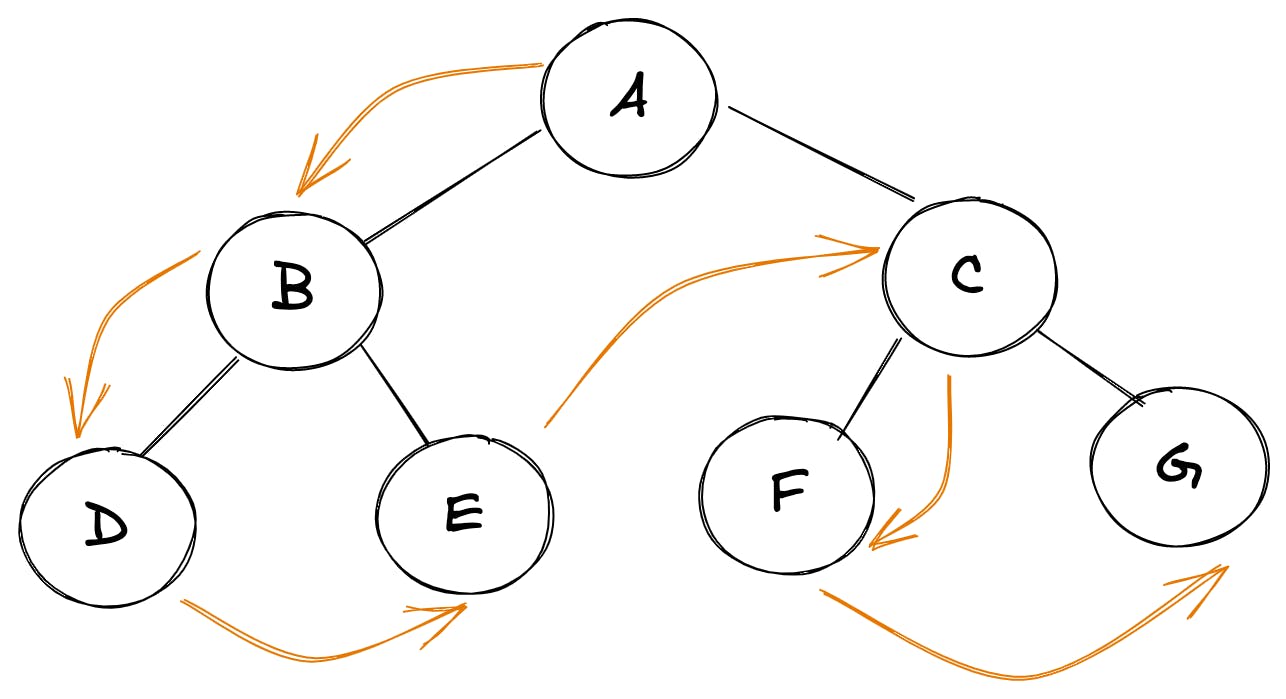
In DFS, we take one node and keep exploring it’s children until the depth the fully exhausted. It can be done in one of following ways:

 root node -> left node -> right node // pre-order traversal left node -> root node -> right node // in-order traversal left node -> right node -> root node // post-order traversal 

All of these traversal techniques can be implemented recursively as well as iteratively. Let’s jump into the implementation details:

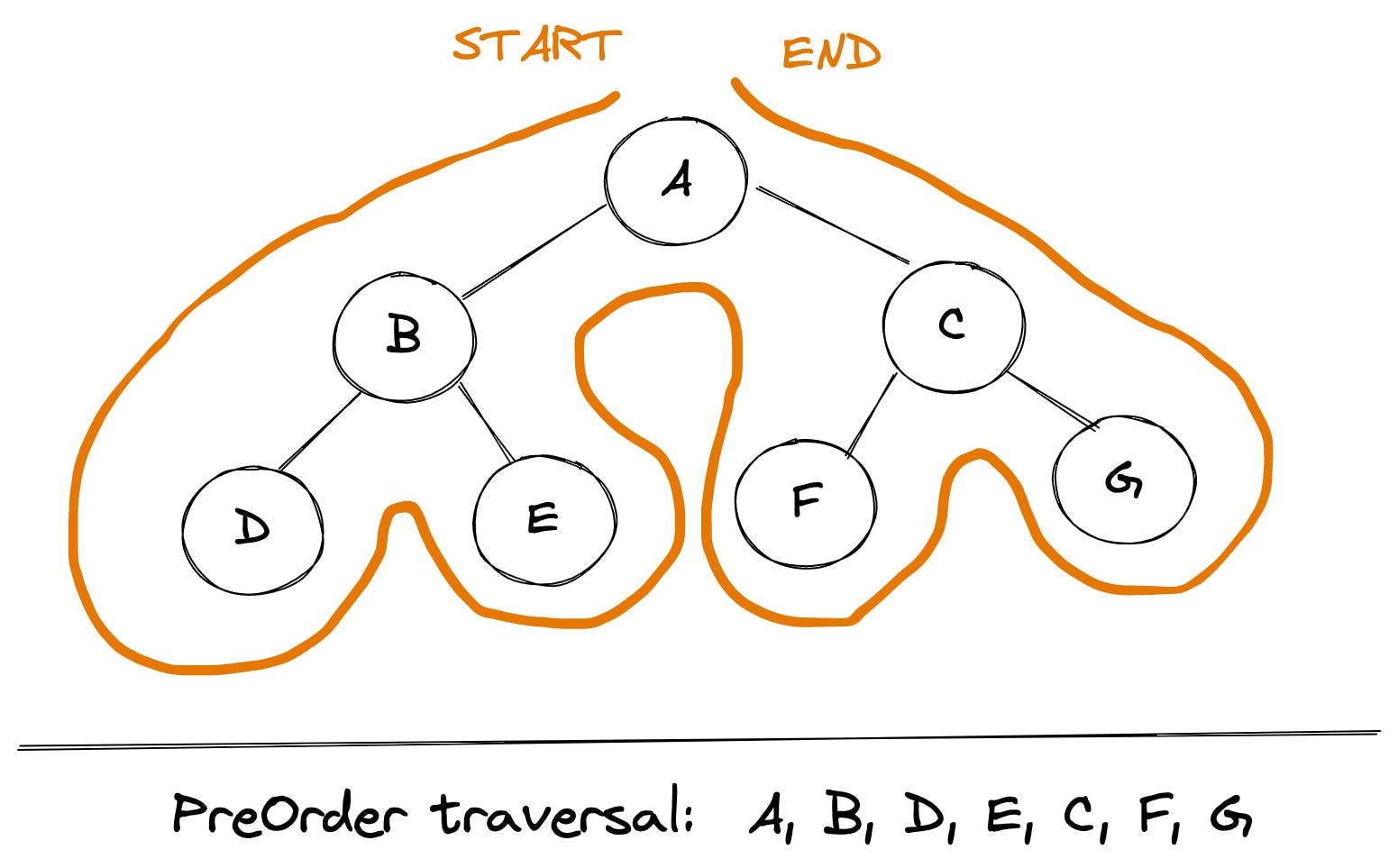
Pre-Order traversal

Here’s how PreOrder traversal looks like for a tree:

 root node -> left node -> right node 

Trick:

We can use this simple trick to find out the PreOrder traversal of any tree manually: traverse the entire tree starting from the root node keeping yourself to the left.

Implementation:

Let’s dive into actual implementation for such a traversal. Recursive approach is fairly intuitive.

function walkPreOrder(root)< if(root === null) return // do something here console.log(root.val) // recurse through child nodes if(root.left) walkPreOrder(root.left) if(root.right) walkPreOrder(root.right) > 

Iterative approach for PreOrder traversal is very similar to BFS, except we use a stack instead of a queue and we push the right child first into the stack:

function walkPreOrder(root)< if(root === null) return const stack = [root] while(stack.length)< const item = stack.pop() // do something console.log(item) // Left child is pushed after right one, since we want to print left child first hence it must be above right child in the stack if(item.right) stack.push(item.right) if(item.left) stack.push(item.left) > > 

In-Order traversal

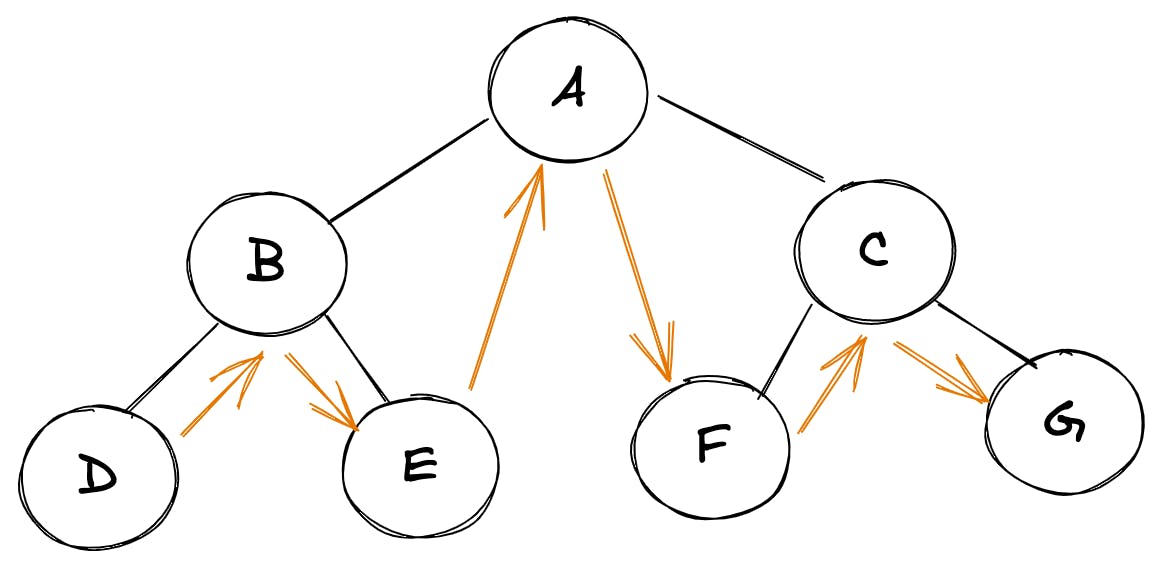
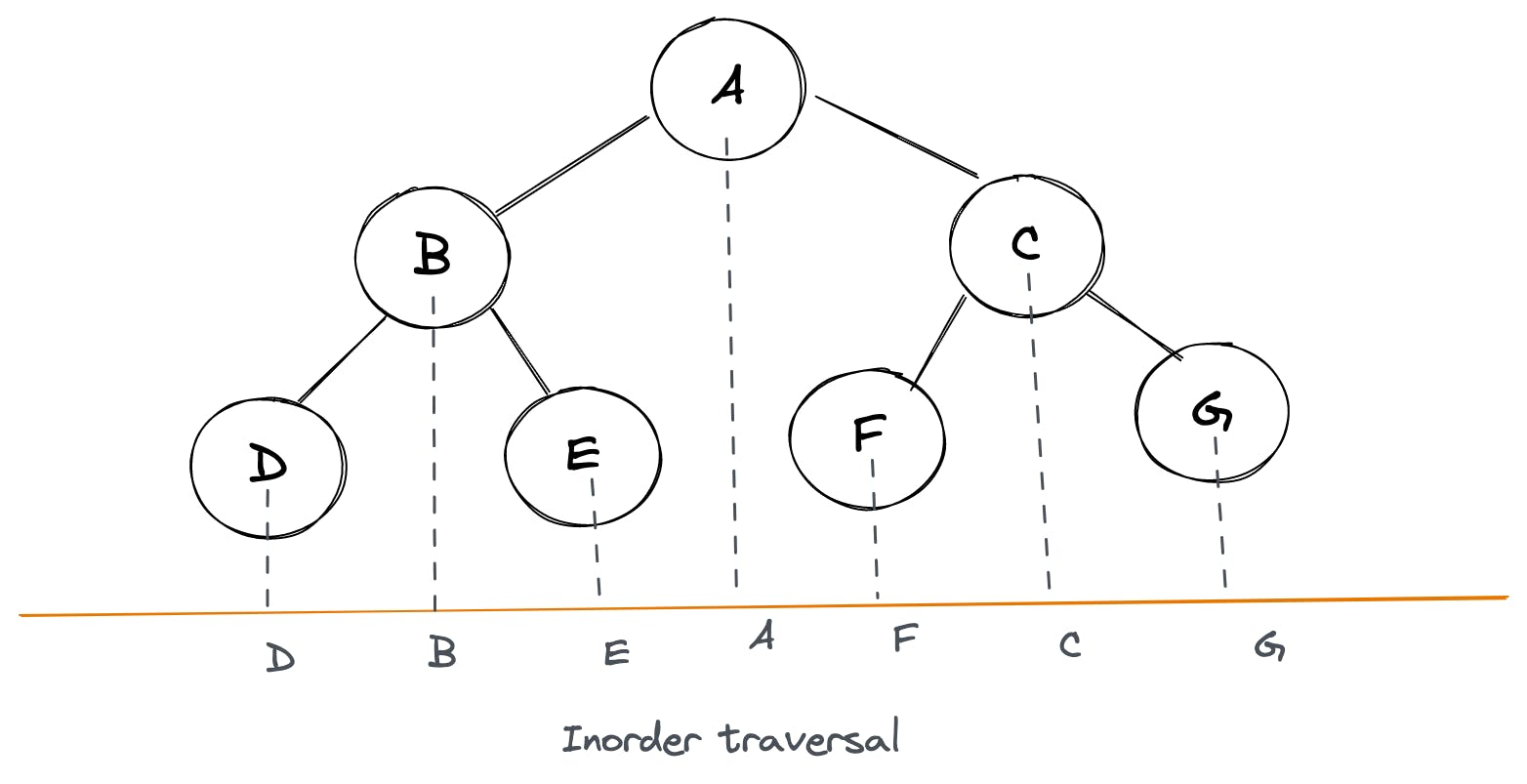
Here’s how InOrder traversal looks like for a tree:

left node -> root node -> right node 

Trick:

We can use this simple trick to find out InOrder traversal of any tree manually: keep a plane mirror horizontally at the bottom of the tree and take the projection of all the nodes.

Implementation:

function walkInOrder(root)< if(root === null) return if(root.left) walkInOrder(root.left) // do something here console.log(root.val) if(root.right) walkInOrder(root.right) > 

Iterative: This algorithm may seem a bit cryptic at first. But it’s fairly intuitive. Let’s look at it this way: in InOrder traversal left most child is printed first, then root and then right children. So first thought would be to come up with something like this:

const curr = root while(curr)< while(curr.left)< curr = curr.left // get to leftmost child > console.log(curr) // print it curr = curr.right // now move to right child > 

In the above approach we’re not able to backtrack however i.e. go back to parent nodes which led to left most nodes. So we’ll need a stack to record those. Hence our revised approach may look like:

const stack = [] const curr = root while(stack.length || curr)< while(curr)< stack.push(curr) // keep recording the trail, to backtrack curr = curr.left // get to leftmost child > const leftMost = stack.pop() console.log(leftMost) // print it curr = leftMost.right // now move to right child > 

Now we can use the above approach to lay down the final iterative algorithm:

function walkInOrder(root)< if(root === null) return const stack = [] let current = root while(stack.length || current)< while(current) < stack.push(current) current = current.left >const last = stack.pop() // do something console.log(last) current = last.right > > 

Post-Order traversal

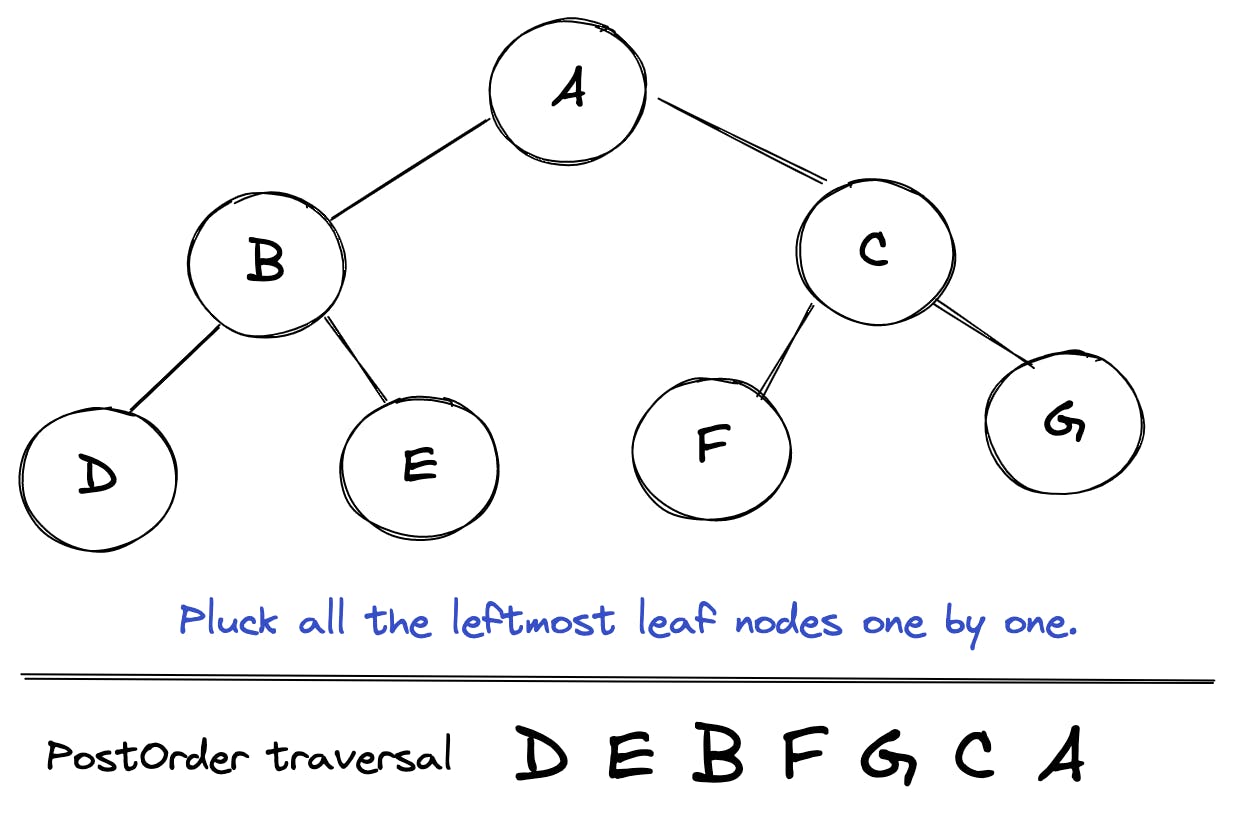
Here’s how postOrder traversal looks like for a tree:

 left node -> right node -> root node 

Trick:

For quick manual PostOrder traversal of any tree: pluck all the leftmost leaf nodes one by one.

Implementation:

Let’s dive into actual implementation for such a traversal.

function walkPostOrder(root)< if(root === null) return if(root.left) walkPostOrder(root.left) if(root.right) walkPostOrder(root.right) // do something here console.log(root.val) > 

Iterative: We already have iterative algorithm for preOrder traversal. Can we use that? Since PostOrder traversal seems to be just reverse of PreOrder traversal. Let’s see:

// PreOrder: root -> left -> right // Reverse of PreOrder: right -> left -> root // But PostOrder is: left -> right -> root 

Ah! So there’s a slight difference. But we can accomodate that by modifying our PreOrder algorithm slightly and then reversing it should give the PostOrder results. Overall algorithm would be:

// record result using root -> right -> left // reverse result left -> right -> root 

• Use a similar approach to the iterative preOrder algorithm above, using a temporary stack .
  • Only exception is we go root -> right -> left instead of root -> left -> right

  function walkPostOrder(root)< if(root === null) return [] const tempStack = [root], result = [] while(tempStack.length)< const last = tempStack.pop() result.push(last) if(last.left) tempStack.push(last.left) if(last.right) tempStack.push(last.right) > return result.reverse() > 

  Bonus: JavaScript tip

  How nice it would be if we could traverse the tree in the following way:

   for(let node of walkPreOrder(tree) )< console.log(node) > 

  Looks really nice and pretty simple to read, isn’t it? All we’ve got to do is use a walk function, which would return an iterator.

  Here’s how we can modify our walkPreOrder function above to behave as per the example shared above:

   function* walkPreOrder(root)< if(root === null) return const stack = [root] while(stack.length)< const item = stack.pop() yield item if(item.right) stack.push(item.right) if(item.left) stack.push(item.left) > > 

  Did you find this article valuable?

  Support Anish Kumar by becoming a sponsor. Any amount is appreciated!

  Источник

  Data Structures With JavaScript: Tree

  

  Cho S. Kim Last updated Jan 13, 2022

  

  Trees are one of the most commonly used data structures in web development. This statement holds true for both developers and users. Every web developer who has written HTML and loaded it into a web browser has created a tree, which is referred to as the Document Object Model (DOM). Every user of the Internet who has, in turn, consumed information on the Internet has received it in the form of a tree—the DOM.

  That’s right, the article that you are reading at this moment is rendered in your browser as a tree! The paragraph that you are reading is represented as text in a

  element; the

  element is nested inside a element; and the element is nested inside an element.

  

  The nesting of data is similar to a family tree. The element is a parent, the element is a child, and the

  element is a child of the element. If this analogy of a tree seems useful to you, then you will find comfort in knowing that more analogies will be used during our implementation of a tree.

  In this article, we will create a tree using two different methods of tree traversal: depth-first search (DFS) and breadth-first search (BFS). (If the word traversal is unfamiliar to you, consider it to mean visiting every node of the tree.) Both of these types of traversals highlight different ways of interacting with a tree; both travels, moreover, incorporate the use of data structures that we’ve covered in this series. DFS uses a stack and BFS uses a queue to visit nodes. That’s cool!

  Traversing a Tree With Depth-First Search and Breadth-First Search

  In computer science, a tree is a data structure that simulates hierarchical data with nodes. Each node of a tree holds its own data and pointers to other nodes.

  The terminology of nodes and pointers may be new to some readers, so let’s describe them further with an analogy. Let’s compare a tree to an organizational chart. The chart has a top-level position (root node), such as CEO. Directly underneath this position are other positions, such as vice president (VP).

  

  To represent this relationship, we use arrows that point from the CEO to a VP. A position, such as the CEO, is a node; the relationship we create from a CEO to a VP is a pointer. To create more relationships in our organizational chart, we just repeat this process—we have a node point to another node.

  On a conceptual level, I hope that nodes and pointers make sense. On a practical level, we can benefit from using a more technical example. Let’s consider the DOM. A DOM has an element as its top-level position (root node). This node points to a element and a element. This structure is repeated for all nodes in the DOM.

  element, for instance, can have many
  • elements nested inside it; moreover, each
  • element can have sibling
  • nodes.

  Depth-First Search (DFS)

  The depth-first search or DFS starts at the initial node and goes deeper into the tree until the desired element or an element with no children—a leaf—is found. And then, it backtracks from the leaf node and visits the most recent node that is not yet explored.

  

  Breadth-First Search (BFS)

  In a breadth-first search, the tree traversal starts from the root node and first traverses all the neighboring nodes. Then, it selects the nearest node and explores the new nodes. This method is repeated for each node until it reaches the destination.

  

  Operations of a Tree

  Since every tree contains nodes, which can be a separate constructor from a tree, we will outline the operations of both constructors: Node and Tree .

  Node

  • data stores a value
  • parent points to a node’s parent
  • children points to the next node in the list

  Tree

  • _root points to the root node of a tree
  • find(data) : return the node containing the given data
  • add(data, parentData) : add a new node to the parent containing the given data
  • remove(data) : remove the node containing the given data
  • forEach(callback) : run a callback on each node of the tree in depth-first order
  • forEachBreathFirst(callback) : run a callback on each node of the tree in breadth-first order

  Implementing a Tree in JavaScript

  Now let’s write the code for a tree!

  The Node Class

  For our implementation, we will first define a class named Node and then a constructor named Tree .

  Источник