Tree building in java

Data structures 101: A deep dive into trees with Java

Data structures are an important part of programming and coding interviews. These skills show your ability to think complexly, solve ambiguous problems, and recognize coding patterns.

Programmers use data structures to organize data, so the more efficient your data structures are, the better your programs will be.

Today, we will take a deep dive into one of the most popular data structures out there: trees.

Today, we will cover:

Get hands-on with data structures

Data structures are amongst the fundamentals of Computer Science and an important decision in every program. Consequently, they are also largely categorized as a vital benchmark of computer science knowledge when it comes to industry interviews. This course contains a detailed review of all the common data structures and provides implementation level details in Java to allow readers to become well equipped. Now with more code solutions, lessons, and illustrations than ever, this is the course for you!

What is a tree?

Data structures are used to store and organize data. We can use algorithms to manipulate and use our data structures. Different types of data are organized more efficiently by using different data structures.

Trees are non-linear data structures. They are often used to represent hierarchical data. For a real-world example, a hierarchical company structure uses a tree to organize.

Components of a Tree

Trees are a collection of nodes (vertices), and they are linked with edges (pointers), representing the hierarchical connections between the nodes. A node contains data of any type, but all the nodes must be of the same data type. Trees are similar to graphs, but a cycle cannot exist in a tree. What are the different components of a tree?

Root: The root of a tree is a node that has no incoming link (i.e. no parent node). Think of this as a starting point of your tree.

Children: The child of a tree is a node with one incoming link from a node above it (i.e. a parent node). If two children nodes share the same parent, they are called siblings.

Parent: The parent node has an outgoing link connecting it to one or more child nodes.

Leaf: A leaf has a parent node but has no outgoing link to a child node. Think of this as an endpoint of your tree.

Subtree: A subtree is a smaller tree held within a larger tree. The root of that tree can be any node from the bigger tree.

Depth: The depth of a node is the number of edges between that node and the root. Think of this as how many steps there are between your node and the tree’s starting point.

Height: The height of a node is the number of edges in the longest path from a node to a leaf node. Think of this as how many steps there are between your node and the tree’s endpoint. The height of a tree is the height of its root node.

Degree: The degree of a node refers to the number of sub-trees.

Источник

Implementing a Binary Tree in Java

As always, the writeup is super practical and based on a simple application that can work with documents with a mix of encrypted and unencrypted fields.

We rely on other people’s code in our own work. Every day.

It might be the language you’re writing in, the framework you’re building on, or some esoteric piece of software that does one thing so well you never found the need to implement it yourself.

The problem is, of course, when things fall apart in production — debugging the implementation of a 3rd party library you have no intimate knowledge of is, to say the least, tricky.

Lightrun is a new kind of debugger.

It’s one geared specifically towards real-life production environments. Using Lightrun, you can drill down into running applications, including 3rd party dependencies, with real-time logs, snapshots, and metrics.

Learn more in this quick, 5-minute Lightrun tutorial:

Slow MySQL query performance is all too common. Of course it is. A good way to go is, naturally, a dedicated profiler that actually understands the ins and outs of MySQL.

The Jet Profiler was built for MySQL only, so it can do things like real-time query performance, focus on most used tables or most frequent queries, quickly identify performance issues and basically help you optimize your queries.

Critically, it has very minimal impact on your server’s performance, with most of the profiling work done separately — so it needs no server changes, agents or separate services.

Basically, you install the desktop application, connect to your MySQL server, hit the record button, and you’ll have results within minutes:

DbSchema is a super-flexible database designer, which can take you from designing the DB with your team all the way to safely deploying the schema.

The way it does all of that is by using a design model, a database-independent image of the schema, which can be shared in a team using GIT and compared or deployed on to any database.

And, of course, it can be heavily visual, allowing you to interact with the database using diagrams, visually compose queries, explore the data, generate random data, import data or build HTML5 database reports.

Get started with Spring 5 and Spring Boot 2, through the Learn Spring course:

> CHECK OUT THE COURSE

1. Introduction

In this tutorial, we’ll cover the implementation of a binary tree in Java.

For the sake of this tutorial, we’ll use a sorted binary tree that contains int values.

Further reading:

How to Print a Binary Tree Diagram

Reversing a Binary Tree in Java

Depth First Search in Java

2. Binary Tree

A binary tree is a recursive data structure where each node can have 2 children at most.

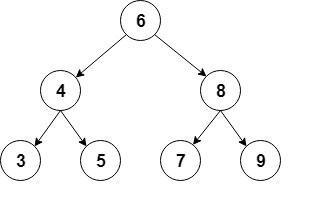
A common type of binary tree is a binary search tree, in which every node has a value that is greater than or equal to the node values in the left sub-tree, and less than or equal to the node values in the right sub-tree.

Here’s a visual representation of this type of binary tree:

For the implementation, we’ll use an auxiliary Node class that will store int values, and keep a reference to each child:

Then we’ll add the starting node of our tree, usually called the root:

3. Common Operations

Now let’s see the most common operations we can perform on a binary tree.

3.1. Inserting Elements

The first operation we’re going to cover is the insertion of new nodes.

First, we have to find the place where we want to add a new node in order to keep the tree sorted. We’ll follow these rules starting from the root node:

• if the new node’s value is lower than the current node’s, we go to the left child
• if the new node’s value is greater than the current node’s, we go to the right child
• when the current node is null, we’ve reached a leaf node and we can insert the new node in that position

Then we’ll create a recursive method to do the insertion:

private Node addRecursive(Node current, int value) < if (current == null) < return new Node(value); >if (value < current.value) < current.left = addRecursive(current.left, value); >else if (value > current.value) < current.right = addRecursive(current.right, value); >else < // value already exists return current; >return current; >

Next we’ll create the public method that starts the recursion from the root node:

Let’s see how we can use this method to create the tree from our example:

private BinaryTree createBinaryTree()

3.2. Finding an Element

Now let’s add a method to check if the tree contains a specific value.

As before, we’ll first create a recursive method that traverses the tree:

private boolean containsNodeRecursive(Node current, int value) < if (current == null) < return false; >if (value == current.value) < return true; >return value

Here we’re searching for the value by comparing it to the value in the current node; we’ll then continue in the left or right child depending on the outcome.

Next we’ll create the public method that starts from the root:

public boolean containsNode(int value)

Then we’ll create a simple test to verify that the tree really contains the inserted elements:

@Test public void givenABinaryTree_WhenAddingElements_ThenTreeContainsThoseElements()

All the nodes added should be contained in the tree.

3.3. Deleting an Element

Another common operation is the deletion of a node from the tree.

First, we have to find the node to delete in a similar way as before:

private Node deleteRecursive(Node current, int value) < if (current == null) < return null; >if (value == current.value) < // Node to delete found // . code to delete the node will go here >if (value < current.value) < current.left = deleteRecursive(current.left, value); return current; >current.right = deleteRecursive(current.right, value); return current; >

Once we find the node to delete, there are 3 main different cases:

• a node has no children – this is the simplest case; we just need to replace this node with null in its parent node
• a node has exactly one child – in the parent node, we replace this node with its only child.
• a node has two children – this is the most complex case because it requires a tree reorganization

Let’s see how we would implement the first case when the node is a leaf node:

if (current.left == null && current.right == null)

Now let’s continue with the case when the node has one child:

if (current.right == null) < return current.left; >if (current.left == null)

Here we’re returning the non-null child so it can be assigned to the parent node.

Finally, we have to handle the case where the node has two children.

First, we need to find the node that will replace the deleted node. We’ll use the smallest node of the soon to be deleted node’s right sub-tree:

private int findSmallestValue(Node root)

Then we assign the smallest value to the node to delete, and after that, we’ll delete it from the right sub-tree:

int smallestValue = findSmallestValue(current.right); current.value = smallestValue; current.right = deleteRecursive(current.right, smallestValue); return current;

Finally, we’ll create the public method that starts the deletion from the root:

public void delete(int value)

Now let’s check that the deletion worked as expected:

@Test public void givenABinaryTree_WhenDeletingElements_ThenTreeDoesNotContainThoseElements()

4. Traversing the Tree

In this section, we’ll explore different ways of traversing a tree, covering in detail the depth-first and breadth-first searches.

We’ll use the same tree that we used before, and we’ll examine the traversal order for each case.

4.1. Depth-First Search

Depth-first search is a type of traversal that goes deep as much as possible in every child before exploring the next sibling.

There are several ways to perform a depth-first search: in-order, pre-order and post-order.

The in-order traversal consists of first visiting the left sub-tree, then the root node, and finally the right sub-tree:

public void traverseInOrder(Node node) < if (node != null) < traverseInOrder(node.left); System.out.print(" " + node.value); traverseInOrder(node.right); >>

If we call this method, the console output will show the in-order traversal:

Pre-order traversal visits first the root node, then the left sub-tree, and finally the right sub-tree:

public void traversePreOrder(Node node) < if (node != null) < System.out.print(" " + node.value); traversePreOrder(node.left); traversePreOrder(node.right); >>

Let’s check the pre-order traversal in the console output:

Post-order traversal visits the left sub-tree, the right subt-ree, and the root node at the end:

public void traversePostOrder(Node node) < if (node != null) < traversePostOrder(node.left); traversePostOrder(node.right); System.out.print(" " + node.value); >>

Here are the nodes in post-order:

4.2. Breadth-First Search

This is another common type of traversal that visits all the nodes of a level before going to the next level.

This kind of traversal is also called level-order, and visits all the levels of the tree starting from the root, and from left to right.

For the implementation, we’ll use a Queue to hold the nodes from each level in order. We’ll extract each node from the list, print its values, then add its children to the queue:

public void traverseLevelOrder() < if (root == null) < return; >Queue nodes = new LinkedList<>(); nodes.add(root); while (!nodes.isEmpty()) < Node node = nodes.remove(); System.out.print(" " + node.value); if (node.left != null) < nodes.add(node.left); >if (node.right != null) < nodes.add(node.right); >> >

In this case, the order of the nodes will be:

5. Conclusion

In this article, we learned how to implement a sorted binary tree in Java, and its most common operations.

The full source code for the examples is available over on GitHub.

Slow MySQL query performance is all too common. Of course it is. A good way to go is, naturally, a dedicated profiler that actually understands the ins and outs of MySQL.

The Jet Profiler was built for MySQL only, so it can do things like real-time query performance, focus on most used tables or most frequent queries, quickly identify performance issues and basically help you optimize your queries.

Critically, it has very minimal impact on your server’s performance, with most of the profiling work done separately — so it needs no server changes, agents or separate services.

Basically, you install the desktop application, connect to your MySQL server, hit the record button, and you’ll have results within minutes:

Источник