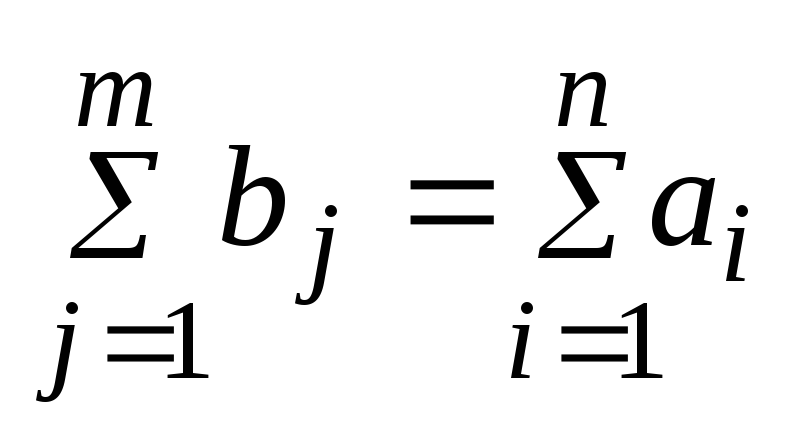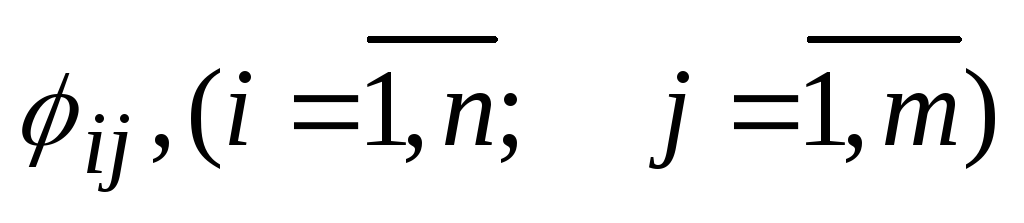Транспортная задача линейного программирования метод фогеля

3. Метод аппроксимации Фогеля

Основным недостатком метода минимального элемента является неучет будущих тарифов: в первых шагах алгоритма тарифы минимальны, на заключительных шагах возможно использование перевозок с высокими тарифами, тем самым, опорный план будетотличаться от оптимального, хотя и не так сильно, какв методе северо-западного угла.

Метод аппроксимации Фогеля лишен выше указанных недостатков, однако довольно сложен для исполнения по сравнению двумя предыдущими методами.

Алгоритм метода Фогеля состоит в следующем:

1. На каждой итерации вычисляют по всем столбцам и строкам разность между двумя записанными в них минимальными тарифами,
2. Среди указанных разностей выбирают максимальную.
3. В строке (или столбце) с выбранной разностью определяют минимальный тариф и заполняют ее, полностью удовлетворяя потребности или полностью исчерпав запасы.
4. Если минимальный тариф одинаков для нескольких клеток данной строки (столбца), то для заполнения выбирают ту клетку, которая расположена в столбце (строке), соответствующим (ей) наибольшей разности между двумя минимальными тарифами, находящимися в данном (ей) столбце (строке).
5. Строка с израсходованным запасом или столбец с удовлетворенной потребностью исключаются из рассмотрения, и в соответствующей разности ставится прочерк.

Рассмотрим процесс составления опорного плана по методу Фогеля. На первом шаге разности между двумя соседними минимальными тарифами равны для строк (2-1=1. 5-4=1, 3-2=1), для столбцов (7-4=3, 5-2=3, 3-1=2, 6-2=4). Максимальная разность имеет место для четвертого столбца (4). Заполняем клетку А₁B₄, удовлетворив всю потребность четвертого предприятия, в результате чего у первого поставщика останется 50 единиц сырья, а четвертый столбец исключается из дальнейшего рассмотрения (вместо разностей ставится прочерк). На втором шаге итерации вычислим разности между соседними минимальными тарифами оставшихся клеток для строк (7-1=6, 5-4=1, 3-2=1) и для столбцов (7-4=3, 5-2=3, 3-1=2). Максимальная разность будет для первой строки (6). Заполняем клетку А₁B₃, исчерпав оставшееся сырье первого поставщика, при этом третьему потребителю нужно еще 190-50=140 единиц сырья. В итоге из рассмотрения исключаем первую строку. На следующем этапе разности равны для строк (5-4=1, 3-2=1) и для столбцов (9-4=5, 5-2=3, 9-3=6). Максимальная разность у третьего столбца (6). Заполняем клетку А₃B₃, полностью удовлетворив потребности третьего предприятия, в результате чего у третьего производителя останется 170-140=30 единиц сырья. Из дальнейшего рассмотрения исключаем третий столбец. Далее разности равны для строк (5-4=1, 9-2=7) и для столбцов (9-4=5, 5-2=3). Разность максимальной будет для третьей строки. Следовательно, заполняем клетку А₃B₂, исключив из последующих шагов третью строку. На последнем шаге остается только одна разность для второй строки (5-4=1). Поэтому заполняем оставшиеся клетки данной строки в порядке возрастания тарифов, сначала клетку А₂B₁, затем А₂B₂. В результате опорный план будет задаваться следующей матрицей: , при этом общая стоимость перевозок составит: Q=1*50+2*110+4*120+5*20+2*30+3*140=1330 условных единиц. Сравнение трех методов нахождения опорного плана позволяет сделать вывод, что план, самый близкий к оптимальному, дает метод аппроксимации Фогеля.

Источник

4.3. Методы решения транспортной задачи

Постановка транспортной задачи линейного программирования

Имеется n складов и m пунктов потребления. На складах имеются запасы однотипного товара a₁, …, a_n. Пункты потребления подали заявки на количество товара b₁, …, b_m. Сумма заявок не превосходит суммы запасов (т. е. все заявки могут и должны быть выполнены). Стоимость перевозки единицы товара соi-го склада в j-й пункт равна c_ij.

Требуется составить такой план перевозок при котором все заявки были бы удовлетворены, и при этом общая стоимость всех перевозок была минимальной. Т. е. нужно определить с какого склада, в какой пункт потребления и сколько единиц товара следует перевезти, чтобы суммарная стоимость всех перевозок была минимальной при условиях, что со склада нельзя вывести товара больше, чем имеется на складе, и что все заявки пунктов потребления будут выполнены [1].

Если предположить, что , то транспортная задача называетсясбалансированной, а в противном случае – не сбалансированной транспортной задачей.

Для того чтобы не сбалансированную транспортную задачу сделать сбалансированной, следует ввести фиктивные пункты назначения (если 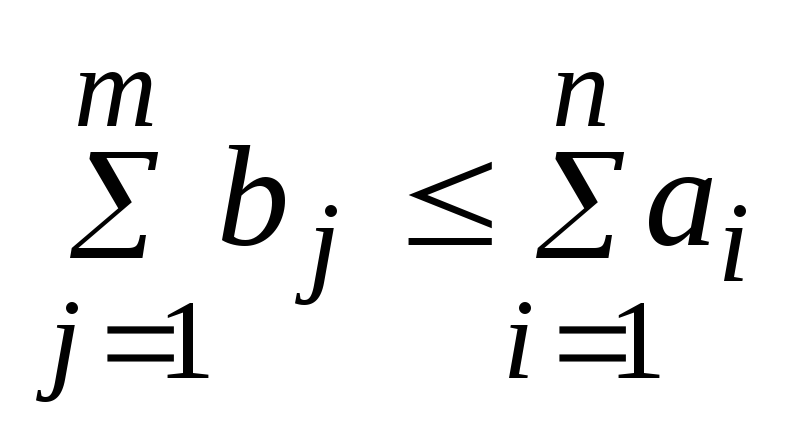) или отправления (если). Количество единиц товара, которое нужно вывезти из фиктивного пункта отправления в реальный пункт назначения говорит о том, что заявка этого пункта будет недовыполнена на это количество. Количество единиц товара, которое нужно вывезти из реального пункта отправления в фиктивный пункт назначения говорит о том, что после окончания перевозок в этом пункте останется именно это количество товара.

Выполнение баланса транспортной задачи необходимо для того, чтобы иметь возможность применить алгоритм решения, построенный на использовании транспортных таблиц.

Для сбалансированной транспортной задачи можно сформулировать целевую функцию, которую необходимо минимизировать:

при ограничениях 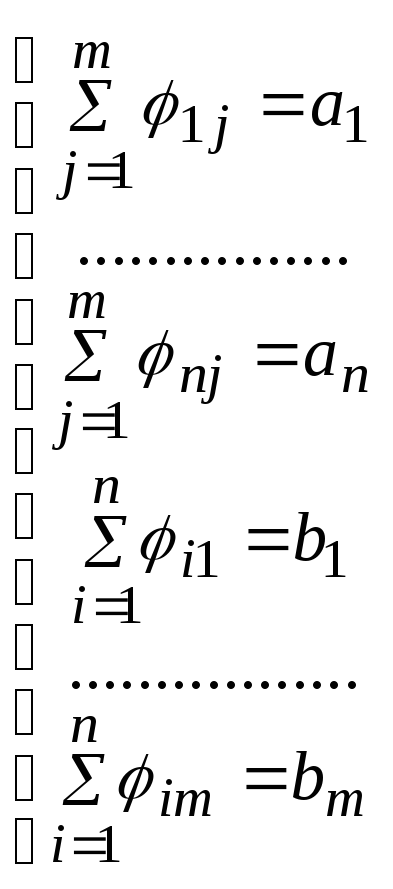и_ij  0, ,

где первая группа ограничений показывает, что количество единиц вывозимого со склада товара равно количеству единиц товара, имеющегося на складе, а вторая – что все заявки пунктов потребления должны быть выполнены.

Основные свойства транспортной задачи

линейного программирования

Поскольку в сбалансированной транспортной задаче то при сложении всех уравнений первой и второй группы мы получим одно и то же значение суммы. Это означает, что независимыми являются неm+n, а m+n-1 уравнений (т. е. одно из уравнений является избыточным). Следовательно, в транспортной задаче количество базисных переменных: а небазисных:[19].

План перевозок (план) – это любая совокупность значений .

Допустимый план перевозок – это план перевозок, который удовлетворяет балансовым условиям: все заявки удовлетворены – все запасы исчерпаны.

Опорный допустимый план перевозок – это допустимый план перевозок, в котором отличны от нуля не более перевозок, а остальные перевозки равны нулю.

Оптимальный план перевозок – это допустимый план перевозок, который приводит к минимальной стоимости всех перевозок.

Методы решения транспортной задачи сводятся к операциям с транспортной таблицей:

ПН

Источник

Метод Фогеля

Исторически математическая экономика началась с моделей простого и расширенного воспроизводства. В них отражались потоки денег и потоки товаров и продуктов. Это, например, модель Ф. Кенэ. Позднее эти модели подробно и более глубоко изучались в экономической кибернетике — здесь можно указать на работы О. Ланге. Рассмотрены схемы денежных и материальных потоков, обеспечивающих простое и расширенное воспроизводство, их идентификацию, модели математической статистики. Далее возникли концепции производственных функций, предельных и маргинальных значений, предельных полезностей и субъективных полезностей. Дальнейшее развитие — в рамках линейного и выпуклого программирования, выпуклого анализа, развитие тонких техник моделирования: имитационное моделирование, экспертные системы, нейронные сети. Транспортная задача линейного программирования получила в настоящее время широкое распространение в теоретических обработках и практическом применении на транспорте и в промышленности. Особенно важное значение она имеет в деле рационализации поставок важнейших видов промышленной и сельскохозяйственной продукции, а также оптимального планирования грузопотоков и работы различных видов транспорта.

Транспортная задача линейного программирования получила в настоящее время широкое распространение в теоретических обработках и практическом применении на транспорте и в промышленности. Особенно важное значение она имеет в деле рационализации поставок важнейших видов промышленной и сельскохозяйственной продукции, а также оптимального планирования грузопотоков и работы различных видов транспорта. Транспортная задача – это задача о наиболее экономном плане перевозок однородного продукта из пунктов производства (станций отправления) в пункты потребления (станции назначения). Определение оптимального плана транспортной задачи начинают с нахождения какого-нибудь ее опорного плана.

Опорный план является допустимым решением ТЗ и используется в качестве начального базисного решения при нахождении оптимального решения методом потенциалов. Существует три метода нахождения опорных планов: метод северо-западного угла, метод минимального элемента и метод Фогеля. «Качество» опорных планов, полученных этими методами, различается: в общем случае метод Фогеля дает наилучшее решение (зачастую

Суть метода

Метод Фогеля состоит в вычислении для каждой строки транспортной таблицы разницы между двумя наименьшими тарифами. Аналогичное действие выполняют для каждого столбца этой таблицы. Наибольшая разница между двумя минимальными тарифами соответствует наиболее предпочтительной строке или столбцу (если есть несколько строк или столбцов с одинаковой разницей, то выбор между ними произволен). В пределах этой строки или столбца отыскивают ячейку с минимальным тарифом, куда пишут отгрузку. Строки поставщиков или столбцы потребителей, которые полностью исчерпали свои возможности по отгрузке или потребности которых в товаре были удовлетворены, вычеркиваются из таблицы (в примерах ниже они закрашиваются серым цветом), и вычисление повторяются до полного удовлетворения спроса и исчерпания отгрузок без учета вычеркнутых («серых») ячеек

Алгоритм решения

Шаг 1. Составляют транспортную таблицу. Шаг 2. Для каждой строки и каждого столбца транспортной таблицы определяют разность между наименьшим тарифом и ближайшим к нему значением Шаг 3. В строке или в столбце, которым соответствует наибольшая разность, выбирают клетку с наименьшим тарифом. Шаг 4. В выбранную клетку, аналогично предыдущим методам, записывают максимально возможное число единиц продукции, которое разрешается ограничениями на предложение и спрос. После этого вычеркивают либо строку, если предложение поставщика исчерпано, либо столбец, если спрос потребителя удовлетворен. Если все клетки таблицы заполнены или вычеркнуты, то план перевозок построен. В противном случае переходят к шагу 2 без учета вычеркнутых и заполненных клеток. В методе Фогеля используются штрафы, взимаемые за неудачный «выбор» маршрута. Рассчитанные на шаге 2 разности между двумя уровнями затрат на перевозку являются штрафами за неверно выбранный маршрут перевозки.

Источник