Транспонирование матрицы python numpy

numpy.transpose#

For a 1-D array, this returns an unchanged view of the original array, as a transposed vector is simply the same vector. To convert a 1-D array into a 2-D column vector, an additional dimension must be added, e.g., np.atleast2d(a).T achieves this, as does a[:, np.newaxis] . For a 2-D array, this is the standard matrix transpose. For an n-D array, if axes are given, their order indicates how the axes are permuted (see Examples). If axes are not provided, then transpose(a).shape == a.shape[::-1] .

Parameters : a array_like

axes tuple or list of ints, optional

If specified, it must be a tuple or list which contains a permutation of [0,1,…,N-1] where N is the number of axes of a. The i’th axis of the returned array will correspond to the axis numbered axes[i] of the input. If not specified, defaults to range(a.ndim)[::-1] , which reverses the order of the axes.

Returns : p ndarray

a with its axes permuted. A view is returned whenever possible.

Move axes of an array to new positions.

Return the indices that would sort an array.

Use transpose(a, argsort(axes)) to invert the transposition of tensors when using the axes keyword argument.

>>> a = np.array([[1, 2], [3, 4]]) >>> a array([[1, 2], [3, 4]]) >>> np.transpose(a) array([[1, 3], [2, 4]]) 

>>> a = np.array([1, 2, 3, 4]) >>> a array([1, 2, 3, 4]) >>> np.transpose(a) array([1, 2, 3, 4]) 

>>> a = np.ones((1, 2, 3)) >>> np.transpose(a, (1, 0, 2)).shape (2, 1, 3) 

>>> a = np.ones((2, 3, 4, 5)) >>> np.transpose(a).shape (5, 4, 3, 2) 

Источник

numpy.matrix.transpose#

Refer to numpy.transpose for full documentation.

• None or no argument: reverses the order of the axes.
• tuple of ints: i in the j-th place in the tuple means that the array’s i-th axis becomes the transposed array’s j-th axis.
• n ints: same as an n-tuple of the same ints (this form is intended simply as a “convenience” alternative to the tuple form).

View of the array with its axes suitably permuted.

Array property returning the array transposed.

Give a new shape to an array without changing its data.

>>> a = np.array([[1, 2], [3, 4]]) >>> a array([[1, 2], [3, 4]]) >>> a.transpose() array([[1, 3], [2, 4]]) >>> a.transpose((1, 0)) array([[1, 3], [2, 4]]) >>> a.transpose(1, 0) array([[1, 3], [2, 4]]) 

>>> a = np.array([1, 2, 3, 4]) >>> a array([1, 2, 3, 4]) >>> a.transpose() array([1, 2, 3, 4]) 

Источник

numpy.ndarray.transpose#

Refer to numpy.transpose for full documentation.

• None or no argument: reverses the order of the axes.
• tuple of ints: i in the j-th place in the tuple means that the array’s i-th axis becomes the transposed array’s j-th axis.
• n ints: same as an n-tuple of the same ints (this form is intended simply as a “convenience” alternative to the tuple form).

View of the array with its axes suitably permuted.

Array property returning the array transposed.

Give a new shape to an array without changing its data.

>>> a = np.array([[1, 2], [3, 4]]) >>> a array([[1, 2], [3, 4]]) >>> a.transpose() array([[1, 3], [2, 4]]) >>> a.transpose((1, 0)) array([[1, 3], [2, 4]]) >>> a.transpose(1, 0) array([[1, 3], [2, 4]]) 

>>> a = np.array([1, 2, 3, 4]) >>> a array([1, 2, 3, 4]) >>> a.transpose() array([1, 2, 3, 4]) 

Источник

Как транспонировать матрицу в Python

Сегодня мы хотим разобрать, как транспонировать матрицу в Python. Однако сначала давайте рассмотрим, что представляет из себя матрица сама по себе и в чём заключается процесс транспонирования.

Итак, матрица состоит из строк и столбцов. Создать матрицу можно по-разному, но самый простой способ – использовать вложенные списки, как показано ниже:

Внутренние списки представляют собой строки, а каждый элемент внутри списка называется столбцом. Итак, в приведенном выше примере у нас есть две строки и три столбца, т.е. мы имеем дело с матрицей 2 на 3. Стоит помнить, что индексация Python начинается с нуля.

Транспонирование матрицы означает, что мы меняем строки на столбцы или столбцы на строки. Теперь давайте обсудим различные методы транспонирования матрицы.

Метод 1. Транспонирование матрицы с помощью NumPy transpose()

Первый метод, который мы разберем, — это использование библиотеки NumPy. NumPy в основном работает с массивами в Python, а для транспонирования мы можем вызвать метод transpose() .

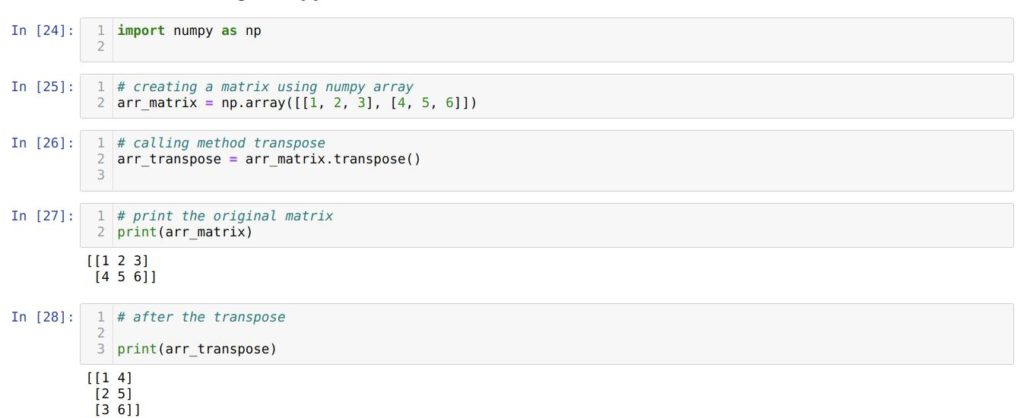
Давайте разберем всё по порядку. Для начала нам нужно импортировать модуль NumPy как np .

Дальше, в ячейке номер [25] мы создаем массив NumPy с именем arr_matrix .

В ячейке номер [26] мы вызываем метод transpose() для нашей матрицы – объекта arr_matrix , который мы создали ранее.

В ячейке номер [27] мы выводим на экран исходную матрицу arr_matrix .

А в ячейке номер [28] – транспонированную матрицу arr_transpose . Можем заметить, что в результате мы получили именно то, что нам было нужно – транспонированную матрицу.

Метод 2. Использование метода numpy.transpose()

Мы также можем транспонировать матрицу в Python с помощью numpy.transpose() . При этом мы передаем матрицу в метод transpose() в качестве аргумента.

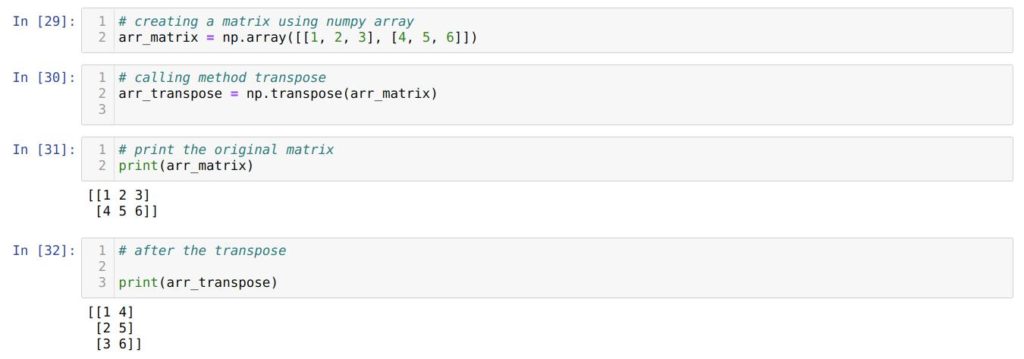
В ячейке номер [29] мы создаем матрицу, используя массив NumPy, с именем arr_matrix .

Далее мы передаем arr_matrix в метод transpose() и сохраняем результат в новую переменную arr_transpose .

В ячейке номер [31] мы печатаем исходную матрицу arr_matrix .

А дальше мы выводим на экран транспонированную матрицу arr_transpose . Получаем результат аналогичный тому, что получили в первом примере.

Метод 3. Транспонирование матрицы с использованием библиотеки SymPy

Применение библиотеки SymPy – это еще один подход к транспонированию матрицы. Эта библиотека использует символьную математику для решения алгебраических задач.

Сначала нам, конечно же, нужно импортировать библиотеку SymPy. Она не поставляется вместе с Python по умолчанию, поэтому вы должны установить её в своей системе, иначе код не будет работать.

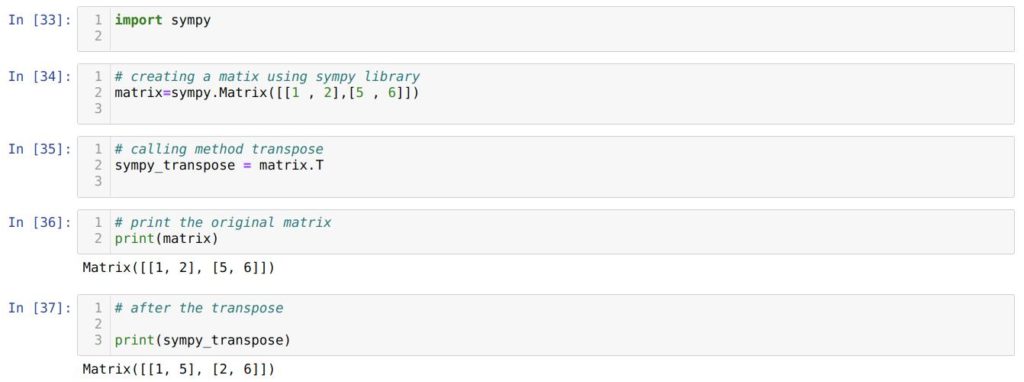
В ячейке номер [34] мы создаем матрицу с помощью библиотеки sympy.

Дальше, в ячейке [35], мы вызываем transpose (T) при помощи точечного оператора и сохраняем результаты в новую переменную sympy_transpose .

В ячейке номер [36] мы печатаем исходную матрицу matrix . А в ячейке номер [37] – транспонированную матрицу sympy_transpose . Как видим, у нас получилась транспонированная матрица.

Метод 4. Транспонирование матрицы с использованием вложенного цикла

В Python матрицу можно транспонировать и без применения каких-либо библиотек. Для этого нам придется использовать вложенные циклы.

Мы создаем одну матрицу, а затем вторую (того же размера, что и первая) — для сохранения результатов после транспонирования. При этом важно отметить, что мы далеко не всегда знаем размерность исходной матрицы. Поэтому матрицу для результата мы создаем не напрямую, а используя размер исходной.

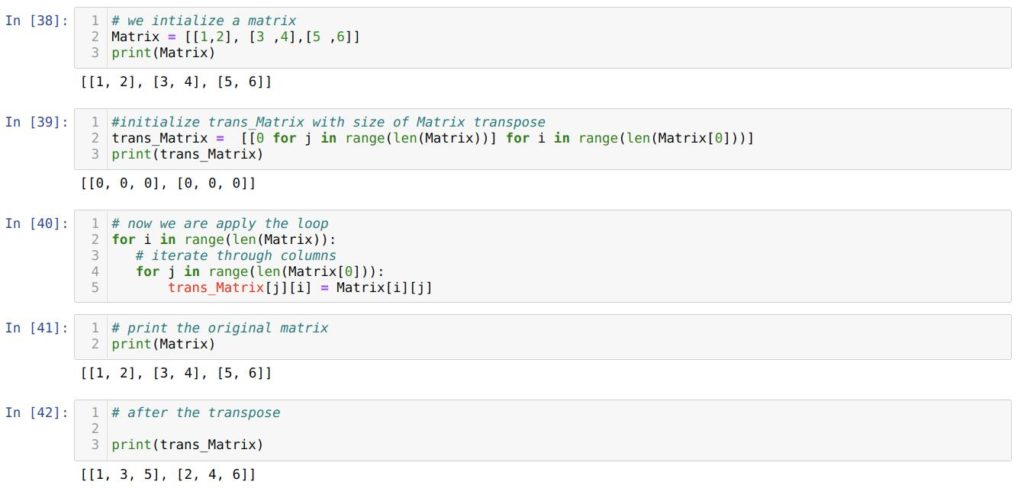
В ячейке номер [38] мы создаем матрицу и выводим ее на экран.

В следующей ячейке мы применяем «питонический» способ узнать размерность транспонированной матрицы, используя исходную. А именно — используем генератор списков со вложенными циклами for .

В ячейке [40] мы запускаем два цикла for . Внешний цикл предназначен для строк, а вложенный – для столбцов.

В ячейке номер [41] мы выводим исходную матрицу Matrix . А в ячейке [42] — транспонированную матрицу trans_Matrix .

Метод 5. Использование генератора списка

Следующий метод, который мы разберем, — это использование генератора списка. Этот метод похож на предыдущий с использованием вложенных циклов, но он более «питонический». Можно сказать, что это более продвинутый способ транспонирования матрицы в одной строке кода без использования библиотек.

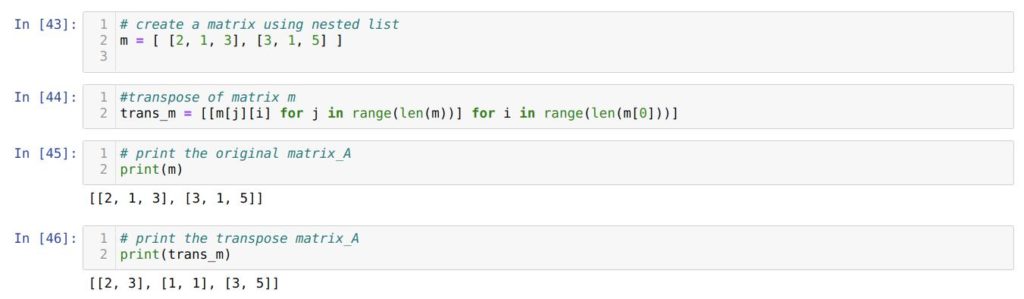
Сначала мы создаем матрицу m , используя вложенные списки.

Затем в ячейке номер [44] мы используем вложенные циклы, как и в предыдущем примере. Однако здесь мы делаем это в одну строчку, используя генератор списков. Более того, тут нет никакой необходимости менять индексы [j] [i] местами, как мы это делали в предыдущий раз.

В следующей ячейке мы выводим исходную матрицу m . После этого в ячейке номер [42] выводим транспонированную матрицу trans_m . Как видим, желаемый результат получен.

Метод 6. Транспонирование матрицы с помощью pymatrix

Pymatrix – ещё одна облегченная библиотека для матричных операций в Python. Мы можем выполнить транспонирование и с её помощью.

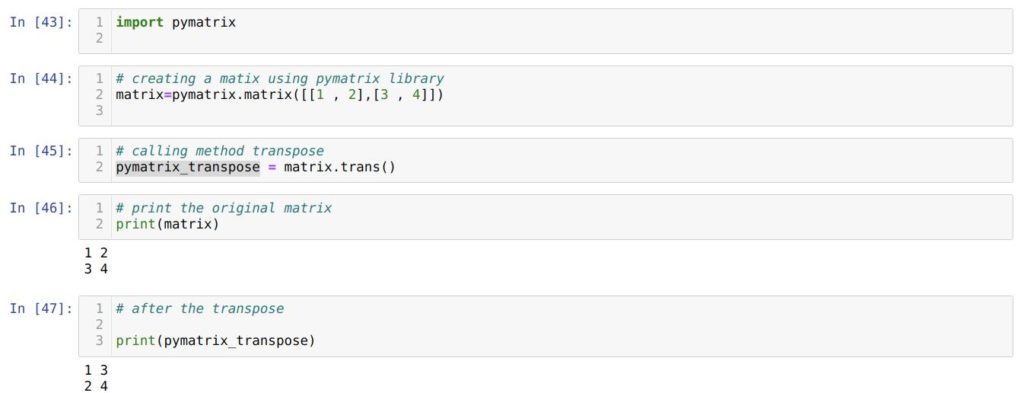
В ячейке номер [43] мы импортируем библиотеку pymatrix. Она не поставляется вместе с Python по умолчанию, поэтому, чтобы код работал корректно, нужно установить ее в своей системе перед использованием.

Затем при помощи библиотеки pymatrix мы создаем матрицу (в ячейке [44]).

В ячейке номер [45] вызываем метод trans() для нашей матрицы и сохраняем результаты в новую переменную pymatrix_transpose.

Потом мы выводим на экран исходную матрицу matrix . А в ячейке номер [47] выводим уже транспонированную матрицу pymatrix_transpose . Как видим, код отработал правильно.

Метод 7. Использование метода zip

Zip – еще один метод транспонирования матрицы.

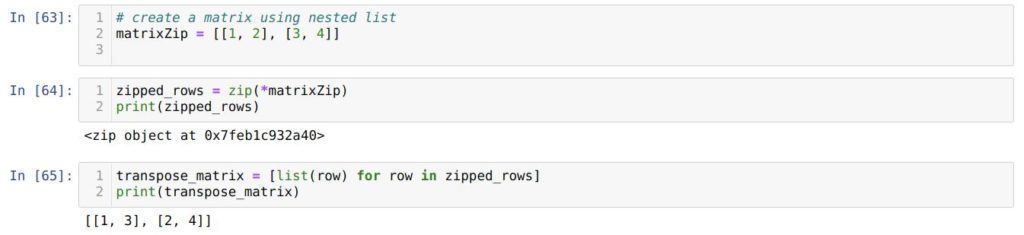
В ячейке номер [63] мы создаем новую матрицу, используя вложенные списки.

В ячейке номер [64] мы передаем матрицу в zip с помощью оператора * . Мы вызываем каждую строку, а затем преобразуем эту строку в новый список, который становится транспонированной матрицей.

Заключение

Итак, сегодня мы рассмотрели, как транспонировать матрицу в Python. Мы разобрали различные методы, которые могут помочь нам в транспонировании матрицы (с использованием библиотек и без них).

Мы также познакомились с несколькими новыми библиотеками, такими как pymatrix и sympy.

Надеемся, теперь у вас не осталось вопросов о том, как транспонировать матрицу. Более того, вы можете выбрать наиболее подходящий способ для решения этой задачи.

Источник