Time series linear regression python

Linear Regression on Time Series with SciKit Learn and Pandas

This post demonstrates simple linear regression from time series data using scikit learn and pandas.

Imports

Import required libraries like so.

import numpy as np import pandas as pd import datetime from sklearn import linear_model 

Create time series data

There are many ways to do this. Refer to the Time series section in the pandas documentation for more details. Here, we take a date range for the year of 2020 and create a datetime index based on each day.

start = datetime.datetime(2020, 1, 1) end = datetime.datetime(2020, 12, 31) index = pd.date_range(start, end) index, len(index) 

(DatetimeIndex(['2020-01-01', '2020-01-02', '2020-01-03', '2020-01-04', '2020-01-05', '2020-01-06', '2020-01-07', '2020-01-08', '2020-01-09', '2020-01-10', . '2020-12-22', '2020-12-23', '2020-12-24', '2020-12-25', '2020-12-26', '2020-12-27', '2020-12-28', '2020-12-29', '2020-12-30', '2020-12-31'], dtype='datetime64[ns]', length=366, freq='D'), 366) 

Create a pandas dataframe

Next, we can put this in a pandas dataframe. We can add an artificial “value” column that is a multiple of 5 for some generic target data.

multiple = 5 l = list(range(0, len(index)*multiple, multiple)) df = pd.DataFrame(l, index = index) df.index.name = "date" df.columns = ["value"] df 

 value date 2020-01-01 0 2020-01-02 5 2020-01-03 10 2020-01-04 15 2020-01-05 20 . . 2020-12-27 1805 2020-12-28 1810 2020-12-29 1815 2020-12-30 1820 2020-12-31 1825 366 rows × 1 columns 

Simple feature engineering from time series

We want something sensible to predict from. One simple option is to convert the date index into an integer from the minimum start date like so:

df['days_from_start'] = (df.index - df.index[0]).days; df 

value days_from_start date 2020-01-01 0 0 2020-01-02 5 1 2020-01-03 10 2 2020-01-04 15 3 2020-01-05 20 4 . . . 2020-12-27 1805 361 2020-12-28 1810 362 2020-12-29 1815 363 2020-12-30 1820 364 2020-12-31 1825 365 366 rows × 2 columns 

Simple Regression

We can now pull out the columns for simple linear regression.

x = df['days_from_start'].values.reshape(-1, 1) y = df['value'].values 

Note that our input variables x have to be reshaped for input to the model.

Use scikit’s LinearRegression to fit the model

model = linear_model.LinearRegression().fit(x, y) linear_model.LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False) LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False) model.predict([[1], [7], [50]]) 

More

Источник

Time series linear regression python

Introduction

Linear regression is always a handy option to linearly predict data. At first glance, linear regression with python seems very easy. If you use pandas to handle your data, you know that, pandas treat date default as datetime object. The datetime object cannot be used as numeric variable for regression analysis. So, whatever regression we apply, we have to keep in mind that, datetime object cannot be used as numeric value. The idea to avoid this situation is to make the datetime object as numeric value. Then do the regression. During plotting the regression and actual data together, make a common format for the date for both set of data. In this case, I have made the data for x axis as datetime object for both actual and regression value.

Importing Packages

import pandas as pd import numpy as np import scipy.stats as sp import matplotlib.pyplot as plt %matplotlib inline

The pandas library is imported for data handling. Numpy for array handling. Os for file directory. SciPy for linear regression. Matplotlib for plotting. However, the last line of the package importing block (%matplotlib inline) is not necessary for standalone python script. This line is only useful for those who use jupyter notebook. Now let us start linear regression in python using pandas and other simple popular library.

Importing data

df = pd.read_excel('data.xlsx') df.set_index('Date', inplace=True)

Set your folder directory of your data file in the ‘binpath’ variable. My data file name is ‘data.xlsx’. It has the time series Arsenic concentration data. Pandas ‘read_excel’ function imports all data. If your data is in another format, there are various other functions available in pandas library. We should make the ‘Date’ column as index column. For time series data it is very important to make the index column as date.

Viewing the data

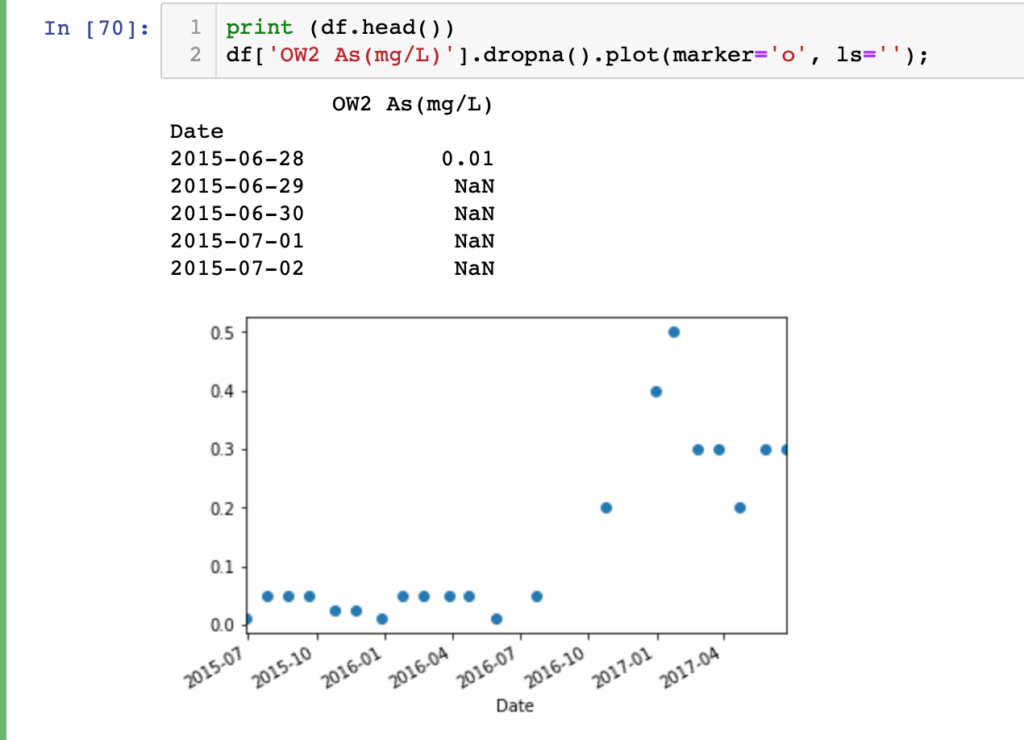
print (df.head()) df['OW2 As(mg/L)'].dropna().plot(marker='o', ls='');

For initial impression we should view the data to check whether everything is ok with the data or not. As you can see, in my data set there are a lot of empty cells. Pandas imports empty cells as NaN. So, before any kind of analysis or plotting we should keep this in mind.

Linear Regression

y=np.array(df['OW2 As(mg/L)'].dropna().values, dtype=float) x=np.array(pd.to_datetime(df['OW2 As(mg/L)'].dropna()).index.values, dtype=float) slope, intercept, r_value, p_value, std_err =sp.linregress(x,y) xf = np.linspace(min(x),max(x),100) xf1 = xf.copy() xf1 = pd.to_datetime(xf1) yf = (slope*xf)+intercept print('r = ', r_value, '\n', 'p = ', p_value, '\n', 's = ', std_err)

To start with the linear regression, ‘y’ variable represents all Arsenic concentration data without NaN values. Corresponding dates are saved in ‘x’ variable. All dates are passed through pandas ‘to_datetime()’ function to convert it to float numeric for the regression purpose. By default the time origin is ‘unix’ based and the datetime object will be saved in ‘nanosecond’ unit. Now our xy data are ready to pass through the linear regression analysis. We will use ‘linregress’ function from SciPy statistics package for the linear regression. The final output from linear regression are saved in slop, intercept, r_value, p_value, std_err varibles. Now we will predict some y values within our data range. We will also save the unix numeric date values in different variables as datetime object. As our actual data set’s date are in datetime object format.

Data visualisation

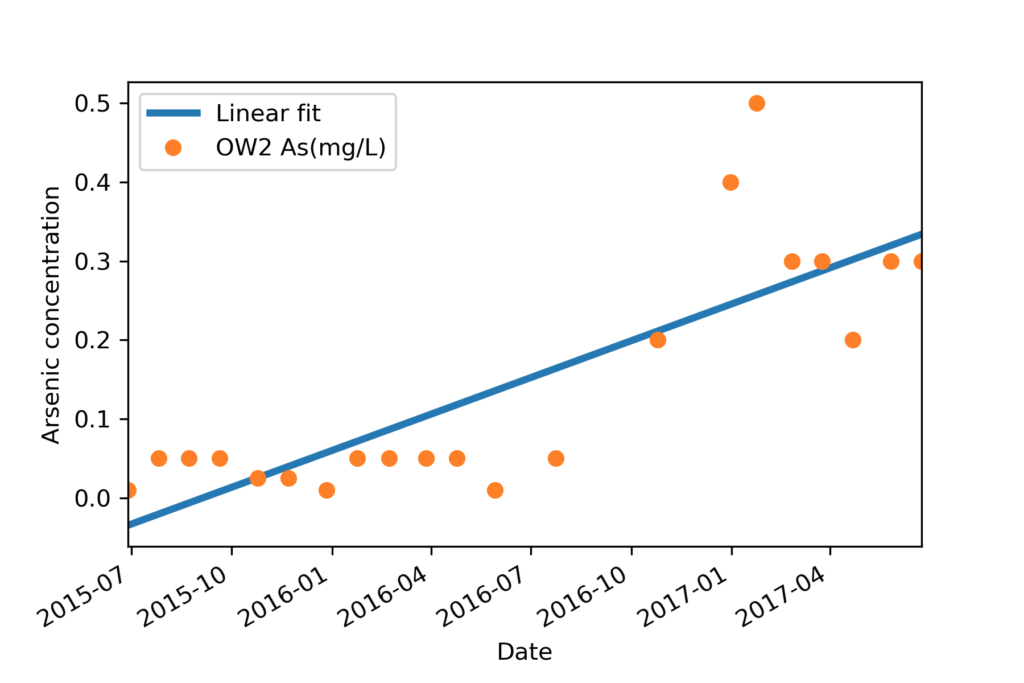
f, ax = plt.subplots(1, 1) ax.plot(xf1, yf,label='Linear fit', lw=3) df['OW2 As(mg/L)'].dropna().plot(ax=ax,marker='o', ls='') plt.ylabel('Arsenic concentration') ax.legend();

Now all our data and predicted data sets are ready to plot in same date time axis. Visualisation will look like the image name ‘Final plot’.

For data analysis you can checkout my fiverr gig. The link goes below.

Источник

How To Model Time Series Data With Linear Regression

Welcome back! This is the 4th post in the column to explore analysing and modeling time series data with Python code. In the previous three posts, we have covered fundamental statistical concepts, analysis of a single time series variable, and analysis of multiple time series variables. From this post onwards, we will make a step further to explore modeling time series data using linear regression.

1. Ordinary Least Squares (OLS)

We all learnt linear regression in school, and the concept of linear regression seems quite simple. Given a scatter plot of the dependent variable y versus the independent variable x, we can find a line that fits the data well. But wait a moment, how can we measure whether a line fits the data well or not? We cannot just visualize the plot and say a certain line fits the data better than the other lines, because different people may make different evaluation decisions. How can we quantify the evaluation?

Ordinary least squares (OLS) is a method to quantify the evaluation of the different regression lines. According to OLS, we should choose the regression line that minimizes the sum of the squares of the differences between the observed dependent variable and the predicted dependent variable.

2. Gauss-Marcov Assumptions

We can find a line that best fits the observed data according to the evaluation standard of OLS. A general format of the line is:

Here, μᵢ is the residual term that is the part of yᵢ that cannot be explained by xᵢ. We can find this best regression line according to OLS requirement, but are we sure OLS generates the best estimator? One example is when there is an outlier, the ‘best’ regression line calculated according to OLS obviously does not fit the observed data well.

Источник