Теория принятия решений метод динамического программирования

Методы теории массового обслуживания

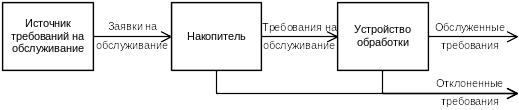
Система массового обслуживания – это модель некоторой реальной системы, в которой имеется случайный поток требований на обслуживание, которое ведется в системе с некоторыми определенными правилами. Теория массового обслуживания имеет своей целью разработку методов и моделей оценивания эффективности процессов массового обслуживания и качества реализующих их систем, а также моделей и методов организации данных процессов и систем, обеспечивающих требуемую их эффективность и качество [10]. На рис. 25 в качестве примера приведен один из простейших вариантов таких систем.

Задачи разработки управленческого решения, решаемые методами теории массового обслуживания, относятся к категории задач в условиях риска, а основным методом решения подобных задач можно считать метод Монте-Карло. Оптимизация принимаемых решений на основе использования теории массового обслуживания может вестись, в частности, за счет выбора количества устройств обработки требований на обслуживание.

Рис. 24. Сетевой график, выдаваемый системой управления проектами

Рис. 25. Пример одноканальной системы массового обслуживания

Метод динамического программирования

Динамическим программированием называется метод оптимизации, в котором процесс принятия решения может быть разбит на шаги [11]. Каждый шаг переводит объект управления из состояния в состояние посредством управления . Если общее количество шагов равно , то можно говорить о последовательности состояний системы, которую она принимает в результате воздействия различных управлений Целевая функция системы зависит от начального состояния и управления

Предполагается, что состояние системы в конце -того шага зависит только от предшествующего состояния и управления на -том шаге . Тогда уравнение состояния системы имеет вид

Если считать целевую функцию аддитивной от показателя эффективности каждого шага, то на шаге и целевая функция имеет вид

Решением задачи динамического программирования является определение такого управления , которое переводит систему из состояния в состояние при наибольшем (наименьшем) значении .

Для решения задачи динамического программирования был сформулирован так называемый принцип оптимальности. Его смысл которого сводится к следующему: каково бы ни было состояние системы в результате выполнения какого-либо числа шагов, управление на ближайшем шаге нужно выбирать так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к максимальному выигрышу на всех оставшихся шагах включая данный.

Рассмотрим последний шаг . Состояние системы к началу шага , управление, а — целевая функция. Согласно принципу оптимальности управление нужно выбирать так, чтобы для любого состояния получался условный максимум целевой функции

Решение , при котором достигается называется условным оптимальным управлением на шаге . Условный максимум целевой функции отыскивается для всех возможных состояний системы на последнем шаге. Далее рассматривается совместно последний и предпоследний шаг. Целевая функция в этом случае имеет вид

Отыскивается условное оптимальное управление на двух последних шагах для всех возможных состояний системы на предпоследнем шаге

Состояние системы при известном управлении определяется как , в связи с чем целевая функция зависит только от состояния на предыдущем шаге и текущего управления. Далее рассматривается три, четыре и т.д. последних шага. В общем случае для шага получается уравнение Белмана, впервые разработавшего метод динамического программирования.

В результате условной оптимизации могут быть получены последовательности значений критериальной функции и условных управлений

Решение задачи динамического программирования получается в результате подстановки конкретного значения в выражение для решения на первом шаге и . Далее определяется состояние первого шага

и так далее для всех шагов. Оптимальное решение задачи получается при последовательном расчете оптимальных решений и и новых состояний .

При практической реализации метода динамического программирования на ЭВМ возникает ряд трудностей, связанных, в частности, со способами описания состояния объекта управления. Как правило, рассматривается конечное число состояний объекта управления на каждом шаге. Тем не менее, наибольший интерес представляет случай отыскания оптимального состояния объекта из бесконечного числа возможных состояний, например, методом математического программирования. В доступной литературе такие материалы отсутствуют, кроме того, не имеется сведений о программной реализации метода динамического программирования, хотя потребность в решении таких задач в достаточно велика. Из сказанного следует, что доведение методов динамического программирования до практического использования представляет собой актуальную и важную задачу исследования.

Источник

6. Принятие решений на основе динамического программирования

Способ решения сложных задач путём разбиения их на более простые подзадачи. Он применим к задачам с оптимальной подструктурой , выглядящим как набор перекрывающихся подзадач, сложность которых чуть меньше исходной. В этом случае время вычислений, по сравнению с «наивными» методами, можно значительно сократить.

Оптимальная подструктура в динамическом программировании означает, что оптимальное решение подзадач меньшего размера может быть использовано для решения исходной задачи. К примеру, кратчайший путь в графе из одной вершины (обозначим s) в другую (обозначим t) может быть найден так: сначала считаем кратчайший путь из всех вершин, смежных с s, до t, а затем, учитывая веса ребер, которыми s соединена со смежными вершинами, выбираем лучший путь до t (через какую вершину лучше всего пойти). В общем случае мы можем решить задачу, в которой присутствует оптимальная подструктура, проделывая следующие три шага.

• Разбиение задачи на подзадачи меньшего размера.
• Нахождение оптимального решения подзадач рекурсивно, проделывая такой же трехшаговый алгоритм.
• Использование полученного решения подзадач для конструирования решения исходной задачи.

• перекрывающиеся подзадачи;
• оптимальная подструктура;
• возможность запоминания решения часто встречающихся подзадач.

• нисходящее динамическое программирование: задача разбивается на подзадачи меньшего размера, они решаются и затем комбинируются для решения исходной задачи. Используется запоминание для решений часто встречающихся подзадач.
• восходящее динамическое программирование: все подзадачи, которые впоследствии понадобятся для решения исходной задачи просчитываются заранее и затем используются для построения решения исходной задачи. Этот способ лучше нисходящего программирования в смысле размера необходимого стека и количества вызова функций, но иногда бывает нелегко заранее выяснить, решение каких подзадач нам потребуется в дальнейшем.

Источник

Теория принятия решений принятие оптимальных решений методами динамического программирования

1. Теория принятия решений принятие оптимальных решений методами динамического программирования

ТЕОРИЯ ПРИНЯТИЯ РЕШЕНИЙ
ПРИНЯТИЕ ОПТИМАЛЬНЫХ
РЕШЕНИЙ МЕТОДАМИ
ДИНАМИЧЕСКОГО
ПРОГРАММИРОВАНИЯ
Лекция 2.8

2. СОДЕРЖАНИЕ

Текущий контроль знаний
Часть 1. Общие принципы динамического
программирования.
Часть 2. Принятие решений на моделях,
сводимых к задачам дискретной оптимизации с
булевыми переменными.
Часть 3. Принятие решений на моделях,
сводимых к задачам дискретной оптимизации с
небулевыми переменными.
Часть 4. Принятие решений на моделях
оптимального упорядочения.

3. ТЕКУЩИЙ КОНТРОЛЬ ЗНАНИЙ

На бихроматическом графе G(X,U), │Х│= 8,│Х₁│=│Х₂│=4, матрица которого приведена
ниже, определить оптимальное распределение работ при условии, что:
1. Минимизируется время выполнения плана, при условии, что фонд зарплаты равен:
S= 4 ∙max.
2. Минимизируются затраты на выполнение плана при условии, что время его выполнения не
превышает величины Т= max.
3. Минимизируются затраты на выполнение плана при условии, что время его выполнения не
ограничено.
1
2
3
4
1
│k-5│;│k-15│
│k-10│;│k-25│
│k-7│;│k-17│
│k-8│;│k-15│
2
│k-3│;│k-30│
│k-25│;│k-15│
│k-2│;│k-19│
│k-4│;│k-32│
3
│k-31│;│k-15│
│k-6│;│k-14│
│k-3│;│k-35│
│k-23│;│k-25│
4
│k-16│;│k-14│
│k-35│;│k-5│
│k-11│;│k-10│
│k-5│;│k-15│

4. ЧАСТЬ 1

5. ОПРЕДЕЛЕНИЕ

Динамическое программирование
представляет собой многошаговый
процесс принятия решений,
направленных на достижение единой
цели. При этом на каждом шаге этого
процесса решается задача меньшей
размерности, чем исходная.

6. Принцип оптимальности Беллмана

Оптимальная стратегия обладает тем
свойством, что независимо от начального
состояния и начального решения задачи,
последующие решения должны составлять
оптимальную стратегию лишь в
рассматриваемый момент времени. Иными
словами оптимальная стратегия в каждый
момент времени определяется лишь
состоянием системы, но не ее предысторией.

7. Часть 2

8. ПРИМЕР 1: Решение задач с булевыми переменными

Задача о ранце:
6 x1 3 x2 4 x3 2 x4 max;
4 x1 6 x2 5 x3 5 x4 10; 1
i : x 1,0.
i
0
1
6,6
S
Первое число –
значение целевой
функции, второе –
ресурс.
1
0
10,1
0
9,0
8,1
1
1
10,1
6,6
6,6
0
0
6,6
3,4
0,10
1
9,0
1
0
-∞
-∞
0
1
2,5
1
4,5
0,10
x1
x2
x3
0
0
0,10
x4
0,10

9. САМОСТОЯТЕЛЬНО

Пользуясь методом динамического
программирования, решить задачу о ранце:
4 x1 7 x2 9 x3 3 x4 max;
6 x1 5 x2 8 x3 7 x4 12;
i : x 1,0.
i

10. ЧАСТЬ 3

11. ПРИМЕР 2: Решение задачи с небулевыми переменными

12. ПРИМЕР 2 (ПРОДОЛЖЕНИЕ)

13. Пример 2 (завершение)

14. САМОСТОЯТЕЛЬНО:

Решить задачу с небулевыми и с
булевыми переменными вида:
7 x1 2 x2 4 x3 5 x 4 max;
4 x 2 x 2 x 4 x 8;
1
2
3
4
i 3, xi ,
3 i 4 : xi .

15. Часть 4

16. ПРИМЕР 3: ЗАДАЧА КОММИВОЯЖЕРА

Решить, пользуясь методом динамического
программирования, разомкнутую задачу
коммивояжера, условия которой отвечают
графу G(X, U), изображенному на рисунке
ниже.
r (i, j ) z (i, j ) min;
i j
xs X : z (i, s ) 0; z ( s, j ) 1;
i
j
xt X : z (i, t ) 1; z (t , j ) 0;
i
j
x X \ ( x x ) : z (i, k ) z (k , j ) 1;
i
j
s
t
k
(i, j ) U : z (i, j ) 1,0.

17. ПРИМЕР 3. ХОД РЕШЕНИЯ

18. Самостоятельно вывести:

Формулы, определяющие:
1. Число вершин каждого слоя
построенной сети.
2. Число дуг, заходящих в каждую
вершину i-го слоя.
3. Число дуг, исходящих из каждой
вершины i-го слоя.

Источник